一)最长递增子序列:

300. 最长递增子序列 - 力扣（LeetCode）

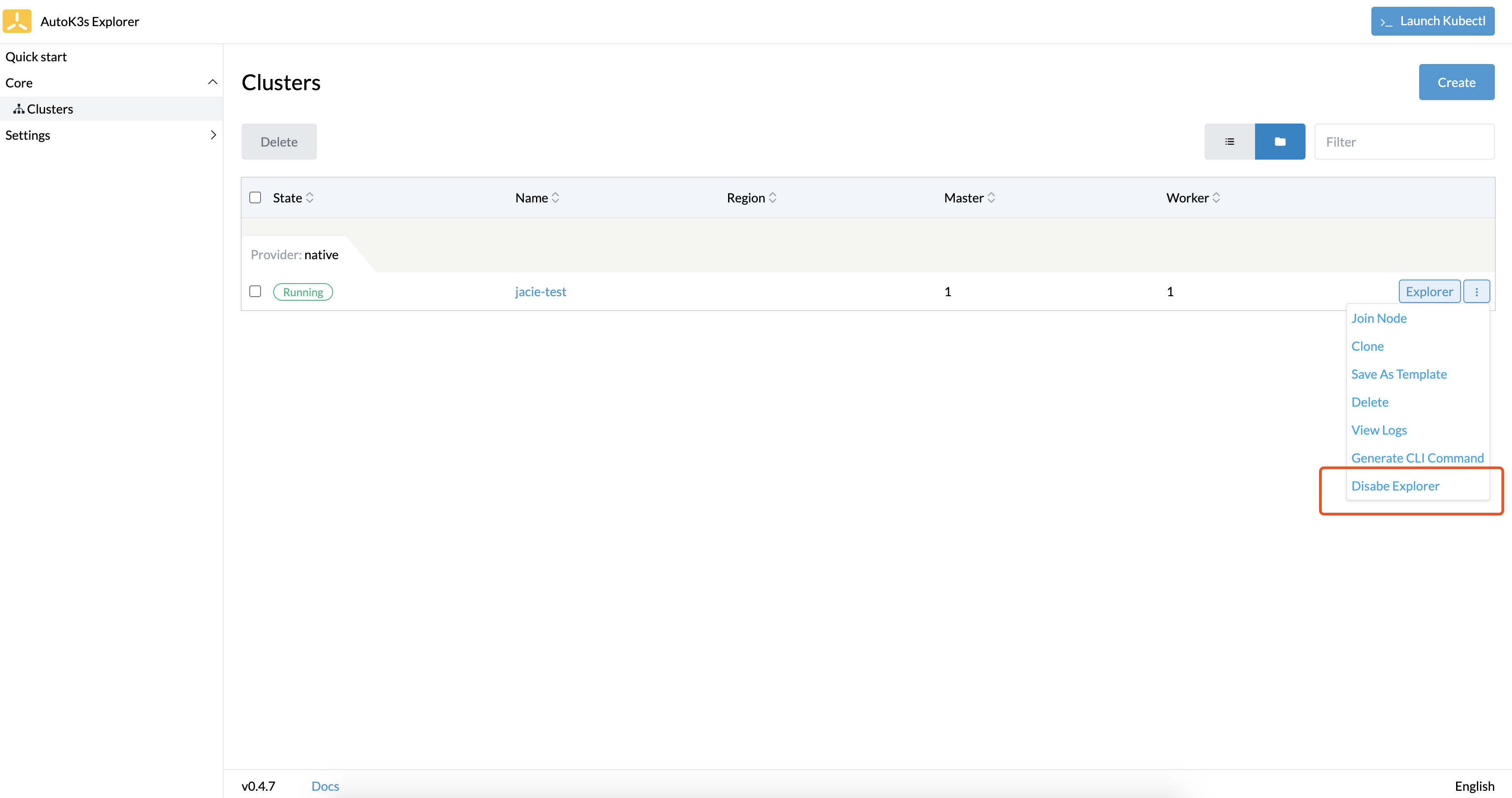
算法原理:

1.定义一个状态表示:经验+题目要求

dp[i]表示，以i位置为结尾，最长递增子序列的长度

中心思路就是找到以i位置为结尾的所有递增子序列，然后找到递增子序列中最长的一个子序列

2.根据状态表示推导状态转移方程

像子序列子数组这样的状态转移方程的推导，都是针对于如何构成这个子序列，或者是如何构成这个子数组，来划分问题的，同时以i位置为结尾的递增子序列，可以分成一下几类:

2.1)单独自己构成一个递增子序列，那么长度就是1

2.2)和前面的元素进行结合构成子序列:要么i位置的元素和i-1位置的元素进行结合成子序列

要么是和i-2位置的元素构成子序列，要么是和i-3位置的元素构成子序列

2.3)先找到以j位置为结尾的最长递增子序列的长度，并且array[i]>array[j]，然后再加上array[j]的值，就构成了以i为结尾的最长递增子序列

3.初始化+填表顺序:从左向右

对于长度问题的初始化，一般都是将dp表中的值初始化成元素最差的状态

4.返回值:返回dp表里面的最大值

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp=new int[nums.length];
        int maxlen=Integer.MIN_VALUE;
//1.单独一个元素就可以构成子序列
        for(int i=0;i<dp.length;i++){
            dp[i]=1;
        }
//2.j从0开始,j<=i进行遍历
        for(int i=0;i<nums.length;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]){
                   dp[i]=Math.max(dp[j]+1,dp[i]);
                }
            }
        maxlen=Math.max(dp[i],maxlen);
        }
    return maxlen;
    }
}

2)摆动序列:这个题和之前做的湍流子数组有点像

1)定义一个状态标识:

先找到以i位置元素为结尾的所有子序列中，再找到最长的摆动序列的长度

376. 摆动序列 - 力扣（LeetCode）

2)根据状态表示推导状态转移方程:

当以某一个位置为结尾的时候，最后呈现的趋势可能是下降的趋势也有可能是上升的趋势，所以说如果想以最后一个位置进行研究问题的话，是可以进行细分出两种状态的，要么是以下降状态到达最后一个位置，要么是以上升状态到达最后一个位置

1)f[i]表示以i位置元素为结尾的所有子序列中，最后一个位置呈现上升趋势的最长的摆动序列的长度

2)g[i]表示以i位置元素为结尾的所有子序列中，最后一个位置呈现下降趋势的最长的摆动序列的长度

3)像状态转移方程这类问题也就是子序列问题这样的分析，就是根据子序列的构成来进行分析的，就是来进行分析以i位置元素为结尾的所有子序列是如何来进行构成的

要么是单独自己一个元素来构成子序列，那么这个子序列就是本身，要么就是跟着i元素前面的一个元素后面来充当子序列，长度大于1

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int f[]=new int[nums.length];
        int g[]=new int[nums.length];
        for(int i=0;i<nums.length;i++){
            f[i]=1;
            g[i]=1;
        }
        int maxlen=Integer.MIN_VALUE;
        for(int i=0;i<nums.length;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]){
                    f[i]=Math.max(f[i],g[j]+1);
                }
                if(nums[i]<nums[j]){
                    g[i]=Math.max(g[i],f[j]+1);
                }
            }
            maxlen=Math.max(f[i],maxlen);
            maxlen=Math.max(g[i],maxlen);
        }
    return maxlen;
    }
}

三)最长递增子序列的个数: