文章目录
- 1. 两数之和
- 2. 四数相加II
- 3. 赎金信
- 4. 三数之和
- 5. 四数之和
1. 两数之和
1. 两数之和
虽然是LeetCode第一题,但是还是挺难的!

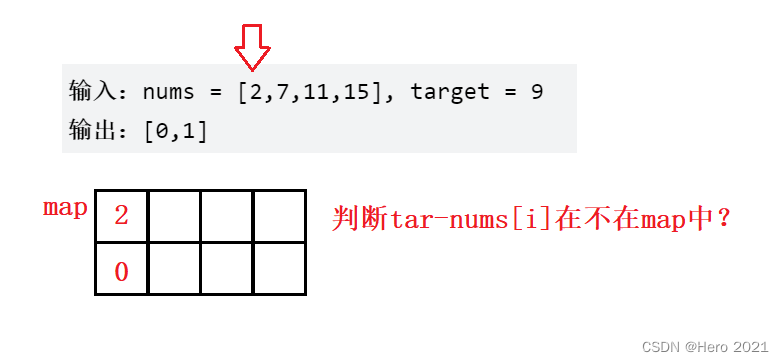
模拟一下:
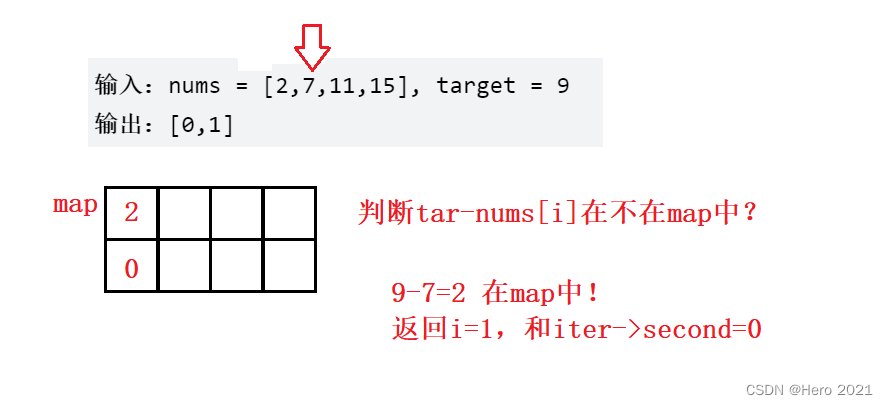
class Solution
{
public:
vector<int> twoSum(vector<int> &nums, int tar)
{
unordered_map<int, int> m;
for (int i = 0; i < nums.size(); i++)
{
auto iter = m.find(tar - nums[i]);
if (iter != m.end())
{
return {iter->second, i};
}
else
{
m.insert({nums[i], i});
}
}
return {};
}
};
1、为啥想到用哈西法?
因为我们在遍历nums数组的时候,我们要存放之前已经遍历过的元素(方便查询),若之前遍历过,那么就找到了一对数,满足要求。
2、为啥想到用map?
因为set只能存放key,但是我们这里还想要知道元素对应的下标,所以选取map,因为要查询效率更高,所以选取unordered_map。
2. 四数相加II
454.四数相加II
暴力解法就是4层for循环。
采用两两分组,这样循环的话,优化到了O(N2),这样和上一题的解法就差不多了。
定义一个unordered_map,key放a和b两数之和,value放a和b两数之和出现的次数,再遍历大C和大D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
class Solution
{
public:
int fourSumCount(vector<int> &A, vector<int> &B, vector<int> &C, vector<int> &D)
{
unordered_map<int, int> map; // key存a+b值 val存a+b出现的次数
for (int a : A)
{
for (int b : B)
{
map[a + b]++;
}
}
int count = 0;
for (int c : C)
{
for (int d : D)
{
if (map.find(0 - (c + d)) != map.end())
{
count += map[0 - (c + d)];
}
}
}
return count;
}
};
3. 赎金信
很像,242.有效的字母异位词
class Solution
{
public:
bool canConstruct(string ransomNote, string magazine)
{
if (ransomNote.size() > magazine.size())
return false;
int hash[26] = {0}; // 题目给出都是小写字母
for (int i = 0; i < magazine.size(); i++)
{
hash[magazine[i] - 'a']++;
}
for (int i = 0; i < ransomNote.size(); i++)
{
hash[ransomNote[i] - 'a']--;
if (hash[ransomNote[i] - 'a'] < 0)
{
return false;
}
}
return true;
}
};
4. 三数之和
15.三数之和
利用双指针法
class Solution
{
public:
vector<vector<int>> threeSum(vector<int> &nums)
{
sort(nums.begin(), nums.end());
vector<vector<int>> res;
for (int i = 0; i < nums.size(); i++)
{
if (nums[i] > 0)
return res;
// 对于a去重 用nums[i] == nums[i - 1]?不用nums[i] == nums[i + 1]
if (i > 0 && nums[i] == nums[i - 1])
continue;
int left = i + 1;
int right = nums.size() - 1;
while (left < right) // 为啥不能left<=right?
{
if (nums[i] + nums[left] + nums[right] > 0)
right--;
else if (nums[i] + nums[left] + nums[right] < 0)
left++;
else
{
res.push_back({nums[i], nums[left], nums[right]});
// 对于 b、c 去重!
// 去重b、c要放在这里,因为我们要至少收获一个结果集
while (left < right && nums[left] == nums[left + 1])
left++;
while (left < right && nums[right] == nums[right - 1])
right--;
// 找到答案时,双指针同时收缩
left++;
right--;
}
}
}
return res;
}
};
整体模拟:

使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
移动left 和right, 如果nums[i] + nums[left] + nums[right] > 0,right- -,如果nums[i] + nums[left] + nums[right] < 0,left++;直到等于0,把结果拿出来就好了。
1、为啥要排序?
因为题目要求不能有重复的三元组,这样能够不遗不漏。排序完后,方便后续指针的加减。
去重不是去掉nums中的元素,而是去掉相同的结果集,题目要求了结果集不能重复
2、[难点] 如何对a去重?为啥要nums[i] == nums[i-1]这样写?
直接跳过去就行了。
但是判断条件 nums[i] 与 nums[i + 1]是否相同,还是判断 nums[i] 与 nums[i-1] 是否相同呢,那就是选择nums[i] 与 nums[i-1],若选择nums[i]==nums[i+1]那就我们就把 三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据,当遍历到第一个-1 的时候,判断 下一个也是-1,那这组数据就pass了,本来这组数据是要算作结果的。
3、为啥要while(left<right) 不带等号?
0,0,0 的情况,可能直接导致 right<=left 了,从而漏掉了 0,0,0 这种三元组。
4、如何对b 、c去重?
也是一样的道理:
while (right > left && nums[right] = nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
5. 四数之和
18.四数之和
一定要先做三数之和。
这个题和三数之和的逻辑差不多,都可以使用双指针法。
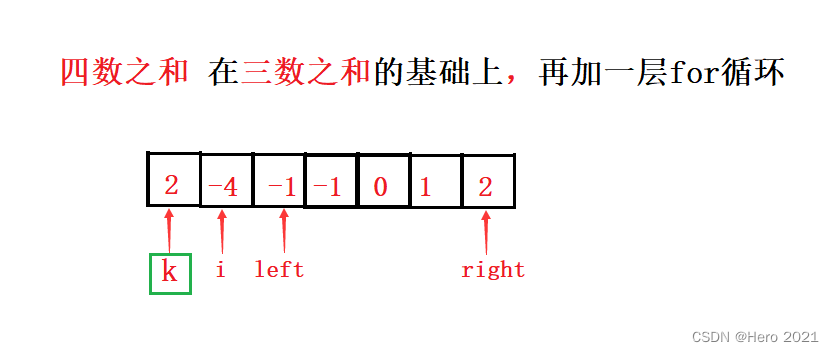
class Solution
{
public:
vector<vector<int>> fourSum(vector<int> &nums, int tar)
{
vector<vector<int>> res;
sort(nums.begin(), nums.end());
for (int k = 0; k < nums.size(); k++)
{
// 一级剪枝
if (nums[k] > tar && nums[k] >= 0)
{
break;
}
// 一级去重:对于nums[k]去重
if (k > 0 && nums[k] == nums[k - 1])
{
continue;
}
// 三数之和的逻辑
for (int i = k + 1; i < nums.size(); i++)
{
// 二级剪枝
if (nums[k] + nums[i] > tar && nums[k] + nums[i] >= 0)
{
break;
}
// 二级去重:对于nums[i]去重
if (i > k + 1 && nums[i] == nums[i - 1])
{
continue;
}
int left = i + 1;
int right = nums.size() - 1;
while (left < right)
{
if ((long)nums[k] + nums[i] + nums[left] + nums[right] > tar)
right--;
else if ((long)nums[k] + nums[i] + nums[left] + nums[right] < tar)
left++;
else
{
res.push_back(vector<int>{nums[k], nums[i], nums[left], nums[right]});
// 对于left 和 right 再进行去重
while (left < right && nums[left] == nums[left + 1])
left++;
while (left < right && nums[right] == nums[right - 1])
right--;
left++;
right--;
}
}
}
}
return res;
}
};
1、一级剪枝
if (nums[k] > tar && nums[k] >= 0)
{
break;
}
2、一级去重,nums[k]去重
if (k > 0 && nums[k] == nums[k - 1])
{
continue;
}
3、二级剪枝处理
nums[k] + nums[i]看做一个整体,然后再去移动left和right进行缩小判断。
4、二级去重,nums[i]去重
一样的道理。