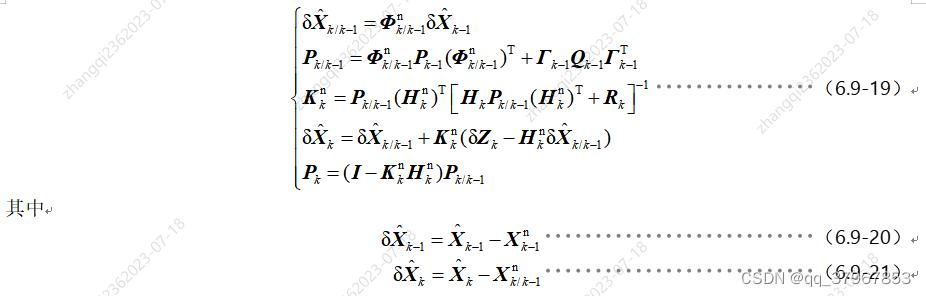1.卡尔曼的推导：

1）先看系统随机系统状态空间模型：（线性）
所谓线性是指递推或者状态转移方程是线性的
至于参数解释自己去看书，本文旨在捋顺推导思路。
2）k-1时刻值减去k-1的状态最优估计=k-1时刻状态估计误差。首先计算k-1时刻状态估计误差（参考值与估计值之间偏差）：

3）根据k-1时刻最优状态估计和系统状态方程可对k时刻（当前时刻）的状态做最优估计（最优一步预测）：

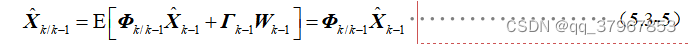
4）计算状态一步预测误差为：

5）把1）式和3）式带入4）式，结合2）式得：

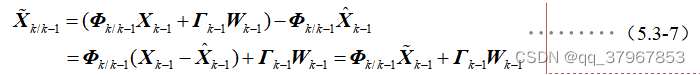
此刻状态一步预测误差计算好了，那么可以计算状态一步预测均方误差阵：

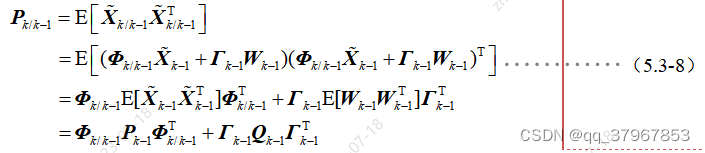
而k-1时刻状态估计误差阵为：

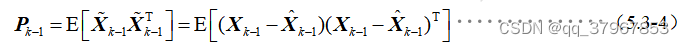
同理计算量测：
1）通过状态一步预测和系统的量测方程可对时刻的量测作一步预测：

2）量测一步预测误差公式为：

3）将系统式和1）式带入2）得量测一步预测误差：
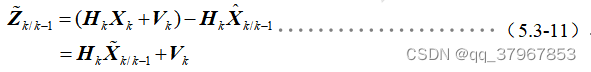量4）计算量测一步预测均方误差阵、状态一步预测与量测一步预测之间的协均方误差阵：

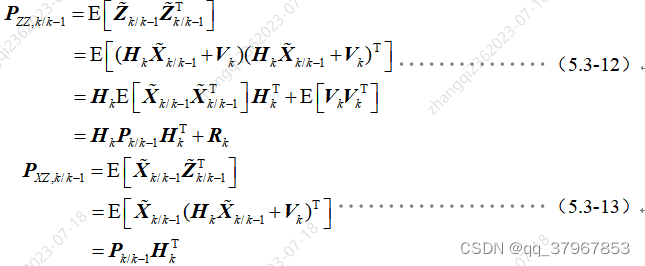
至此可以做到利用系统状态方程的状态一步预测去估计当前时刻的值，但由于没有用到量测方程的任何信息，会导致估计精度不高。又因为量测一步预测误差中包含状态一步预测的信息，因此综合考虑，利用量测一步预测误差修正当前状态估计作为最终的最优状态估计：

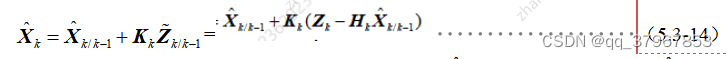
5）对上式进行化简：

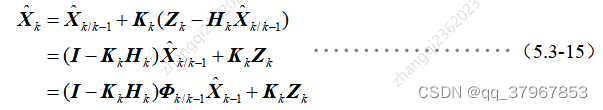
可以看到当前状态估计是前一时刻状态估计和当前量测的线性组合（加权估计），利用量测误差对先验估计进行修正得到后验估计。
接下来求取K以使得后验估计误差（当前时刻状态估计误差）最小：
6）当前k时刻状态估计误差为：

7）将上面5）式带入6）得：

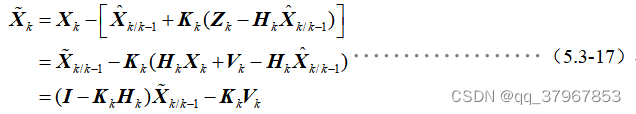
8）同理求k时刻（当前时刻）状态估计的均方误差阵：

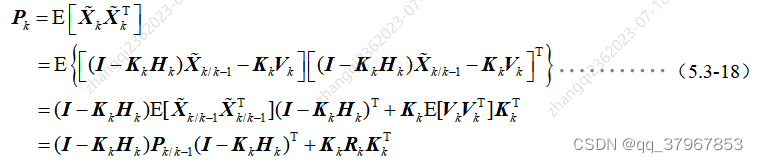
9）估计误差是一随机向量，使其“误差最小”的含义规定为使各分量的均方误差之和最小，即

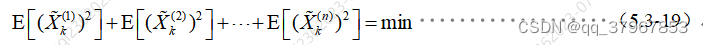
等价于：


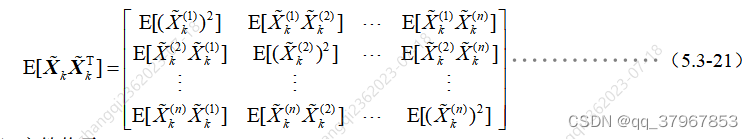
10）因为均方误差阵必定是对称阵，因此8）式可展开为：

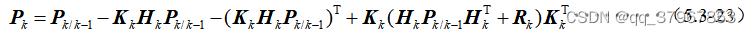
11）对10）式两边同时求迹运算，得：

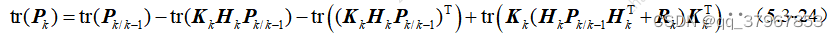
上式是关于待定参数矩阵K的二次函数，所以tr§必定存在极值（按概率含义这里应当是极小值）。
为了便于利用求导方法求取上式的极值，引入方阵的迹对矩阵求导的两个等式，分别如下：


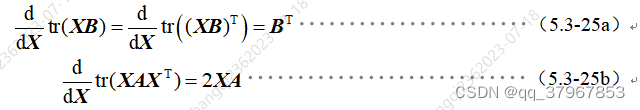
两边同时对K求导：

根据函数极值解得：

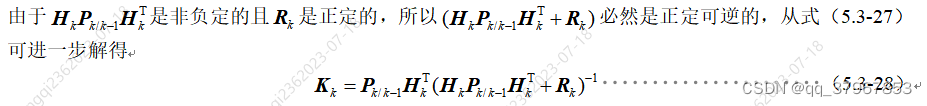
也就是当K等于以上取值时，当前状态估计误差最小。此时，将上式带入10）式得k时刻均方根误差阵为：

至此推导出卡尔曼滤波五个公式：

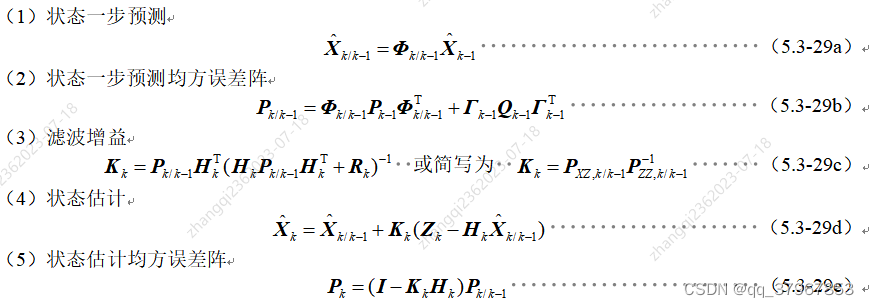
2.扩展卡尔曼推导：

1）先看系统随机系统状态空间模型：（非线性）


与卡尔曼唯一不同就是扩展卡尔曼是处理非线性模型，因此需要对状态转移方程(无论预测还是量测)都需要进行一节泰勒展开得到雅可比矩阵，以此来进行线性化。
1）同理求k-1时刻状态估计：

2）根据k-1时刻最优状态估计和系统状态方程可对k时刻（当前时刻）的状态做最优估计（最优一步预测）：

3）计算状态一步预测误差为：

在卡尔曼推导中，这一步是直接带入系统方程，但在这里需要先进行线性化：

同理求量测：


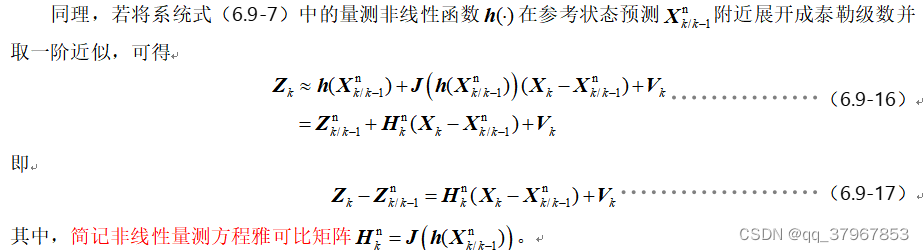
因此可以改写原非线性系统为线性系统：

改写5个公式：