卷积

如果将图片从 $H\ast W\ast C$ 拉伸到 $N\ast 1$ 的维度，而参数矩阵又是 $N\ast M$ 的大小。N很大，M也很大。整个网络中的参数量会变得巨大。

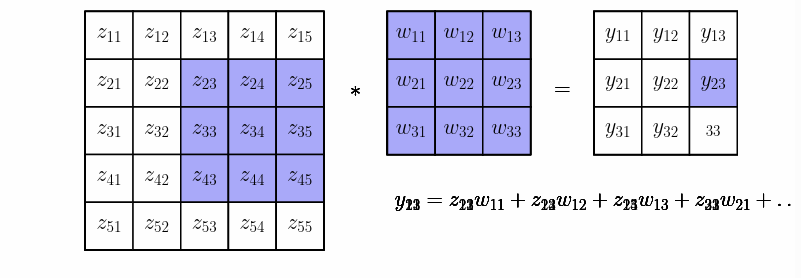
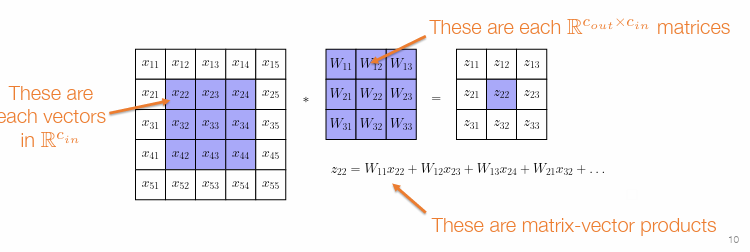
卷积过程，使用一个filter 在整个图片上滑动。
当然输入的图象可能有多个channel，输出的图象也可以有更多的channel

Padding 填充

当卷积完成之后，会发现输出图像的 H W 高和宽都小了一圈。
这时我们需要进行填充。一般都是填充0.
如果卷积核的大小是奇数的k，那么在图像周围一圈填充的宽度是 (k-1)/2

Strided Convolutions / Pooling 步幅卷积池化

用于对输入数据进行下采样，有助于减少网络的计算复杂度并提高其对新数据的泛化能力。

Pooling

池化是将输入分成非重叠的区域，并在每个区域内取最大值或平均值。

步幅卷积

使得卷积核以大于一的步幅在图像上进行滑动。

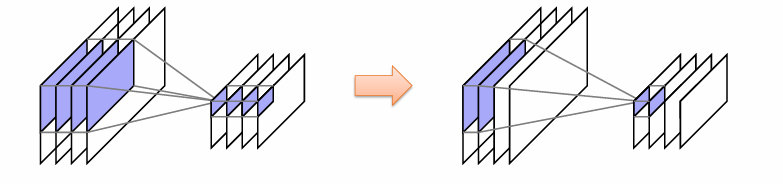
Grouped Convolutions 分组卷积

如果输入、输出的channel数依然很大，会导致卷积核中的参数依然很多。会导致过拟合并且降低计算速度。

使用分组卷积，将输出的channel和输入的channel都分组。 对应分组的输出channel只和对应的分组的输入channel相关。

Dilations

扩张卷积（Dilated Convolution），也称为空洞卷积（Atrous Convolution），是一种在卷积神经网络中常用的操作。它可以增加卷积神经网络的有效感受野（Effective Receptive Field），从而扩大网络的感受野范围，以提高网络对全局信息的感知能力。

但是如果使用扩张卷积，想要输入和输出得到相同的大小，必须增加更多的填充。

卷积的微分操作

定义卷积操作
$$z=conv(x,W)$$
在进行反省传播时，我们需要计算伴随矩阵

$$\bar{v}\frac{\partial conv(x,W)}{\partial W},\bar{v}\frac{\partial conv(x,W)}{\partial x}$$

考虑对于简单矩阵乘法运算

$$z=Wx$$
$$\frac{\partial z}{\partial x}=W$$
得到伴随矩阵 ${▽}_{x}y=W^{T}v$

当向下游传递的时候，我们只需要计算$W^T$,便可以计算梯度。

对于卷积操作又该怎么求 $W^T$

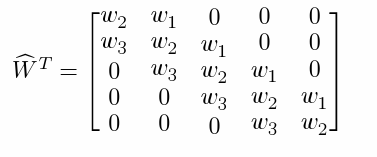
当我们计算梯度伴随的时候，向下游传递的值为 ${\hat{W}}^{T}v$ ，相当于将卷积核反转进行卷积。

对卷积操作求梯度，相当于上游梯度 v 与 卷积核W的反转进行卷积。

$\bar{v}\frac{\partial conv(x,W)}{\partial W}$ 这个情况怎么求？

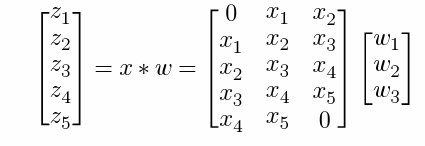
将x展开成上面的式子的情况，可以使用 im2col 函数进行操作。