1. 自动求导

在深度学习中，我们通常需要训练一个模型来最小化损失函数。这个过程可以通过梯度下降等优化算法来实现。梯度是函数在某一点上的变化率，可以告诉我们如何调整模型的参数以使损失函数最小化。自动求导是一种计算梯度的技术，它允许我们在定义模型时不需要手动推导梯度计算公式。PyTorch 提供了自动求导的功能，使得梯度的计算变得非常简单和高效。

PyTorch是动态图，即计算图的搭建和运算是同时的，随时可以输出结果。在pytorch的计算图里只有两种元素：数据（tensor）和运算（operation）。

运算包括了：加减乘除、开方、幂指对、三角函数等可求导运算。

数据可分为：叶子节点（leaf node）和非叶子节点；叶子节点是用户创建的节点，不依赖其它节点；它们表现出来的区别在于反向传播结束之后，非叶子节点的梯度会被释放掉，只保留叶子节点的梯度，这样就节省了内存。如果想要保留非叶子节点的梯度，可以使用retain_grad()方法。

torch.tensor 具有如下属性：

查看是否可以求导 requires_grad
查看运算名称 grad_fn
查看是否为叶子节点 is_leaf
查看导数值 grad

针对requires_grad属性，自己定义的叶子节点默认为False，而非叶子节点默认为True，神经网络中的权重默认为True。判断哪些节点是True/False的一个原则就是从你需要求导的叶子节点到loss节点之间是一条可求导的通路。当我们想要对某个Tensor变量求梯度时，需要先指定requires_grad属性为True，指定方式主要有两种：

x = torch.tensor(1.).requires_grad_() # 第一种

x = torch.tensor(1., requires_grad=True) # 第二种

总结：

（1）torch.tensor()设置requires_grad关键字参数

（2）查看tensor是否可导，x.requires_grad 属性

（3）设置叶子变量 leaf variable的可导性，x.requires_grad_()方法

（4）自动求导方法 y.backward() ，直接调用backward()方法，只会计算对计算图叶节点的导数。

（5）查看求得的到数值， x.grad 属性

1.1 梯度计算

自动求导的核心是反向传播算法（Backpropagation）。反向传播算法是一种高效地计算梯度的方法，它使用链式法则计算每个可导操作的梯度，然后利用这些梯度更新参数。一旦我们创建了可导张量，PyTorch 将会自动追踪所有涉及这些张量的操作，并构建一个计算图。计算图是一个有向无环图，表示了计算过程中张量之间的依赖关系。

1.1.1 一阶导数

然后我们举个例子：z=w*x+b

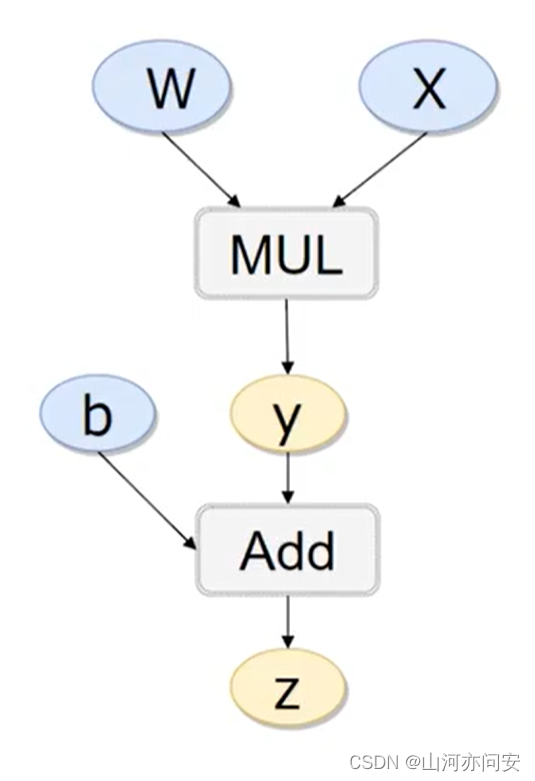
import torch

x=torch.tensor(1.,requires_grad=True)
b=torch.tensor(2.,requires_grad=True)
w=torch.tensor(3.,requires_grad=True)
z=w*x+b
z.backward()#反向传播
print(x.grad)#x导数值
print(w.grad)#w导数值
print(b.grad)#b导数值

运行结果如下图：

要想使上面的x,b,w支持求导，必须让它们为浮点类型，也就是我们给初始值的时候要加个点：“.”。不然的话，就会报错。

1.1.2 二阶导数

import torch

x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()
z = x * x * y
z.backward(create_graph=True) # x.grad = 12
print(x.grad)
x.grad.data.zero_() #PyTorch使用backward()时默认会累加梯度，需要手动把前一次的梯度清零
x.grad.backward() #对x一次求导后为2xy，然后再次反向传播
print(x.grad)

运行结果如下图：

1.1.3 向量

在pytorch里面，默认：只能是【标量】对【标量】，或者【标量】对向【量/矩阵】求导

在深度学习中在求导的时候是对损失函数求导，损失函数一般都是一个标量，参数又往往是向量或者是矩阵。

比如有一个输入层为3节点的输入层，输出层为一个节点的输出层，这样一个简单的神经网络，针对一组样本而言，有

X=（x1,x2,x3）=(1.5,2.5,3.5)，X是（1,3）维的，输出层的权值矩阵为W=（w1,w2,w3）W=(0.2,0.4,0.6)T，这里表示初始化的权值矩阵，T表示转置，则W表示的是（3,1）维度，偏置项为b=0.1,是一个标量，则可以构建一个模型如下：

Y=XW+b，其中W，b就是要求倒数的变量，这里Y是一个标量，W是向量，b是标量，W，b是叶节点。

将上面展开得到：

Y=x1*w1+x2*w2*x3*w3+b

import torch

# 创建一个多元函数，即Y=XW+b=Y=x1*w1+x2*w2*x3*w3+b，x不可求导，W,b设置可求导
X = torch.tensor([1.5, 2.5, 3.5], requires_grad=False)
W = torch.tensor([0.2, 0.4, 0.6], requires_grad=True)
b = torch.tensor(0.1, requires_grad=True)
Y = torch.add(torch.dot(X, W), b)


# 求导，通过backward函数来实现
Y.backward()

# 查看导数，也即所谓的梯度
print(W.grad)
print(b.grad)

运行截图如下：

1.2 线性回归实战

定义一个y=2*x+1线性方程，下面是一个使用 PyTorch 实现线性回归模型，并利用自动求导训练模型的示例：


import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim

x_values=[i for i in range(11)]
x_train=np.array(x_values,dtype=np.float32)
x_train=x_train.reshape(-1,1)


y_values=[2*i +1 for i in x_values]
y_values=np.array(y_values,dtype=np.float32)
y_train=y_values.reshape(-1,1)


#这里线性回归就相当于不加激活函数的全连接层
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)

    def forward(self, x):
        return self.linear(x)



#使用GPU训练
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# 创建模型实例和优化器
model = LinearRegression()
model.to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 定义损失函数
criterion = nn.MSELoss()
for epoch in range(100):
    # 创建数据集
    inputs = torch.from_numpy(x_train).to(device)
    targets = torch.from_numpy(y_train).to(device)
    # 前向传播
    outputs = model(inputs)
    loss = criterion(outputs, targets)

    # 反向传播和优化器更新
    #梯度清零每一次迭代
    optimizer.zero_grad()
    #反向传播
    loss.backward()
    #更新权重参数
    optimizer.step()
    #每10轮，打印一下损失函数
    if epoch%10==0:
        print("epoch {}, loss {}".format(epoch,loss.item()))


#使用训练完的模型进行数据的预测
predicted=model(torch.from_numpy(x_train).to(device))
print(predicted)
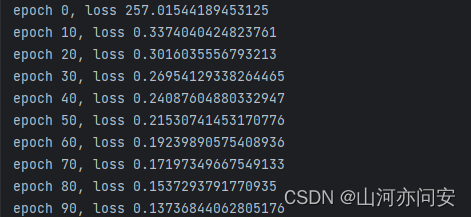
print(targets)

在上面的例子中，我们首先创建了一个简单的线性回归模型 LinearRegression，并创建了一个包含11个样本的数据集。然后，我们定义了损失函数 criterion 和优化器 optimizer，并在训练循环中进行模型训练。

模型训练中损失值变化如下：