问题描述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例1

输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

示例2

输入：digits = “”
输出：[]

示例 3

输入：digits = “2”
输出：[“a”,“b”,“c”]

提示

• 0 <= digits.length <= 4
• digits[i] 是范围 [‘2’, ‘9’] 的一个数字。

思路分析

这个问题可以使用回溯法来解决。回溯法是一种通过遍历所有可能的解空间来解决问题的方法。在本问题中，我们需要生成给定数字能表示的所有字母组合，因此可以使用回溯法来生成这些组合。
思路如下:

1. 创建一个字典 digitMap，将每个数字与对应的字母列表进行映射。例如，数字 '2' 对应的字母列表为 ['a', 'b', 'c']。
2. 定义一个递归函数 generateCombos，该函数接收两个参数：当前数字索引 index 和部分结果字符串 combo。
3. 在 generateCombos 函数中，首先判断当前数字索引是否超出了字符串的长度。如果超出了，则将部分结果添加到最终结果列表中，并返回。
4. 获取当前数字对应的字母列表，并遍历字母列表。对于每个字母，将其添加到部分结果字符串中，并递归调用 generateCombos 函数，同时将当前数字索引加1。
5. 在回溯过程中，记得要将添加的字母从部分结果字符串中移除，以确保下一次遍历开始时是一个干净的状态。
6. 如果输入的字符串为空，则直接返回空列表。

这个问题的时间复杂度是 O(3^N * 4^M)，其中 N 是输入字符串中对应 3 个字母的数字的个数（如 ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘8’），M 是输入字符串中对应 4 个字母的数字的个数（如 ‘7’, ‘9’）。空间复杂度是 O(N+M)。

代码分析

代码中的回溯法实现主要由两部分组成：letterCombinations 函数和 generateCombos 递归函数。

在 letterCombinations 函数中，我们首先创建了一个 digitMap 字典，用于存储数字与字母列表的映射关系。然后，我们定义了 generateCombos 递归函数，该函数负责生成所有可能的字母组合。

在 generateCombos 递归函数中，我们首先判断当前数字索引是否超出了字符串长度，如果是，则将部分结果添加到最终结果列表中，并返回。这里的递归终止条件即为当前数字索引等于字符串长度。

接下来，我们获取当前数字对应的字母列表，并遍历字母列表。对于每个字母，我们将其添加到部分结果字符串中，并递归调用 generateCombos 函数，同时将当前数字索引加1。这样，通过不断地添加字母并递归调用函数，直到达到递归终止条件,就可以生成所有可能的字母组合。

需要注意的是，在每次递归调用结束后，我们要将添加的字母从部分结果字符串中移除，以确保下一次遍历开始时是一个干净的状态，这个过程就是回溯的关键所在。

最后，在 letterCombinations 函数中，我们判断输入的字符串是否为空，如果不为空，就调用 generateCombos 函数来生成所有可能的字母组合。最终，我们返回结果列表。

由于题目中规定输入只包含数字 ‘2’ 到 ‘9’，因此我们事先创建了一个 digitMap 字典来存储数字与字母列表的映射关系。这样做的好处是可以减少重复计算，提高代码的执行效率。

通过回溯法，我们可以生成所有可能的字母组合，解决了给定数字能表示的所有字母组合的问题。

完整代码

class Solution(object):
    def letterCombinations(self, digits):
        # 创建数字与字母列表的映射关系
        digitMap = {
            '2': ['a', 'b', 'c'],
            '3': ['d', 'e', 'f'],
            '4': ['g', 'h', 'i'],
            '5': ['j', 'k', 'l'],
            '6': ['m', 'n', 'o'],
            '7': ['p', 'q', 'r', 's'],
            '8': ['t', 'u', 'v'],
            '9': ['w', 'x', 'y', 'z']
        }
        
        # 定义递归函数生成所有可能的字母组合
        def generateCombos(index, combo):
            if index == len(digits):  # 当前数字索引超出字符串长度，递归结束条件
                result.append(combo)  # 将部分结果添加到最终结果列表中
                return
            
            letters = digitMap[digits[index]]  # 获取当前数字对应的字母列表
            for letter in letters:
                generateCombos(index + 1, combo + letter)  # 递归调用，拼接字母并更新数字索引
        
        result = []  # 存储最终结果的列表
        if digits:
            generateCombos(0, '')  # 如果输入字符串不为空，则从索引 0 开始生成字母组合
        
        return result  # 返回最终结果列表

详细分析

首先是定义一个 Solution 类：

class Solution(object):

这段代码定义了一个名为 Solution 的类。

接下来是 letterCombinations 方法的实现：

    def letterCombinations(self, digits):
        digitMap = {
            '2': ['a', 'b', 'c'],
            '3': ['d', 'e', 'f'],
            '4': ['g', 'h', 'i'],
            '5': ['j', 'k', 'l'],
            '6': ['m', 'n', 'o'],
            '7': ['p', 'q', 'r', 's'],
            '8': ['t', 'u', 'v'],
            '9': ['w', 'x', 'y', 'z']
        }

在 letterCombinations 方法中，我们首先创建了一个名为 digitMap 的字典，用于存储数字与字母列表的映射关系。

接下来定义了内部函数 generateCombos：

        def generateCombos(index, combo):
            if index == len(digits):
                result.append(combo)
                return
            
            letters = digitMap[digits[index]]
            for letter in letters:
                generateCombos(index + 1, combo + letter)

在 generateCombos 方法中，首先判断当前数字索引是否等于字符串长度，如果相等，说明已经遍历完了所有数字，将组合结果 combo 添加到结果列表 result 中，并返回。

根据当前数字索引从 digitMap 中获取对应的字母列表，存储在变量 letters 中。

通过一个循环遍历 letters 中的每个字母 letter，并递归调用 generateCombos 方法，传入下一个数字的索引 index + 1 和新的组合结果 combo + letter。

在 letterCombinations 方法中继续实现：

        result = []
        if digits:
            generateCombos(0, '')
        
        return result

这段代码首先创建了一个空列表 result，用于存储最终的组合结果。

然后，判断输入的 digits 字符串是否为空。如果不为空，说明有输入数字，就调用内部函数 generateCombos，传入初始数字索引为0和空字符串 ''，开始递归地生成所有可能的字母组合。

最后，返回最终的组合结果列表 result。

运行效果截图

调用示例

solution = Solution()
digits1 = "23"
digits2 = ""
digits3 = "2"
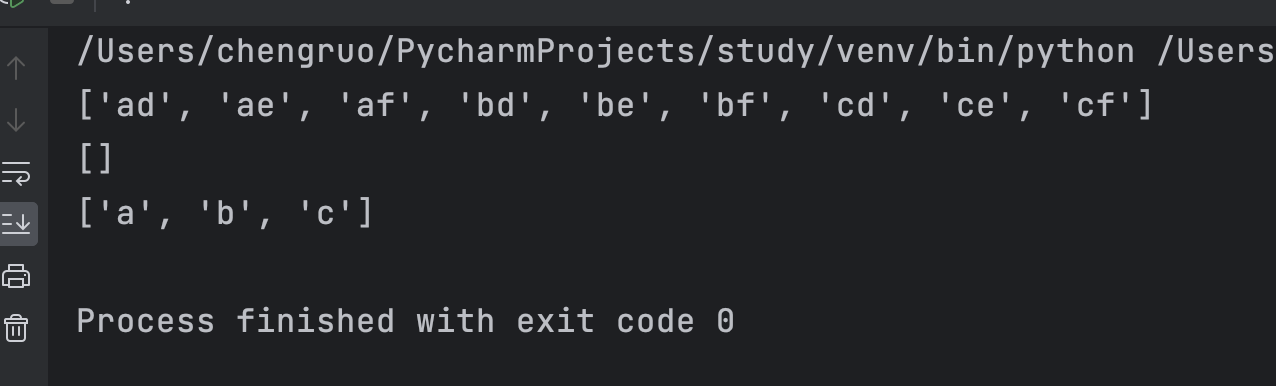
print(solution.letterCombinations(digits1))
print(solution.letterCombinations(digits2))
print(solution.letterCombinations(digits3))

运行结果

完结