2020年国赛高教杯数学建模
D题 接触式轮廓仪的自动标注
原题再现
轮廓仪是一种两坐标测量仪器(见图1),它由工作平台、夹具、被测工件、探针、传感器和伺服驱动等部件组成(见图2)。
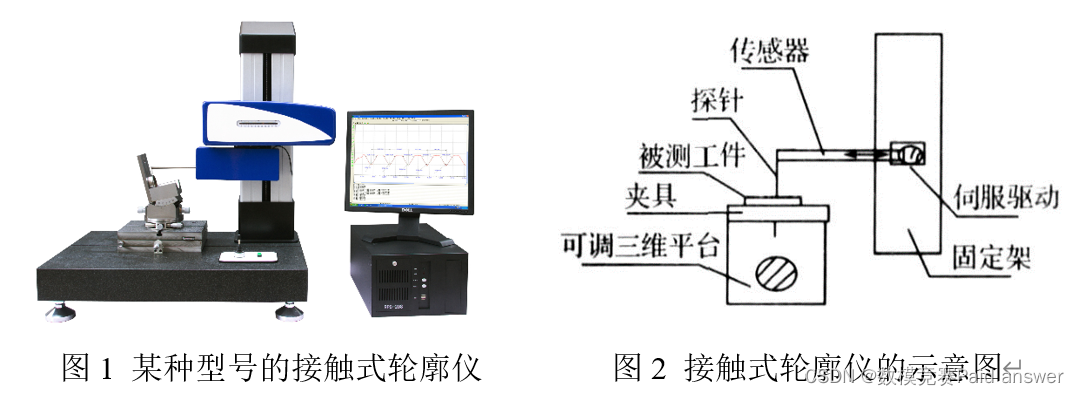
接触式轮廓仪的工作原理是,探针接触到被测工件表面并匀速滑行,传感器感受到被测表面的几何变化,在X和Z方向分别采样,并转换成电信号。该电信号经放大等处理,转换成数字信号储存在数据文件中(见图3)。
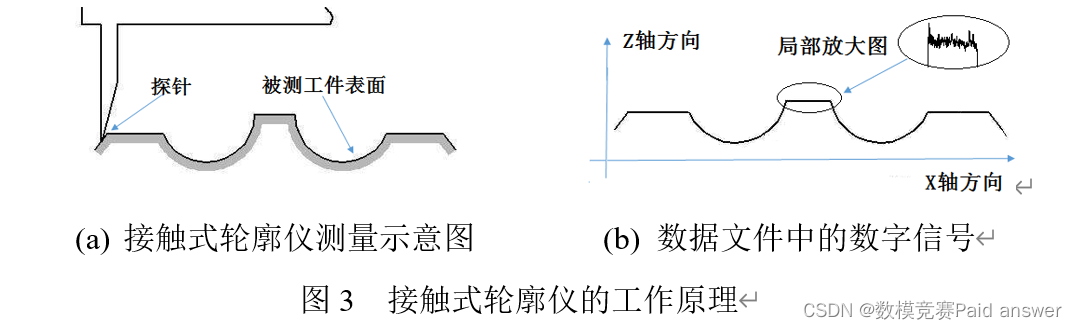
在理想状况下,轮廓曲线应该是光滑的,但由于接触式轮廓仪存在探针沾污、探针缺陷、扫描位置不准等问题,检测到的轮廓曲线呈现出粗糙不平的情况(见图3(b)中的局部放大图),这给工件形状的准确标注带来影响。
为了简化问题,假设被测工件的轮廓线是由直线和圆弧构成的平面曲线(见图4)。请建立数学模型,并根据附件1(工件1的水平和倾斜测量数据)、附件2~附件4(工件2的多次测量数据)所提供的轮廓仪测量数据,研究下列问题:
问题1.附件1中的表level是工件1在水平状态下的测量数据,其轮廓线如图4所示,请标注出轮廓线的各项参数值:槽口宽度(如x_1,x_3等)、圆弧半径(如R_1,R_2等)、圆心之间的距离(如c_1,c_2等)、圆弧的长度、水平线段的长度(如x_2,x_4等)、斜线线段的长度、斜线与水平线之间的夹角(如∠1,∠2等)和人字形线的高度(z_1)。
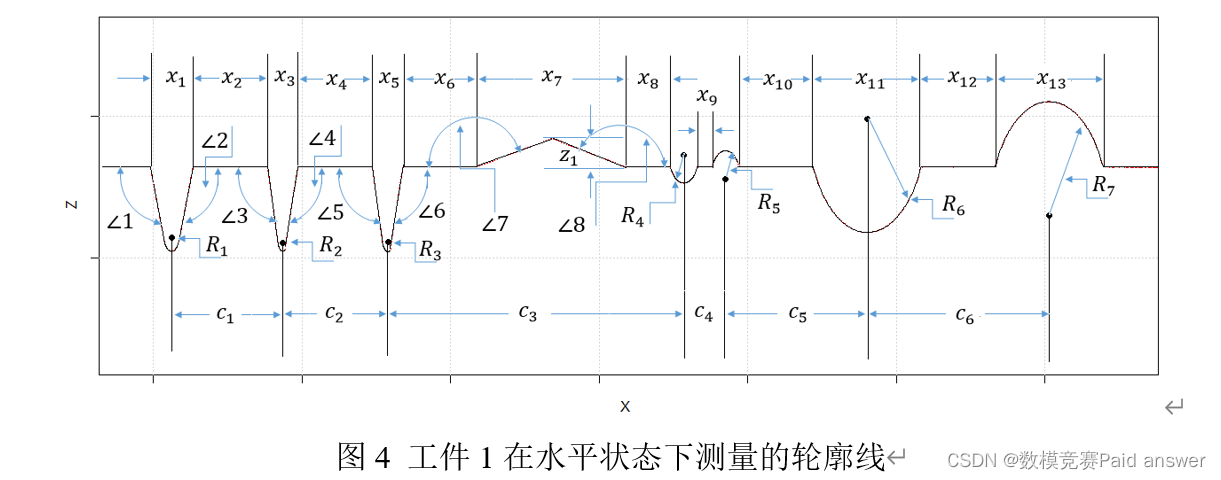
问题2.同一工件在不同次测量时,由于工件放置的角度和位置不同,轮廓线参数的计算值也会存在差异。附件1中的表down给出了工件1在倾斜一个角度和有一些水平位移状态下轮廓线的测量数据。请计算该工件测量时的倾斜角度,并作水平校正。在数据校正后,完成问题1的任务,并比较两种测量状态下工件1各项参数计算值之间的差异。
问题3.在对工件作多次检测时,工件每次放置的角度、测量的起点和终点都会有偏差,这导致了每次测量实际是对整个工件中的某一部分进行检测。附件2提供了对工件2的10次测量数据,请基于这些数据完成:(1) 每次测量时工件2的倾斜角度;(2) 标注出工件2轮廓线的各项参数值(同问题1);(3) 画出工件2的完整轮廓线。
问题4.为了更准确地标注出工件2的各项参数值,附件3和附件4分别提供了工件2关于圆和角的9次局部测量数据,请利用这些数据修正问题3的结论,并对该工件的完整轮廓线作进一步修正。
整体求解过程概述(摘要)
接触式轮廓仪在测量工件或产品的轮廓时,由于存在探针沾污、扫描位置不准等问题,会对工件形状的准确标注带来影响,本文基于接触式轮廓仪的测量数据,研究工件形状的自动标志方法。
针对问题一,本文首先采用一种基于一阶二阶导数的模式识别方法,以此作为理论基础区分水平线、斜线和圆。针对测试数据中的噪声问题,采用一种基于滑动平均的去噪方法。并比较了有重叠滑动窗口和无重叠滑动窗口的去噪效果。通过以上方法可以确定不同曲线段的形状,然后采用一种基于直线和圆的方程的拟合方法,对不同曲线段数据进行拟合,求得各个分段函数方程。最后计算得出直线夹角、半径等参数。与原始数据图形对比,基本吻合。
针对问题二,本文采用一种基于直线旋转量的图形校正方法。水平平移不改变直线的斜率,工件的倾斜旋转的角度就是直线夹角的旋转量。首先采用问题一的方法识别出直线的图形区域,再计算倾斜后的直线旋转量,并基于此进行图形校正。校正后的数据与问题一原始数据对比误差较小。
针对问题三,本文采用一种基于多组测量数据复原完整轮廓的方法。首先采用问题一方法识别出每组数据不同曲线段的形状。然后基于问题二水平直线的旋转量对各组数据进行校正,最后综合各组数据的公共部分和左右两侧的最大冗余数据进行拼接,复原完整轮廓。
针对问题四,本文采用一种基于多组局部数据修正全局图像的方法。首先采用问题一方法识别出每组局部数据不同曲线段的形状。然后通过拟合计算不同曲线段形状的方程和参数,最后等效替代全局图形中对应部分的方程和参数,实现基于局部数据对全局图形的修正。
模型的评价。以上工件自动标注方法,可以较好的替代人工计算,很大程度的解决了接触式轮廓仪工作中存在的问题,标注误差较小。
模型假设:
1) 假设被测工件的轮廓线是由直线和圆弧构成的平面曲线:
2) 假设接触式轮廓仪检测准确没有误差;
3) 假设工件检测的轮廓线无外界干扰
问题分析:
针对问题一,根据水平放置的工件1的测量数据,计算工件自身轮廓线的参数,已知轮廓线是由直线和圆构成,那么问题的关键是我们用什么指标和区分圆和直线,注意到直线的二阶导数为零,而圆的二阶导数不为零,用二阶导数区分圆和直线,而斜线和水平线可以用一阶导数来区分。利用区分好的数据进行圆和直线的拟合从而得到圆和直线的函数表示,再得到整个轮廓线的分段函数表达,进而可以得到各种参数。
针对问题二,已知倾斜放置工件1的测量数据和水平放置工件1的测量数据计算倾斜角度和水平平移量。首先利用前面第一问的方法区分出来直线和圆,把水平测量和倾斜测量的多个圆的位置做对比,得到多个圆的平移量,取平均得到整体轮廓线的平移量;注意到工件1的水平测量数据中有很多的水平线,倾斜之后变成斜线,计算多条斜线的倾斜角取平均得到工件1的倾斜角度;最后利用倾斜角度和平移量通过矩阵相乘把倾斜放置的工件2的测量数据计算得到水平放置的测量数据,然后利用问题1的计算参数方法计算得到工件1水平校正后轮廓线的参数,最后和工件 1 真实水平测量的标注参数进行对比。
针对问题三,题目中给出对工件2的10次不同的测量数据,首先计算每次测量工件2的倾斜角度,我们假设工件2中本身有很多的水平线,仍然使用问题一的方法区分出直线和圆,那么斜率差不多相等的直线段比较多,然后倾斜角的平均,就为此次测量的倾斜角度;其次,因为多次测量位置不同,每次测量的整个工件2的部分,所以我们把每次的测量数据乘以旋转矩阵水平校正后,通过对比,得到整体工件2水平校正后的数据,然后利用问题 1 的方法标注参数;最后,通过水平校正后的数据画出工件 2 的完整的轮廓线。
针对问题四,附件中给出了 9 次角和圆的9 次局部测量数据,修正工件 2的参数,并给出修正后的完整轮廓线。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
clc,clear;
close all;
%导入数据
gjl=xlsread('附件1_工件 1的测量数据');
x_gjl=gj1(:,1);z_gjl=gj1(:,2);
plot(x_gjl,z_gjl)
%设置窗口大小及存放一阶导数、二阶导数、均值、方差等的数组
size_chuangkou=1000;
p=round(length(x_gj1)/size_chuangkou)-2;
m=ones(p,1);
n=ones(p,1);
x_new=ones(p,1);
z_new=ones(p,1);
zhi_m=ones(p,1);
zhi_n=ones(p,1);
zhi_x_new=ones(p,1);
%求一阶导数 k1、二阶导数 k2 以及根据窗口去噪的方法求窗口均值和方差
for d=l:p
v=(d-1)*size_chuangkou;
kl=ones(size_chuangkou);
for i=1:size_chuangkou
k1(i)=(z_gjl(i+v+1)-z_gjl(i+v))/(x_gjl(i+v+1)-x_gjl(i+v));
end
k2=ones(size_chuangkou);
for i=1:size_chuangkou
k2(i)=(k1(i+1)-k1(i))/(x_gjl(i+v+1)-x_gj1(i+v));
end
m(d)=mean(k2(1:size_chuangkou));
n(d)=var(k2(1:size_chuangkou));
x_new(d)=x_gjl(d*size_chuangkou+1);
z_new(d)=z_gjl(d*size_chuangkou+1);
zhi_m(d)=mean(k1(1:size_chuangkou));
zhi_n(d)=var(kl(l:size_chuangkou));
zhi_x_new(d)=x_gjl(d*size_chuangkou+1);
end
%plot(zhi_x_new(1:p),zhi_m(l:p),'.')
%hold on
%设置二阶导数的窗口均值的闯值,抓取圆域所在的位置
x_circle=ones(p,1);
for i=1:p
if m(i)>3.5
x_circle(i)=x_new(i);
end
end
%plot(x_new(l:p),x_circle(l:p),'.')
%hold on
%通过抓取到的圆域的位置,抓取圆域的原始数据以备拟合圆的方程之用
j=0;
x_nihe=ones(20000,1);
z_nihe=ones(20000,1);
for i=1:p
if x_circle(i)>2
for k=1:size_chuangkou
x_nihe(j+k)=x_gjl(i*size_chuangkou+k);
z_nihe(j+k)=z_gjl(i*size_chuangkou+k);
end
j=j+size_chuangkou;
end
end
%圆的拟合计算圆心,半径
%xx=xlsread('新建 Microsoft Excel 工作表');
x=x_gj1(10001:13000) ;y=z_gjl(10001:13000);
N=length(x);
C=N*sum(x.^2)-sum(x)*sum(x);
D=N*sum(x.*y)-sum(x)*sum(y);
E=N*sum(x.^3)+N*sum(x.*y.^2)-sum(x.^2+y.^2)*sum(x);
G=N*sum(y.^2)-sum(y) *sum(y);
H=N*sum(x.^2.*y)+N*sum(y.^3)-sum(x.^2+y.^2)*sum(y);
a=(H*D-E*G)/(C*G-D^2);
b=(H*C-E*D)/(D^2-G*C);
c=-(sum(x.^2+y.^2)+a*sum(x)+b*sum(y)) /N;
A=a/(-2);
B=b/(-2);
R=1/2*sqrt(a^2+b^2-4*c);
%设置一阶导数窗口均值的闯值,抓取直线所在的位置
x_zhi=ones(p);
for i=1:p
if zhi_m(i)>0.15
x_zhi(i)=zhi_x_new(i);
end
if x_circle(i)>2
x_zhi(i)=1;
end
end
plot(zhi_x_new(1:p),x_zhi(1:p),'.')
hold on
title('level 水平直线位置 (窗口: 1000; )')
%通过抓取到的直线的位置,抓取直线的原始数据以备拟合直线的方程之用
s=0;
x_nihe_zhi=ones(20000,1);
z_nihe_zhi=ones(20000,1);
for i=1:p
if x_zhi(i)>2
for k=1:size_chuangkou
x_nihe_zhi(s+k)=x_gjl(i*size_chuangkou+k);
z_nihe_zhi(s+k)=z_gj1(i*size_chuangkou+k);
end
s=s+size_chuangkou;
end
end
%直线的拟合求出斜率和截距
x=x_gj1(22301:23500)';y=z_gj1(22301:23500)';
%x=x_nihe_zhi(17101:19700)';y=z_nihe_zhi(17101:19700)';
a = X*X';
b = sum(x);
c=x*y';
d = sum(y);
N=length(x);
%求解斜率k
k = (N.*c-b*d)./(N.*a-b*b);
%求解截距 t
t = (a.*d-c.*b)/(a*N-b.*b)
plot(x, y,'+')
hold on
plot(x,k*x+t,'.')
title('level 第二条递减直线(从左边看)')
legend('实际','拟合')
%图形的旋转矫正和水平偏移矫正
xuanZhuanJiao=0.130361871364958;
x_jiaoZheng=cos(xuanZhuanJiao)*x_gjl_down-sin(xuanZhuanJiao)*z_gjl_down ;
z_jiaoZheng=sin(xuanZhuanJiao)*x_gjl_down+cos(xuanZhuanJiao)*z_gjl_down ;
z_weitiao=mean(z_jiaoZheng)-mean(z_gjl_level);
x_weitiao=mean(x_jiaoZheng)-mean(x_gjl_level);
x_pianyi=x_weitiao+0.33;
z_jiaoZheng_chuizhi=z_jiaoZheng-z_weitiao;
x_jiaoZheng_shuiping=x_jiaoZheng-x_pianyi;
plot(x_gjl_level,z_gjl_level)
hold on
plot(x_jiaoZheng_shuiping,z_jiaoZheng_chuizhi)
title('level 图与进一步水平矫正后 down 图的比较')
legend('level','down 水平矫正后')
%问题中参数的计算
y0=mean(z_gj1(14690:21690));
kd1=-2.723867741639066; bd1=133.8002234310488;
kd2=-3.724845609376202; bd2=213.0069757236736;
kd3=-3.723602901285295; bd3=239.2514907860618;
kd4=-0.200744158613707; bd4=14.645116449010247;
kd5=-0.565025739534814; bd5=45.935780974909875;
kd6=-1.123311555044076; bd6=98.725881910432650;
kd7=-0.343117911107307; bd7=29.331114981311476;
kd8=-0.425604356360074; bd8=47.817846154298124;
ku1=2.754359108225884; bu1=-146.8171658730294;
ku2=2.980598439534949; bu2=-179.8507093519987;
ku3=3.511651703755757; bu3=-236.2555247229892;
ku4=0.194764774178566; bu4=-15.745625965295059;
ku5=1.312714609538673; bu5=-115.4903009149167;
ku6=1.119240436916190; bu6=-99.776517012025040;
ku7=1.472580398274092; bu7=-151.5742987893202;
ku8=1.001404926554808; bu8=-108.2696306825218;
k2u1=1.873469412912976; b2u1=-102.8003499165892;
k2u2=2.441766357967081; b2u2=-152.1327739769671;
k2u3=2.414152499053679; b2u3=-168.2737582070639;
k2d1=-0.129926436840446; b2d1=7.740846276449202;
k2d2=-0.130937034696584; b2d2=7.799039243107876;
k2d3=-0.131141148034880; b2d3=7.813060406404597;
k2d4=-0.131105391993604; b2d4=7.811663609602934;
%下降曲线的折现点横坐标
td1=(y0-bd1)/kd1;
td2=(y0-bd2)/kd2;
td3=(y0-bd3)/kd3;
td4=(y0-bd4)/kd4;
td5=(y0-bd5)/kd5;
td6=(y0-bd6)/kd6;
td7=(y0-bd7)/kd7;
td8=(y0-bd8)/kd8;
%上升曲线的折现点横坐标
tu1=(y0-bu1)/ku1;
tu2=(y0-bu2)/ku2;
tu3=(y0-bu3)/ku3;
tu4=(y0-bu4)/ku4;
tu5=(y0-bu5)/ku5;
tu6=(y0-bu6)/ku6;
tu7=(y0-bu7)/ku7;
tu8=(y0-bu8)/ku8;
x1=tu1-td1;
x2=td2-tu1;
x3=tu2-td2;
x4=td3-tu2;
x5=tu3-td3;
x6=tu4-tu3;
x7=td4-tu4;
x8=td5-td4;
x9=tu6-tu5;
x10=td7-td6;
xll=tu7-td6:
x12=tu8-tu7;
x13=td8-tu8;
j1=atan(kd1)*180/3.141592+180;
j2=180-atan(ku1)*180/3.141592;
j3=atan(kd2)*180/3.141592+180;
j4=180-atan(ku2)*180/3.141592;
j5=atan(kd3)*180/3.141592+180;
j6=180-atan(ku3)*180/3.141592;
j7=180-atan(ku4)*180/3.141592;
j8=atan(kd4)*180/3.141592+180;
xuanzhuanjiao1=atan(ku1)*180/3.141592-atan(k2u1)*180/3.141592;
xuanzhuanjiao2=atan(ku2)*180/3.141592-atan(k2u2)*180/3.141592;
xuanzhuanjiao3=atan(ku3)*180/3.141592-atan(k2u3)*180/3.141592;
xuanzhuanjiao4=atan(k2d1)*180/3.141592;
xuanzhuanjiao5=atan(k2d2)*180/3.141592;
xuanzhuanjiao6=atan(k2d3)*180/3.141592;
xuanzhuanjiao7=atan(k2d4);
y_jian=bu4+ku4*(bd4-bu4)/(ku4-kd4)-y0;
x_jian=(bd4-bu4)/(ku4-kd4);

![[Java]重写equals为什么要重写hashcode???配合HashMap源码一起理解](https://img-blog.csdnimg.cn/42c749145e29456a8bdca0a824cb01ea.png)