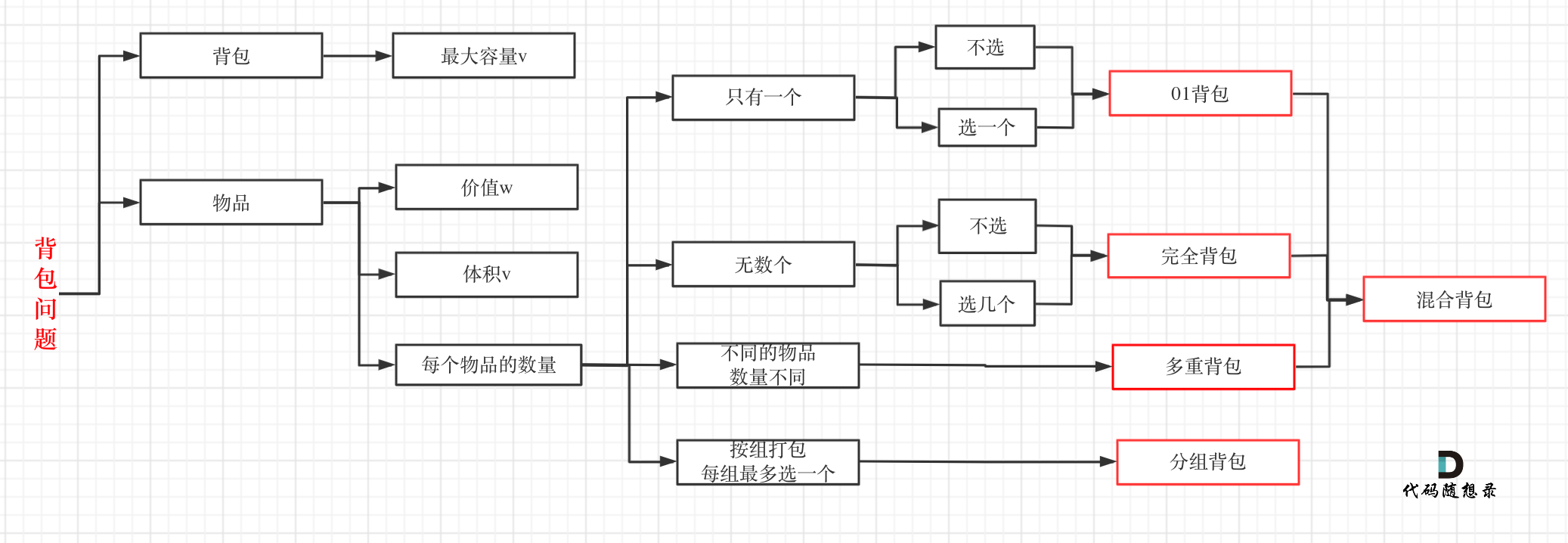
● 01背包问题，你该了解这些！

二维dp数组

● 01背包问题，你该了解这些！ 滚动数组

一维dp数组

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

● 416. 分割等和子集 

本题属于01背包问题的应用，

这道题目是要找是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

那么只要找到集合里能够出现 sum / 2 的子集总和，就算是可以分割成两个相同元素和子集了。

本题是可以用回溯暴力搜索出所有答案的，但最后超时了，

只有确定了如下四点，才能把01背包问题套到本题上来。

• 背包的体积为sum / 2
• 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
• 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素是不可重复放入。

以上分析完，我们就可以套用01背包，来解决这个问题了。

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        //首先将本题转换成01背包问题 
        int sum = 0;
        for(int i = 0;i<nums.size();i++){
            sum += nums[i];
        }
        if(sum % 2 == 1) return false;//如果总和不能对半分，则分出来的两个自己和一定不相等，直接return false
        
        int target = sum / 2;//容量为trget的背包能否装重量target的物品

        vector<int> dp(10001,0);//容量为i的背包最多可以装价值为dp[i]的物品 nums中每个元素值小于100，最多元素为200个，所以总和最多20000，一半的话最多为10000，所以初始化dp的大小为10001，每个值都为0

        for(int i = 0;i<nums.size();i++){//遍历每个物品
            for(int j = target;j>=nums[i];j--){//遍历背包的容量
                dp[j] = max(dp[j],dp[j - nums[i]] + nums[i]);
                if(dp[j] == target){
                    return true;
                }
            }
        }

        return false;


    }
};