💥1 概述

小波哈尔法（WHM）是一种求解一维非线性初值问题（IVP）的数值方法。它基于小波分析的思想，通过将原始问题转化为小波空间中的线性问题，然后进行求解。以下是一维非线性IVP测试问题的求解步骤：

1. 确定目标问题：首先，确定你要解决的一维非线性IVP测试问题。这可能涉及到一个非线性的微分方程和一些边界条件。

2. 小波基函数选择：选择适当的小波基函数来表示问题中的解。小波基函数应该具有良好的局部特性和适应性，以便更好地表示原始问题。常见的小波基函数包括Haar小波、Daubechies小波和Symlet小波等。

3. 建立小波变换：通过将问题转化为小波空间中的线性问题来建立小波变换。这可以通过将解函数和微分方程表示为小波基函数的线性组合来实现。

4. 线性方程求解：将小波变换应用于原始问题后，将其转化为一组线性方程。通过求解这组线性方程来获得小波系数，从而得到原始问题的近似解。

5. 逆小波变换：将得到的小波系数和小波基函数的逆变换应用于小波空间，将解转换回原始空间。这将给出原始问题的近似解。

6. 结果评估：评估求解结果的准确性和收敛性。可以比较近似解与真实解之间的差异，并检查所采用的小波基函数的适用性。

需要注意的是，小波哈尔法（WHM）是一个高级的数值方法，需要掌握小波分析和线性代数的基础知识。在实施过程中，还需进行适当的数值技巧，如数值积分和线性方程求解等。

📚2 运行结果

 

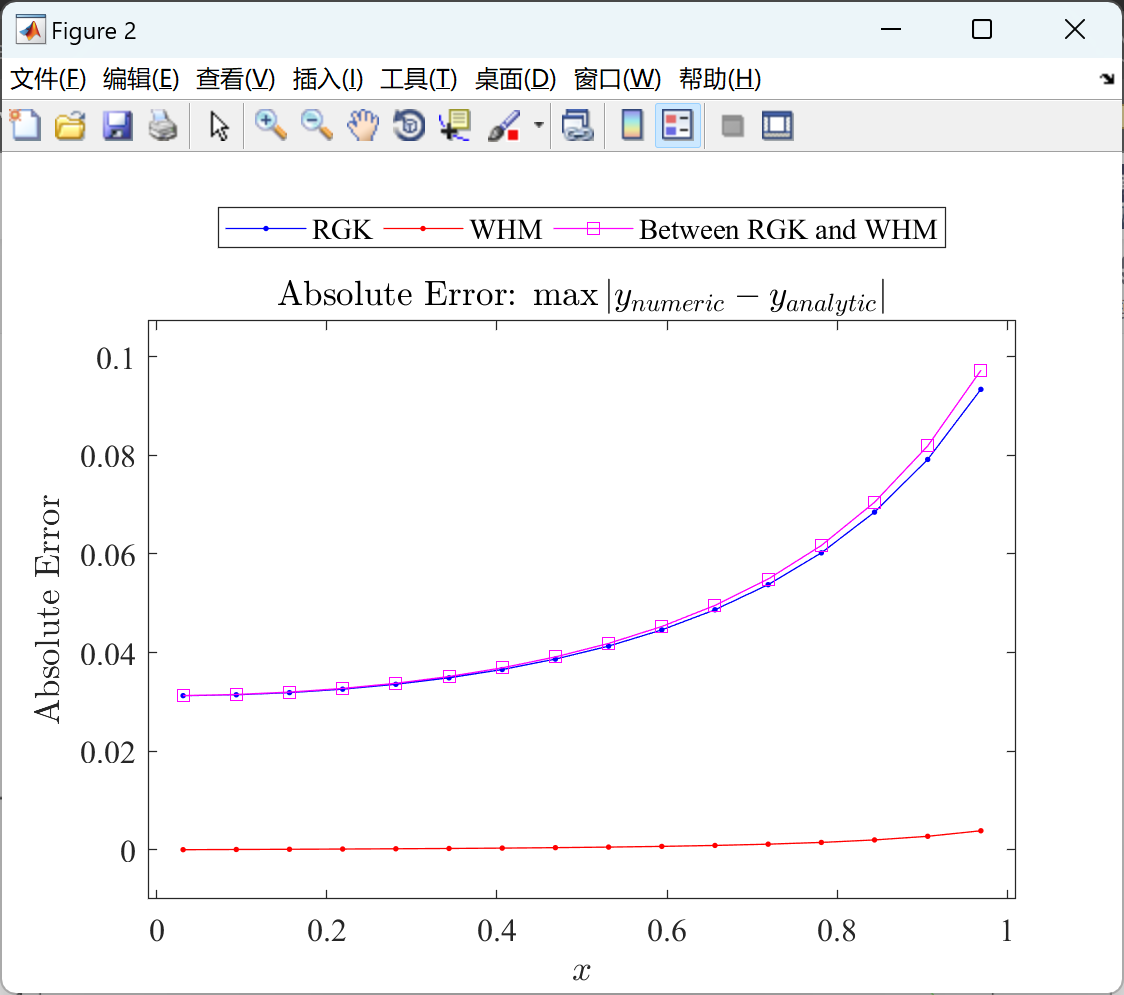
部分代码：

% step 1
% collocation points
J = 3;                              % level of decomposition
N = 2^(J + 1); % N = 2M             % number of basis functions
j = 1:N;                            % index of grid points
x = (j - 0.5) ./ N;                 % grid points

% step 2
% initial values
alpha1 = 0;                         % initial value of a function
beta1  = - 1;                       % initial value of the first derivative
a1     = beta1 - alpha1;

% step 3
% Newton solver
W = zeros(N,N);
f = zeros([N 1]);
a = zeros([N 1]);

epsilon = 1e-4;
r = ones([N 1]);

iter_ind = 0;
tic
while max(r) > epsilon   
    for j = 1:N
        % f(x) computation 
        % H, P1, P2 computation
        H = 0;               
        P1 = 0;
        P2 = 0;
        for i = 1:N
            H  = H  + a(i) * haar(x(j), i, J);
            P1 = P1 + a(i) * p1(x(j), i, J);
            P2 = P2 + a(i) * p2(x(j), i, J);            
        end;
        
        f(j) = 2 * (alpha1 + beta1 * x(j) + P2) * ...
            (beta1 + P1) + H;  
        
        
        % W(x) matrix computation        
        for k = 1:N
            W(j,k) = 2 * p2(x(j),k,J) * (beta1 + P1) + ...
                2 * (alpha1 + beta1 * x(j) + P2) * p1(x(j),k,J) + haar(x(j),k,J);            
        end; % for k
    end; % for j
    
    a_new = W \ (W*a - f);      % linear system solution
    r = abs(a_new - a);         % residual 
    disp(['iteration: ' num2str(iter_ind) ' error Newton: ' num2str(max(r))])   
    
    % Update variables
    a = a_new;
    iter_ind = iter_ind + 1;
end; % while
toc

% Reconstruct approximate solution
y = zeros(N,1);
for j = 1:N    
    S = 0;
    for i = 1:N
        S = S + a(i) * p2(x(j),i,J);
    end
    y(j) = alpha1 + x(j) * beta1 + S;
end; % for

%% Exact solution
yexact = - tan(x);
% critical point pi/2 ~= 1.5708
x_zero1 = 0.5 * pi; 

%% Runge - Kutta method
[x, y1] = ode113('model0', x, [alpha1 beta1]);

%% Plot graphics
set(0,'defaulttextinterpreter','latex')
set(0,'defaultaxesfontname','times')
set(0,'defaultaxesfontsize',12)

oft = 0.01;

% fig:01
figure('color','w')
plot(x,yexact,'g',x,y,'rs',x,y1(:,1),'b.')
xlabel('$x$'); ylabel('$y$');
title(['J = ' num2str(J) ', ' '2M = ' num2str(N)])
legend('Exact','WHM', 'RGK')
axis([-oft 1+oft min(yexact)-oft max(yexact)+oft])

% Absolute errors
rRGK = abs(y1(:,1) - yexact');
rWHM = abs(y - yexact');
rRW = abs(y - y1(:,1));

% fig:02
figure('color','w')
plot(x,rRGK,'b.-',x,rWHM,'r.-',x,rRW,'ms-')
xlabel('$x$'); ylabel('Absolute Error');
title('Absolute Error: $\max|y_{numeric} - y_{analytic}|$')
legend('RGK','WHM','Between RGK and WHM',...
    'Location','northoutside','Orientation','horizontal')
axis([-oft 1+oft min([rRGK; rWHM; rRW])-oft max([rRGK; rWHM; rRW])+oft])

%% Disp Errors
disp(['error RGK: ' num2str(max(rRGK)) ' error WHM: ' num2str(max(rWHM)) ...
    ' error RW: ' num2str(max(rRW))])

%% Save data
if flag == 1    
    cd 'dat'
    
    table0 = [x yexact' y y1(:,1)];
    fid = fopen('table0.txt','w');
    fprintf(fid, '%6.2f %6.2f %6.2f %6.2f\n', table0');
    
    fclose(fid);
    disp('Saved.')
 

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1] Siraj-ul-Islam, Imran Aziz, Bozidar Sarler, "The numerical solution 
      of second-order boundary-value problems by collocation method with 
      the Haar wavelets,"Mathematical and Computer Modelling, Vol. 52, 
      No. 9-10, 1577-1590, 2012.

[2] Sahoo, Bishnupriya, "A study on solution of differential equations 
      using Haar wavelet collocation method, MSc thesis, 2012.
 

🌈4 Matlab代码实现