[ 数据结构 ] 排序算法--------七大内排,看完还不会写来揍我

news2025/2/24 9:26:52

0 前言

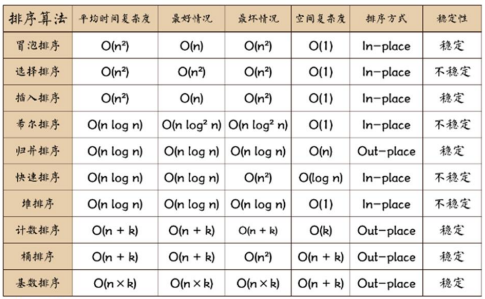
1.1 排序分类

  • 内部排序和外部排序,前者数据加载到内存,后者数据量大需借助外部文件.

  • 内部排序包含:

    插入排序:直接插入排序,希尔排序

    选择排序:简单选择排序,堆排序

    交换排序:冒泡排序,快速排序

    归并排序

    基数排序

1.2 复杂度

1)度量一个程序时间有两种方法,事后统计或事前估算,事前估算就需要分析时间复杂度

2)时间复杂度:算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数,

​ 计算方法:去常数阶–>保留最高阶项–>去除最高阶项系数

​ 常见时间复杂度:常数阶 O(1)、对数阶 O(log2n)、线性阶 O(n)、线性对数阶 O(nlog2n)、平方阶 O(n^2)、立方阶 O(n^3)、k 次方阶 O(n^k)、指数阶 O(2^n)

​ 对应结构:普通无循环结构语句、while循环、for循环、外层for内部while结构、2层for循环…

3)空间复杂度:度量程序占用的存储空间大小,比如基数排序的空间换时间

1 冒泡排序

思路:

  1. 说明:本文以从小到大排序作为顺序排序进行举例说明,print(int[] arr)为打印方法,使用面向过程编程,没有面向对象和封装操作
  2. 代码核心:两层for循环+交换
  3. 微观理解:外层for:表示进行第几轮排序,内层for:比较相邻元素并将较大值交换到右边
  4. 宏观理解:每一轮的作用可以简单认为将最大值放在最右边,数组有n个元素,因此需要求n-1次最大值,即需要arr.length-1轮
  5. 对比说明:这里的交换法需要区别插入排序和希尔排序中的交换法,这里的交换法使用的目的是将一个无序数组的最大值通过两两交换最终弄到最右边,原来的无序数组仍然很可能是无序的,而希尔/插入中交换法的目的是将一个任意值从有序数组的最右边,通过交换的手段插入到正确位置,原来的有序数组仍然一定是有序的

优化:

​ 如果本轮没有进入交换操作的代码,说明数组已经有序,退出循环

private static void sort(int[] arr) {
        int temp;
        boolean flag = true;
        for (int i = 0; i < arr.length - 1; i++) {//每完成一轮排序则排除一个最大值,剩余的是无序数组,注意区别插入排序中的交换法
            for (int j = 0; j < arr.length-i-1; j++) {
                if (arr[j] > arr[j + 1]) {
                    flag = false;
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
            System.out.println("完成第"+(i+1)+"轮排序");
            print(arr);
            //优化:如果本轮没有换位则无需再排
            if (flag) {
                break;
            } else {
                flag = true;
            }

        }
    }

2 选择排序

思路:

  1. 代码核心:两层for循环
  2. 微观理解:外层for:表示进行第几轮排序,内层for:辅助变量收集最小值赋给第一个元素
  3. 宏观理解:每一轮的作用可以简单认为将最小值放在最左边,数组有n个元素,因此需要求n-1次最大值,即需要arr.length-1轮
  4. 对比说明:冒泡排序是比较相邻元素并交换,选择排序是与极值比较且一轮仅交换一次

优化:

​ 如果本轮的第一个元素就是最小值,则不用操作

private static void sort(int[] arr) {

        int min = 0;
        int cor=0;

        for (int j = 0; j < arr.length - 1; j++) {
            //每一轮都默认乱序数组第一个数为该轮最小值
            min = arr[j];
            cor=j;
            for (int i = j; i < arr.length; i++) {
                if (arr[i] < min) {
                    //找到更小的则更新最小值和角标
                    cor = i;
                    min = arr[i];
                }
            }
            //最小值已保存,将第一个数与最小处赋值
            if (cor!=j)//优化:第一个数为最小则无需赋值
                arr[cor] = arr[j];
            arr[j] = min;
            print(arr);
        }

    }

3 插入排序

(移位法)思路:

  1. 代码核心:外层for循环+内层while循环
  2. 微观理解:外层for表示需要几轮插入操作,内部:将待插入数取出,开始从后往前遍历(while循环)有序数组,指针指向待插入数的前一个,只要索引不越界同时待插入数比指针所在数小,就将该数(指针所在)后移并继续前移指针,一旦不满足(待插入数大于指针数)说明插入位置找到,插入则本轮结束
  3. 宏观理解:每一轮的作用就是在左侧的有序数组中插入一个数到正确位置,因为有序数组长度从1到arr.length,所以需要arr.length-1轮

(交换法)思路:

  1. 代码核心:两层for循环
  2. 微观理解:外层for表示需要几轮插入操作,内部:在有序数组的后面多取一个数(待插入数),从后往前遍历(for循环)有序数组,如果发现逆序则执行交换
  3. 宏观理解:每一轮的作用就是在左侧的有序数组中插入一个数到正确位置,因为有序数组长度从1到arr.length,所以需要arr.length-1轮
  4. 交换法对比移位法:移位法用的while循环,原理是没找到就后移,一旦找到就退出循环并插入,交换法用的是for循环,没找到位置就一直交换,一旦不再交换了就说明本轮数组已经有序了
  5. 效率比较:交换法因为需要使用中间变量实现待插入数+遍历数+中间变量间相互赋值而且遍历不会终止,而移位法只需移位(赋值)且一旦找到正确位置遍历当即终止,所以移位法效率更高
private static void sort(int[] arr) {
        //变量声明在循环外更好
        int insertVal =0;
        int insertIndex= 0;
        for (int i = 1; i < arr.length; i++) {
            insertVal = arr[i];//取出待插入数,保证该位置可被后推覆盖
            insertIndex= i-1;//有序数组下界
            //索引不越界下,逆序遍历有序数组,只要待插入值比遍历值小(小到大排序)就将遍历值后推
            while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
                arr[insertIndex + 1] = arr[insertIndex];
                insertIndex--;
            }
            //位置找到,则先补上遍历附带的索引自减1,再将待插入值放入有序数组
            //赋值优化:只有待插入数和有序数组之间已经有序则无需赋值,既然有序则没有上面的后推和遍历,
            //          即索引自减没执行过,因此
            if (insertIndex + 1 != i) {
                arr[insertIndex+1] = insertVal;
                System.out.print("该轮赋值了");
            }
            System.out.print("第"+i+"轮: ");
            print(arr);
        }

    }
    
    
    //等价于sort方法,只是for代替while循环,交换代替了插入的后推及赋值
    //后续的希尔排序就是基于这两种方法的优化
    private static void sort2(int[] arr) {
        int temp = 0;
        for (int i = 0; i < arr.length-1; i++) {
            for (int j = i; j >= 0; j--) {
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = temp;
                }
            }
        }
        print(arr);

    }

4 希尔排序

思路:

  1. 插入排序问题:如果待插入数最小,则后移次数明显增多,arr = {2,3,4,5,6,1},当将1插入时需要后移5次
  2. 希尔排序:基于简单插入排序,加入了分组和步长(增量)的概念,不断缩小组内增量
  3. 简单来讲,就是将数据分组后实现组内排序,步长不断缩小表示组内元素不断增加,数据整体越逆序效果越明显
  4. 简单插入排序就是步长为一所有数据都在一组的希尔排序,也就是希尔的最后一波排序
  5. 代码理解:就是在插入排序的最外层套上for循环,以不断缩小增量直到步长为1

image-20221208233941441.png

//参考插入排序的交换式,加入分组和步长的概念,不断缩小组内增量
    private static void sort1(int[] arr) {
        int temp = 0;
        int count = 0;
        for (int gap = arr.length/2; gap >0 ; gap/=2) {
            for (int i = 0; i < arr.length - gap; i++) {//这里使用i++而不是加步长,才能保证每个组内排序
                for (int j = i; j >=0; j-=gap) {
                    if (arr[j] > arr[j + gap]) {
                        temp = arr[j];
                        arr[j] = arr[j + gap];
                        arr[j + gap] = temp;
                    }
                }
            }
            System.out.print("第"+(++count)+"轮");
            print(arr);
        }

    }

    //参考插入排序的移位法,加入分组和步长的概念,不断缩小组内增量
    private static void sort2(int[] arr) {
        int value = 0;
        int key = 0;
        int count = 0;

        for (int gap = arr.length/2; gap >0 ; gap/=2) {

            for (int i = gap; i < arr.length ; i++) {
                value = arr[i];
                key = i - gap;
                while (key >= 0 && value < arr[key]) {
                    arr[key + gap] = arr[key];
                    key-=gap;
                }
                if (key != i - gap) {
                    arr[key + gap] = value;
                }
            }

            System.out.print("第"+(++count)+"轮");
            print(arr);
        }

    }

5 归并排序

思路:

  1. 代码核心:递归,分治策略
  2. 微观理解:
    • 传参:数组arr,low(排序区间下界索引),high(排序区间上界索引)
    • 终止:上下界相交(即只对组内唯一元素排序)
    • 分:将数据从区间正中分为两组
    • 治:三个指针,顺序遍历两个子数组并将较小值顺序赋给辅助数组,最终将辅助数组(有序)的元素同步到待排序数组arr
  3. 宏观理解:先分后治,先递归分组将数组一直分到每组仅有一个元素,此时递归终止且组内有序(一个元素),层层返回(类似回溯),执行分组操作下面的合并操作(辅助数组+2个子数组+3个指针实现归并)

image-20221209183110601.png

//分治方法,分为递归分组,治为该层的归并排序
    private static void sort(int[] arr,int low ,int high) {
        //辅助数组,用于复制归并后的有序数组
        int[] assist = new int[arr.length];

        //安全性校验,表示该组只有一个元素
        if (high <= low) {
            return;
        }

        //分治法中的分,即分组,也是递归调用,上面的健壮判断可以看成递归终止条件
        int mid = low + ((high - low) >> 1);
        sort(arr, low, mid);
        sort(arr,mid+1,high);

        //当分组完毕(递归终止)后,最终的两组内只有一个元素(即有序),才会执行下面代码,即层层排序返回上层,这里为界,上面为分组,下面为(归并)排序
        //个人理解为:在上面的分组操作没有终止前,一直在做分的操作,直到分组完毕才开始治,治完再治上层
        //举例:本层的上下界为0和1,则上面的分组防止直接不做操作返回,而对两个单元素的子数组做如下的归并排序,返回上层

        //使用三个指针,表示两个子数组的起点索引和归并数组的起点索引
        int i = low;
        int p1 = low;
        int p2 = mid + 1;

        //比较子有序数组的起点值,不断复制最小值到辅助数组并后移指针,直到某一子数组复制完毕
        while (p1 <= mid && p2 <= high) {
            if (arr[p1] < arr[p2]) {
                assist[i++] = arr[p1++];
            } else {
                assist[i++] = arr[p2++];
            }
        }

        //将未复制完的子数组弄完
        while (p1 <= mid) {
            assist[i++] = arr[p1++];
        }
        while (p2 <= high) {
            assist[i++] = arr[p2++];
        }

        //将归并后的顺序同步给请求者
        for (int j = low; j <= high; j++) {
            arr[j] = assist[j];
        }
    }

6 快速排序

思路:

  1. 代码核心:递归
  2. 微观理解:
    • 传参:数组arr,low(排序区间下界索引),high(排序区间上界索引)
    • 终止:上下界相交(即只对组内唯一元素排序)
    • 单层逻辑:取下界值arr[low]为基准值,左右指针最初为区间上界和下界+1,即待分组元素的边界外,开始相向移动,遇到对方的元素则做交换操作,直到两指针相交,交换右指针元素和区间上界(基准值),此时单层排序完成只需对左右子组递归排序即可
  3. 宏观理解:不同于归并排序的分治思想,归并操作(排序)是在分组后才完成的,而快速排序的交换操作(排序)是在分组前就完成了

个人理解+优化:

//问题1:理想条件下,基准值两边交换完后,刚好剩一个小的与基准值交换,如果不剩呢
//  退出while前r指针做了自减,所以指向的一定是左子组的数据
//问题2:如果只有一侧数据呢,怎么交换
//  若只有右组数据,则r最终指向上界即自己换自己,若只有左组数据,l和r在下界相交,只需交换一次基准值即可
//问题3:分组结束的状况是怎么样的,也就是最底层和上两层的情况举例
//  最底层区间只有一个元素,上层则2/3个
//问题4:指针遇到与基准值等值的怎么办?
//	正常交换操作即可,交换后等基准值分到哪一组都不影响正确性
//问题5:什么情况下左右指针相遇?
//	左右指针相交,说明交换完毕/只有一侧有数据,需退出,否则持续交换
//	至于最终l==r还是l>r,看谁先找,以及是否能找到,结果复杂不好判断
//问题6:为什么指针相交后,基准值的交换操作用的是右指针r指的元素,而不是左指针?
//	由问题1知r最终指向左子组,即r的元素比基准值小,因此使用r和lo交换
//优化:
//	基准值的交换操作可以加判断条件,比如该组就两个数且有序,即lo==r,则不用交换

image-20221209183326412.png

最终代码:

//问题1:理想条件下,基准值两边交换完后,刚好剩一个小的与基准值交换,如果不剩呢
    //  退出while前r指针做了自减,所以指向的一定是左子组的数据
    //问题2:如果只有一侧数据呢,怎么交换
    //  若只有右组数据,则r最终指向上界即自己换自己,若只有左组数据,l和r在下界相交,只需交换一次基准值即可
    //问题3:分组结束的状况是怎么样的,也就是最底层和上两层的情况举例
    //  最底层区间只有一个元素,上层则2/3个
    //函数功能:对数组的某一区间进行排序
    private static void sort(int[] arr,int lo ,int hi) {

        //安全性校验:保证区间内不止一个元素
        if (lo >= hi) {
            return;
        }

        //分组:将区间元素(按序)分为左右子组,并拿到基准值最终的角标
        //左右指针最初为区间上界和下界+1,即待分组元素的边界外,开始相向移动
        int l = lo;
        int r = hi+1;
        int temp = 0;
        int pivot = arr[lo];//基准值

        while (true) {
            //右指针向左移,遇到左元素(基准值)停下,或遇到区间上界停下
            //说明:如果指针遇到等基准值,则交换后等基准值分到哪一组都不影响正确性
            while (arr[--r] > pivot) {
                if (r == lo) {
                    break;
                }
            }
            while (arr[++l] < pivot) {
                if (l == hi) {
                    break;
                }
            }
            //左右指针相交,说明交换完毕/只有一侧有数据,需退出,否则持续交换
            //至于最终l==r还是l>r,看谁先找,以及是否能找到,结果复杂不好判断
            if (l >= r) {
                break;
            } else {
                temp = arr[l];
                arr[l] = arr[r];
                arr[r] = temp;
            }
        }
        //使用r作为基准值角标是,因为r最终指向左子组元素
        //当然r也可能是lo上界(本身有序没有交换操作),因此可做优化if(lo===r)
        temp = arr[lo];
        arr[lo] = arr[r];
        arr[r] = temp;

        //左右子组排序
        sort(arr, lo, r-1);
        sort(arr, r+1, hi);
    }

7 基数排序

  1. 代码核心:两层for循环
  2. 微观理解:外层for:表示进行第几轮排序(依次针对个位、十位、百位…),内层for:二维数组表示10个桶,将元素依次放入桶中,顺序遍历桶元素依次同步到原数组
  3. 宏观理解:每一轮的作用可以简单认为针对不同位做桶操作,数组中最大元素有n位,因此需要n轮
  4. 总结:桶排序虽然是按个位十位百位依次排序,但是道理就像先比百位,再比十位,最后个位,得到正确顺序,核心在于辅助数组(二维数组即十个桶,一维数组即十个桶的偏移量)的使用,属于空间换时间,还有,基数排序具有稳定性,因为相同值间的前后顺序不会改变,这是因为所有操作都是基于原本的顺序遍历的

image-20221209182932431.png

private static void sort(int[] arr) {

        //准备工作:
        // 1.开辟一个二维数组(10个桶),每个桶大小和arr保持一致
        // 2.计算数组中最大位数
        int[][] buckets = new int[10][arr.length];
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        int rounds = (max + "").length();

        //元素最高n位,就需要进行n轮排序,依次对个位,十位,百位操作
        for (int round = 0,n=1; round < rounds; round++,n*=10) {

            //每一轮需先重置桶偏移量
            int[] bucketOffset = new int[10];

            //遍历数组元素,计算桶编号,放入对应桶中并更新桶偏移量
            for (int i = 0; i < arr.length; i++) {
                int bucketNo = arr[i]/n % 10;
                buckets[bucketNo][bucketOffset[bucketNo]] = arr[i];
                bucketOffset[bucketNo]++;
            }

            //顺序遍历每个桶中元素,并同步到原数组
            int index = 0;
            for (int i = 0; i < 10; i++) {
                if (bucketOffset[i] != 0) {
                    for (int j = 0; j < bucketOffset[i]; j++) {
                        arr[index++] = buckets[i][j];
                    }
                }
            }
            System.out.print("第" + (round+1) + "轮:");
            print(arr);
        }

    }

8 总结对比

image-20221209175757920.png

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/76464.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

tp3.2实现websocket

tp3.2实现websocket

首先从单服务器实现开始 我的系统是centos系统&#xff0c;lnmp搭建的环境&#xff0c;php5.6 1&#xff1a;首先检查环境是否支持 curl -Ss http://www.workerman.net/check.php | php PHP Version > 5.3.3 [OK] Extension pcntl check [OK] Extension posix check [OK] 2.…
阅读更多...
Metal每日分享，均值模糊滤镜效果

Metal每日分享，均值模糊滤镜效果

本案例的目的是理解如何用Metal实现均值模糊效果滤镜&#xff0c;均值模糊原理其实很简单通过多个纹理叠加&#xff0c;每个纹理偏移量设置不同达到一点重影效果来实现模糊; Demo HarbethDemo地址 实操代码 // 均值模糊效果滤镜 let filter C7MeanBlur.init(radius: 0.5)//…
阅读更多...
清除浏览器缓存

清除浏览器缓存

清除浏览器的缓存知识调用前言引入具体操作知识调用 文章中可能用到的知识点前端学习&#xff1a;浏览器缓存方式有哪些&#xff08;http协议 websql indexDB cookie localstorage sessionstorage&#xff09;如何查看Chrome浏览器的页面缓存内容【详细教程】 前言引入 上期文…
阅读更多...
基于汇编的.NET高级调试

基于汇编的.NET高级调试

一：背景 1. 简介 .NET 高级调试要想玩的好，看懂汇编是基本功，但看懂汇编和能写点汇编又完全是两回事，所以有时候看的多，总手痒痒想写一点，在 Windows 平台上搭建汇编环境不是那么容易，大多还是用微软的 MASM + DosBox 搭一个 8086 的环境，这玩意距今快 50 年了。 在…
阅读更多...
Node.js Event Loop 处理的几大周期介绍

Node.js Event Loop 处理的几大周期介绍

Node.js Event Loop 处理的几大周期如下图所示&#xff1a; Timer&#xff1a;通过 setTimeout() 或 setInterval() 安排的一切都将在这里处理。 IO 回调&#xff1a;这里将处理大部分回调。 由于 Node.js 中的所有用户态代码基本上都在回调中&#xff08;例如&#xff0c;对传…
阅读更多...
深入理解机器学习——概率图模型（Probabilistic Graphical Model）：马尔可夫随机场（Markov Random Field，MRF）

深入理解机器学习——概率图模型（Probabilistic Graphical Model）：马尔可夫随机场（Markov Random Field，MRF）

分类目录&#xff1a;《深入理解机器学习》总目录 马尔可夫随机场&#xff08;Markov Random Field&#xff0c;MRF&#xff09;是典型的马尔可夫网&#xff0c;这是一种著名的无向图模型&#xff0c;图中每个结点表示一个或一组变量&#xff0c;结点之间的边表示两个变量之间的…
阅读更多...
Zookeper报错：Will not attempt to authenticate using SASL (unknown error)|防火墙的问题

Zookeper报错：Will not attempt to authenticate using SASL (unknown error)|防火墙的问题

先放一张debug成功的图吧~ 之前一直报这个错&#xff0c;不知道为什么&#xff0c;非常迷惑&#xff0c;然后试了多方法&#xff0c;就是防火墙的问题。我是Hadoop2.5和centos6&#xff0c;因此没法用systemtcl&#xff0c;就使用serive命令。 方式一&#xff1a;Linux命令来…
阅读更多...
Kubernetes单主集群的部署（一）

Kubernetes单主集群的部署（一）

目录 一、k8s单主架构集群的部署 1.操作系统初始化配置 2.部署 etcd 集群 3.部署docker引擎 4.部署 Master 组件 5.部署 Worker Node 组件 6.部署网络组件&#xff08;使用 flannel&#xff09; 一、k8s单主架构集群的部署 k8s集群master01&#xff1a;192.168.116.1…
阅读更多...
纯手写2022年最新JVM调优实战手册，看完让你精通JVM调优

纯手写2022年最新JVM调优实战手册，看完让你精通JVM调优

很多程序员不重视 JVM 内存调优&#xff0c;写出来的代码经常出现 OOM 等内存问题。而且&#xff0c;面试求职者中&#xff0c;很多求职者一旦遇到JVM 或者 JVM 调优方面的问题&#xff0c;往往不知如何回答&#xff0c;才能充分展现自己的能力。 jvm OOM问题实战分析 说说问题…
阅读更多...
JS 原生面经从初级到高级【近1.5W字】

JS 原生面经从初级到高级【近1.5W字】

前言 是时候撸一波 JS 基础啦,撸熟了,银十速拿 offer; 本文不从传统的问答方式梳理,而是从知识维度梳理,以便形成知识网络; 包括函数,数组,对象,数据结构,算法,设计模式和 http. 1. 函数 1.1函数的3种定义方法 1.1.1 函数声明 //ES5 function getSum(){} function (){}//匿名…
阅读更多...
【MATLAB教程案例56】VGG16网络的MATLAB编程学习和实现，以步态识别为例进行仿真分析

【MATLAB教程案例56】VGG16网络的MATLAB编程学习和实现，以步态识别为例进行仿真分析

欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》 目录 1.软件版本 2.VGG16理论概述
阅读更多...
ADI Blackfin DSP处理器-BF533的开发详解12：Memory DMA的使用详解（含源代码）

ADI Blackfin DSP处理器-BF533的开发详解12：Memory DMA的使用详解（含源代码）

硬件准备 ADSP-EDU-BF533&#xff1a;BF533开发板 AD-HP530ICE&#xff1a;ADI DSP仿真器 软件准备 Visual DSP软件 硬件链接 接口功能介绍 MDMA 全称是 memoryDMA &#xff0c;是内存到内存搬运数据的 DMA。在 DSP 做算法时&#xff0c;经常会遇到数据重组或者搬移&#…
阅读更多...
谁说菜鸟不会数据分析 | 学习笔记（全）

谁说菜鸟不会数据分析 | 学习笔记（全）

一.前言 数据分析是为了提取有用信息和形成结论而对数据加以详细研究和概括总结的过程 数据分析的目的是把隐藏在一大批看似杂乱无章的数据背后的信息集中和提炼出来&#xff0c;总结出所研究对象的内在规律。在实际工作中&#xff0c;数据分析能够帮助管理者进行判断和决策&…
阅读更多...
Linux | 进程信号 | 信号的产生 | 进程处理信号过程 | 进程pending，block，handler设置 | 用户态、内核态

Linux | 进程信号 | 信号的产生 | 进程处理信号过程 | 进程pending，block，handler设置 | 用户态、内核态

文章目录信号的概念Ctrl C信号Linux中的信号信号产生前由终端产生信号由软件条件产生信号硬件异常产生信号core dump信号产生时sigset_tsigprocmask信号产生后用户态和内核态sigaction信号的概念 在日常生活中&#xff0c;我们看到绿灯选择过马路&#xff0c;看到红灯选择等待…
阅读更多...
浅谈Java Web经典三层架构和MVC框架模式

浅谈Java Web经典三层架构和MVC框架模式

从前端到后端整体架构做一个分析&#xff0c;通过这个分析更清楚的了解一下具体的前后端架构。以下三个架构属于三种架构&#xff0c;有共同点&#xff0c;但是并不是从属关系。 01 MVC模型 MVC是一种模型概念&#xff0c;绝大多数架构都是根据他来实现的&#xff0c;但是并不…
阅读更多...
使用Docker+Jenkins+Gitee自动化部署Vue+ElementUI项目

使用Docker+Jenkins+Gitee自动化部署Vue+ElementUI项目

参考本文章并打算跟着步骤进行构建部署的朋友们&#xff0c;建议直接先看踩坑总结&#xff0c;看看自己是否存在对应的问题&#xff0c;免得构建完才发现出错了&#xff0c;毕竟构建一次过程还挺长的。也可以自己走一遍后再参考如何解决啦。 1、Docker安装Jenkins 关于如何安…
阅读更多...
使用 Monai 和 PyTorch 预处理 3D Volumes以进行肿瘤分割

使用 Monai 和 PyTorch 预处理 3D Volumes以进行肿瘤分割

1.介绍 针对在使用传统图像处理工具时可能遇到的困难&#xff0c;深度学习已成为医疗保健领域的主要解决方案。 因为医学图像比标准图像更难处理&#xff08;高对比度、人体的广泛变化……&#xff09;深度学习用于分类、对象检测&#xff0c;尤其是分割任务。 在分割方面&a…
阅读更多...
[附源码]计算机毕业设计健身生活系统论文Springboot程序

[附源码]计算机毕业设计健身生活系统论文Springboot程序

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
SQL注入漏洞 | updatexml报错注入

SQL注入漏洞 | updatexml报错注入

文章目录前言MySQL updatexml报错注入前言 XML XML 被设计用来传输和存储数据&#xff0c;是各种应用程序之间进行数据传输的最常用的工具。 xpath XPath 是一门在 XML 文档中查找信息的语言。XPath 使用路径表达式来选取 XML 文档中的节点或者节点集。这些路径表达式和我们在…
阅读更多...
传统机器学习算法-支持向量机模型详解

传统机器学习算法-支持向量机模型详解

原文链接 引言 本篇我们要讲解的模型是大名鼎鼎的支持向量机 SVM&#xff0c;这是曾经在机器学习界有着近乎「垄断」地位的模型&#xff0c;影响力持续了好多年。直至今日&#xff0c;即使深度学习神经网络的影响力逐渐增强&#xff0c;但 SVM 在中小型数据集上依旧有着可以和…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023