时间复杂度

$O(logn)$

三个模板

整数二分（两个）

int 答案右区间(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (在答案区间(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

// ###############################################

int 答案左区间(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (在答案区间(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

浮点二分

double 浮点二分(double l, double r)
{
	double eps = 1e-6;
    while (l + eps < r)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

两个整数二分模板的记忆

答案在右区间

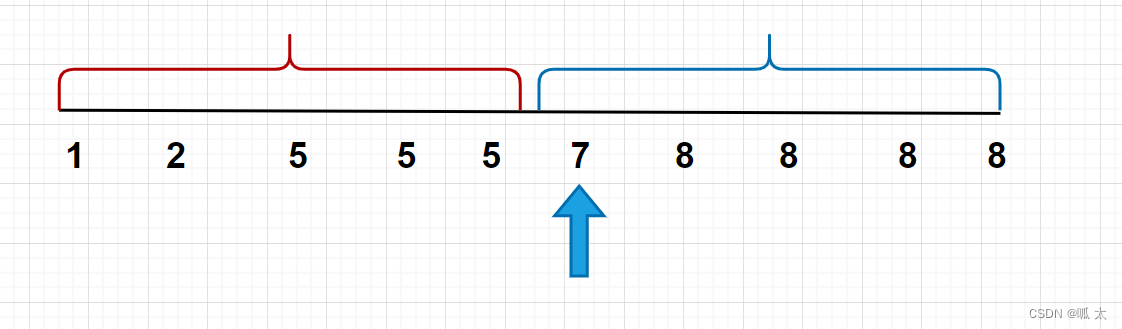
现有如图所示的区间，我们现在给出目标：找到第一个大于5的元素，
（关键要素：大于5）
根据这个关键要素，我们可以得到一个满足条件的区间，我们的答案也就在这个区间内。对应图中的蓝色区间，所以我们选用第一个模板。

这里的 check() 函数，对应的就是是否满足蓝色区间。

因为我们的答案只会出现在边界位置，即蓝色箭头，所以我们每次更新区间，（l，r指针）往蓝色箭头靠。
那么，什么时候移动l，r指针？很简单，我们的mid在哪个区间，我们移动哪个指针！

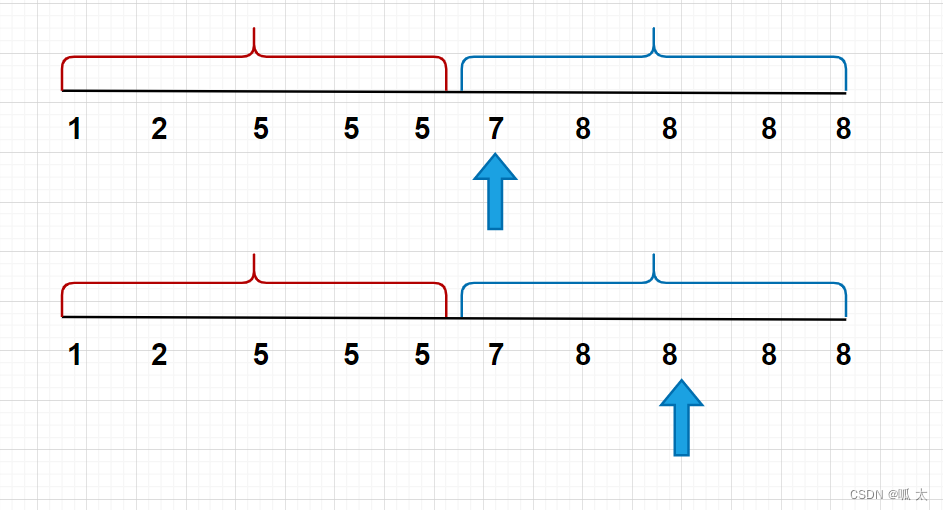
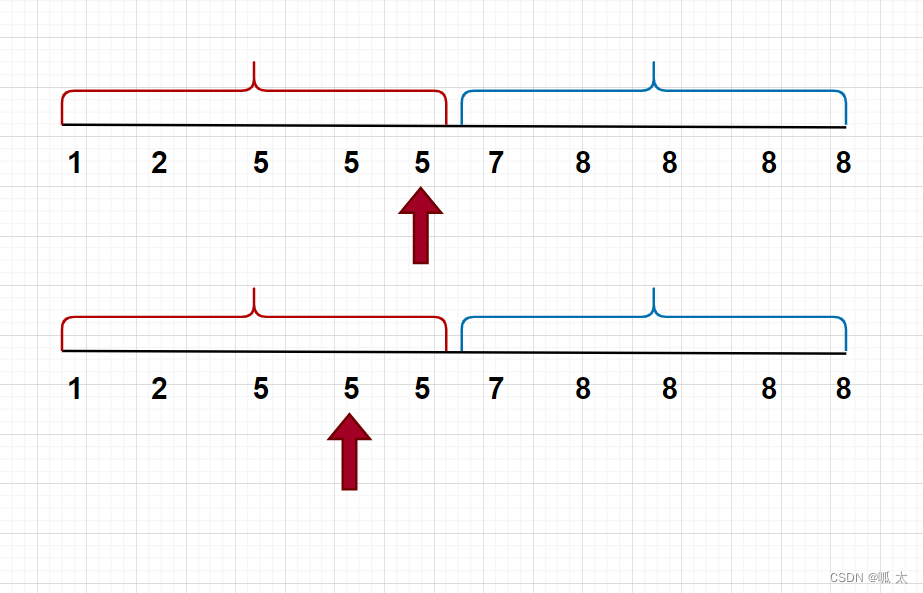
1. r=mid：
   如下图，我们的mid，可能落在如下两个位置，因为mid在答案区间（右区间），所以我们移动r指针 r=mid。（为什么mid不需要减一？当mid为8时，因为不是答案我们可以减一，但是当mid为7时，我们减一，区间就指向5了，我们错过了正确答案，所以我们不能减一。也就是当mid在答案区间，mid可能直接就是答案了，所以我们直接把答案mid赋值过去）
   

2. l=mid+1：
   同理，当我们在左边区间，无论mid在哪，mid本身不可能是答案，所以我们没必要把mid留在区间内，可以多往后移动一格即mid+1，而mid+1刚好可能是答案
   

3. 所以，我们在赋值的时候，直接考虑mid刚好在两个区间边界位置即可

答案在左区间

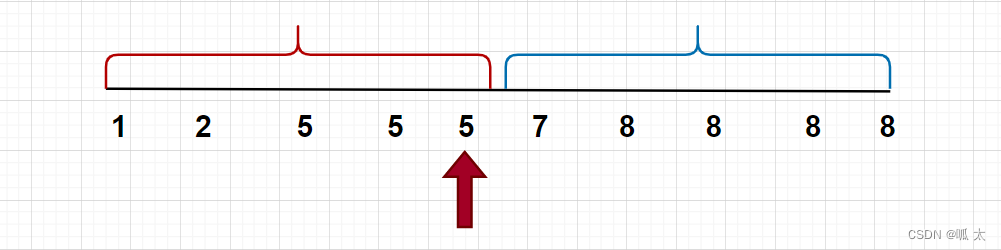
当我们需要寻找最后一个小于等于5，我们可以得到红色答案区间。

下面的方法都一样了：

1. l=mid：
   当mid在左区间，我们需要更新l指针，mid可能正好是答案，所以直接l=mid。
2. r=mid-1：
   当mid在右区间，我们更新r指针，mid-1可能是答案，所以r=mid-1
   

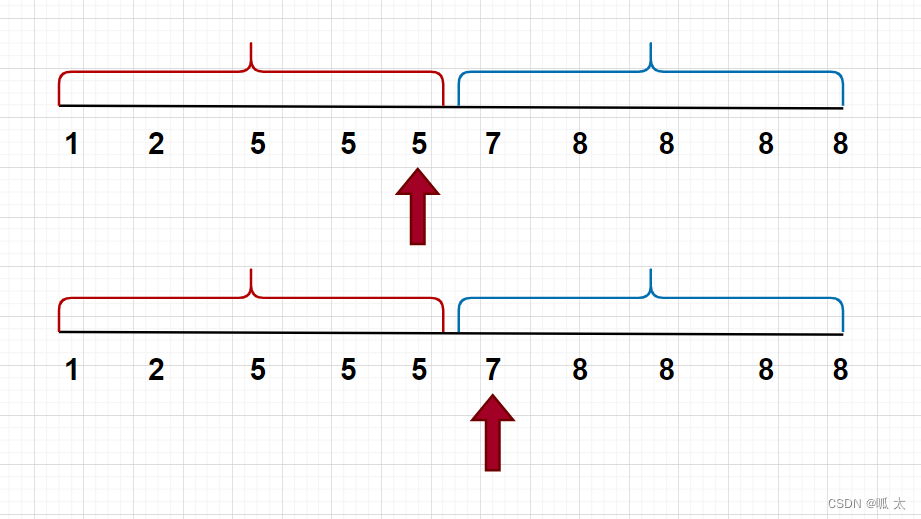
那么，mid = l + r >> 1还是mid = l + r + 1 >> 1 ？
什么时候+1？
可以用以下方法记忆：

• 有-必有+
• 答案在左区间容易死循环，让mid多加个一跑去右区间去