（中等）LeetCode146 LRU 缓存 Java

news2024/11/26 20:25:02

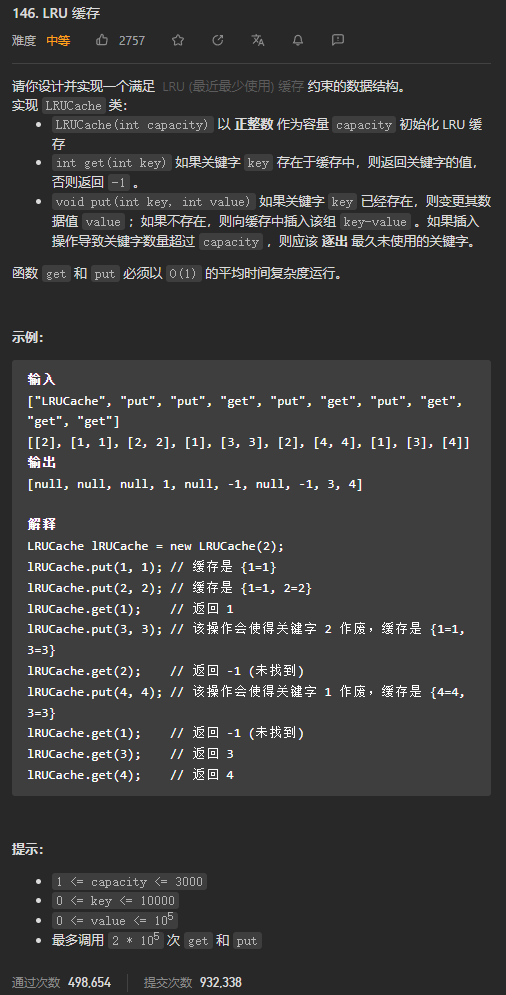
在这里插入图片描述
本题有两种实现操作，需要使用到一个哈希表和一个双向链表。在Java语言中，有一种结合了哈希表和双向链表的数据结构，LinkedHashMap

import java.util.LinkedHashMap;
import java.util.Map;

class LRUCache extends LinkedHashMap<Integer, Integer> {

    private int capacity;

    public LRUCache(int capacity) {
        super(capacity, 0.75f, true);
        this.capacity = capacity;
    }

    public int get(int key) {
        return super.getOrDefault(key, -1);
    }

    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity;
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

LRU缓存机制可以通过哈希表辅以双向链表实现，需要使用一个哈希表和一个双向链表维护所有在缓存中的键值对。

双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。
哈希表即为普通的哈希映射，通过缓存数据的键映射到其在双向链表中的位置

这样，首先使用哈希表进行定位，找出缓存项在双向链表中的位置，随后将其移动到双向链表的头部，即可在O(1)时间内完成get或者put操作，具体方法如下：

对于get操作，首先判断key是否存在：
- 如果key不存在，则返回-1
- 如果key存在，则key对应的节点是最近被使用的节点，通过哈希表定位到该节点在双向链表中的位置，并将其移动到双向链表的头部，最后返回该节点的值
对于put操作，首先判断key是否存在：
- 如果key不存在，使用key和value创建一个新的节点，在双向链表的头部添加该节点，并将key和该节点添加进哈希表中。然后判断双向链表中的节点数是否超出容量，如果超出容量，则删除双向链表的尾部节点，并删除哈希表中对应的项
- 如果key存在，则与get操作类似，先通过哈希表定位，再将对应的节点的值更新为value，并将该节点移到双向链表的头部

上述各项操作中，访问哈希表的时间复杂度为O(1)，在双向链表的头部添加节点，在双向链表的尾部删除节点的复杂度也为O(1)。而将一个节点移动到双向链表的头部，可以分成【删除该节点】和【在双向链表的头部添加节点】两步操作，都可以在O(1)的时间内完成。

import java.util.HashMap;
import java.util.Map;

class LRUCache {


    private Map<Integer, DLinkedNode> cache = new HashMap<>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;


    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        //如果key存在，则通过哈希表定位，再移到头部
        moveToHead(node);
        return node.val;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            //如果key不存在，创建一个新的节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            //添加进哈希表
            cache.put(key, newNode);
            //添加值双向链表头部
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                DLinkedNode tail = removeTail();
                //如果超出容量，删除双向链表尾部节点
                cache.remove(tail.key);
                --size;
            }
        } else {
            //如果key存在，先通过哈希表定位，再修改value的值，并移到头部
            node.val = value;
            moveToHead(node);
        }
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private DLinkedNode removeTail() {
        DLinkedNode node = tail.prev;
        removeNode(node);
        return node;
    }

    private void addToHead(DLinkedNode node) {
        node.next = head.next;
        node.prev = head;
        head.next.prev = node;
        head.next = node;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }
}

class DLinkedNode {
    int key;
    int val;
    DLinkedNode prev;
    DLinkedNode next;

    public DLinkedNode() {

    }

    public DLinkedNode(int key, int val) {
        this.key = key;
        this.val = val;
    }
}