前向传播（forward propagation或forward pass）指的是：按顺序（从输⼊层到输出层）计算和存储神经⽹络中每层的结果。

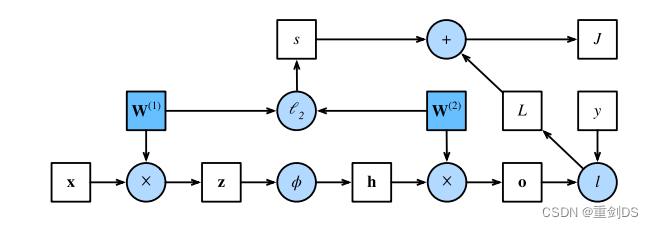
绘制计算图有助于我们可视化计算中操作符和变量的依赖关系。下图是与上述简单⽹络相对应的计算图， 其中正⽅形表⽰变量，圆圈表⽰操作符。左下⻆表⽰输⼊，右上⻆表⽰输出。注意显⽰数据流的箭头⽅向主要是向右和向上的。

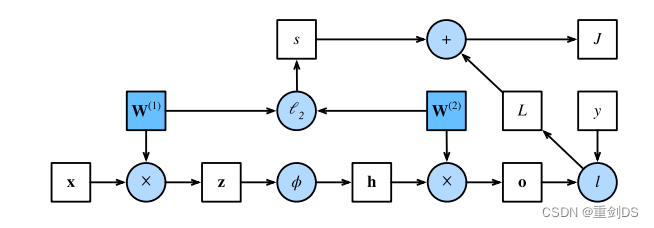
反向传播（backward propagation或backpropagation）指的是计算神经⽹络参数梯度的⽅法。简⾔之，该⽅法根据微积分中的链式规则，按相反的顺序从输出层到输⼊层遍历⽹络。

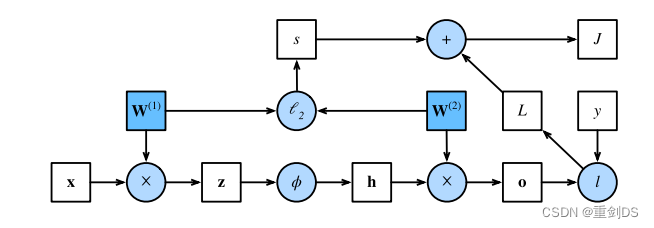
根据这个计算图，在计算图中的单隐藏层简单⽹络的参数是 W(1)和W(2)。反向传播的⽬的是计算梯度∂J/∂W(1)和 ∂J/∂W(2)。为此，我们应⽤链式法则，依次计算每个中间变量和参数的梯度。计算的顺序 与前向传播中执⾏的顺序相反，因为我们需要从计算图的结果开始，并朝着参数的⽅向努⼒。

第⼀步是计算 ⽬标函数J = L + s相对于损失项L和正则项s的梯度。

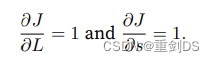
接下来，我们根据链式法则计算⽬标函数关于输出层变量o的梯度：

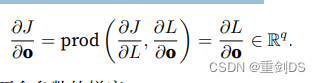这里用到了第一步计算的结果。

prod 的全称是 "product",在数学和计算机科学中，它通常表示两个或多个数的乘积。例如，如果有两个数 a 和 b,那么它们的乘积可以表示为 a * b,也可以写成 prod(a, b)。在反向传播算法中，prod 是一个运算符，用于计算多个张量(或矩阵)的乘积。

例如，假设我们有两个张量 A 和 B:

A = [[1, 2], [3, 4]]

B = [[5, 6], [7, 8]]

   

那么 A * B 就是：

A * B = [[1*5+2*7, 1*6+2*8], [3*5+4*7, 3*6+4*8]]

= [[17, 26], [39, 50]]

在这个例子中，prod 运算符将两个二维张量相乘。

接下来，我们计算正则化项相对于两个参数的梯度：

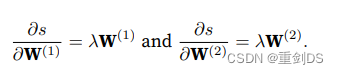
现在我们可以计算最接近输出层的模型参数的梯度 ∂J/∂W(2) ∈ Rq×h，因为在计算图中W(2)比W(1)接近输出层o，所以W(2)说成最接近没错的，然后使⽤链式法则得出：

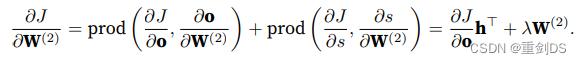
为了获得关于W(1)的梯度，我们需要继续沿着输出层到隐藏层反向传播。关于隐藏层输出的梯度∂J/∂h ∈ Rh由下式给出：

由于激活函数ϕ是按元素计算的，计算中间变量z的梯度∂J/∂z ∈ Rh 需要使⽤按元素乘法运算符，我们⽤⊙表示：

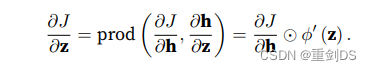
最后，我们可以得到最接近输⼊层的模型参数的梯度 ∂J/∂W(1) ∈ Rh×d。根据链式法则，我们得到：

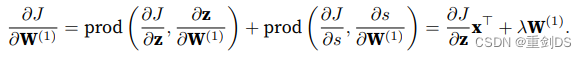
因此，在训练神经⽹络时，在初始化模型参数后，我们交替使⽤前向传播和反向传播，利⽤反向传播给出的 梯度来更新模型参数。注意，反向传播重复利⽤前向传播中存储的中间值，以避免重复计算。我的理解是类似于高数里面的求导公式，f’(x)=lim…=某个带有x的公式，但是这个x是未知数，还得带入前向传播计算后存储的中间值x才能算出具体的导数值，也就是梯度值。带来的影响之⼀是我们需要保留中间值，直到反向传播完成。这也是训练⽐单纯的预测需要更多的内存（显存）的原因之⼀，因为预测只需要进行前向传播即可，我们不需要更新参数，因此也不需要进行反向传播。

---

p168练习

1. 假设⼀些标量函数X的输⼊X是n × m矩阵。f相对于X的梯度维数是多少？

答：对于一个标量函数f，相对于输入矩阵X的梯度维数应该是与X具有相同的维数，即n × m。

举个例子，假设我们有一个标量函数f，定义如下：

f(X) = sum(X)

其中，X是一个3×2的矩阵：

X = [[1, 2],
[3, 4],
[5, 6]]

将所有元素相加得到：

f(X) = 1 + 2 + 3 + 4 + 5 + 6 = 21

函数f计算输入矩阵X的所有元素的和。现在，我们将计算函数f相对于输入矩阵X的梯度。

由于函数f是对输入矩阵X的所有元素求和，f(X) 相对于X的梯度将是一个与X具有相同维度的矩阵，称为Jacobian矩阵。在这个例子中，梯度的维数是3×2的矩阵，与输入矩阵X相同：

∇f(X) = [[1, 1],
[1, 1],
[1, 1]]

每个元素都是1，表示在函数f的输出对每个输入元素的微小变化中，对应位置的偏导数。由于函数f对输入矩阵的每个元素都有相同的贡献，因此所有偏导数都是1。

4. 假设想计算⼆阶导数。计算图发⽣了什么？预计计算需要多⻓时间？

答：当计算模型的二阶导数时，计算图会发生以下变化：

1. 在正向传播过程中，需要保留一阶导数的中间结果。这些中间结果将在反向传播过程中用于计算二阶导数。
2. 在反向传播过程中，需要计算一阶导数的梯度以及二阶导数的梯度。具体而言，需要计算二阶导数对于模型参数的梯度、二阶导数对于一阶导数的梯度。

预计计算二阶导数需要更多的计算量和内存消耗，因为需要保留和计算更多的中间结果。

时间开销方面，计算二阶导数的时间会比计算一阶导数更长。具体时间将取决于模型的结构和参数数量、样本数量以及所用的计算设备性能。由于计算二阶导数涉及更多的计算和内存操作，可能需要更长的时间。

需要注意的是，计算二阶导数可能会导致计算资源的需求增加，尤其是在参数量大、模型复杂度高的情况下。在实际应用中，评估计算时间和内存消耗是很重要的，可以考虑使用近似方法或优化技术来降低计算二阶导数的成本。

综上所述，计算二阶导数需要更多的计算量和内存消耗，预计会比计算一阶导数花费更长的时间。具体的时间和内存消耗取决于模型和计算设备的特性。

5. . 假设计算图对当前拥有的GPU来说太⼤了。

1. 请试着把它划分到多个GPU上。

2. 与⼩批量训练相⽐，有哪些优点和缺点？

答：

1. 划分计算图到多个GPU上：
   •  在划分计算图到多个GPU上时，一种常见的方法是使用数据并行ism，即将数据划分为多个小批量，每个小批量分配到不同的GPU上进行计算。
   •  每个GPU上的计算图副本可以执行前向传播和反向传播，并将计算结果传递给主GPU，主GPU则负责聚合各个GPU的计算结果以更新模型参数。

2. 与小批量训练相比，划分计算图到多个GPU上有以下一些优点和缺点：

优点：

• 并行计算：多个GPU可以同时执行计算，加速整体计算过程，尤其是在大型模型和大规模数据集上。
• 内存消耗减小：将计算图分散到多个GPU上，可以减小单个GPU的内存需求，使得可以处理更大规模的模型和数据。
• 分布式训练：通过多个GPU并行计算，可以实现分布式训练，提高训练效率和扩展性。

缺点：

• 通信开销：在多个GPU之间传输数据和计算结果需要一定的通信开销，可能会导致一些额外的延迟。
• 实现复杂性：划分计算图和实现多GPU的并行计算需要一些额外的编程和调试工作，相对于单GPU训练，实现复杂性较高。
• GPU资源需求：多个GPU的使用需要具备多个GPU的硬件资源，如果可用的GPU资源有限，则可能无法充分利用这种并行计算的优势。

综上所述，划分计算图到多个GPU上可以加速计算过程和扩展训练规模，但需要权衡计算和通信开销以及可用的GPU资源。适用于大规模模型和数据集以及具备足够GPU资源的情况。