一、35. 搜索插入位置

1.题目简介

35. 搜索插入位置
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
在这里插入图片描述

2.解题思路

3.代码

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while(left <= right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] < target)
            {
                left = mid + 1;
            }
            else if(nums[mid] > target)
            {
                right = mid - 1;
            }
            else
            {
                return mid;
            }
        }
        return left;
    }
};

4.运行结果

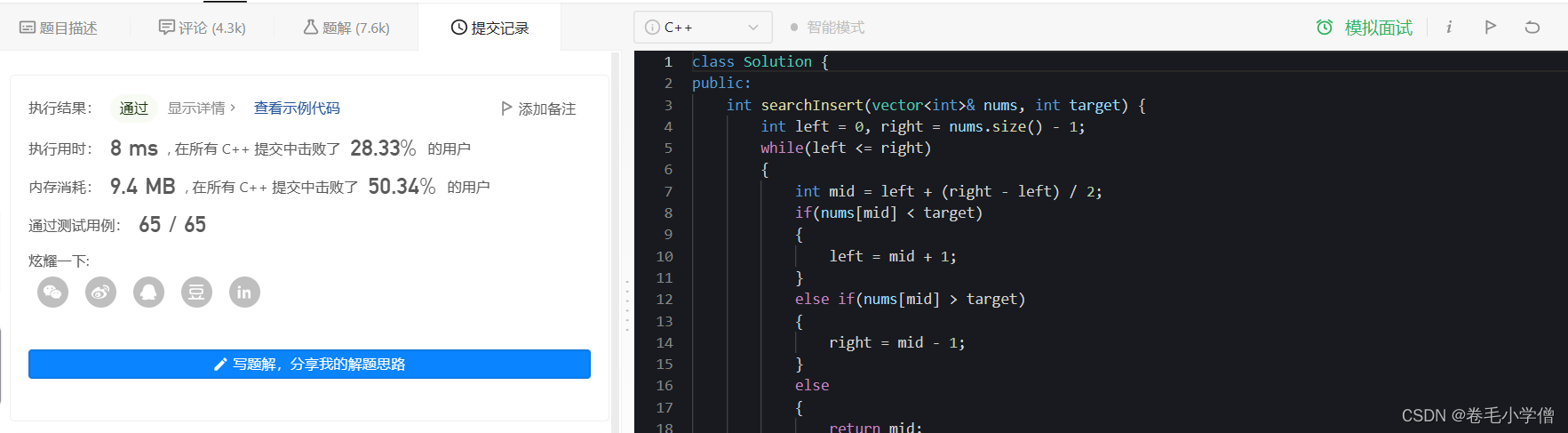
在这里插入图片描述

二、69. x 的平方根

1.题目简介

69. x 的平方根
给你一个非负整数 x ，计算并返回 x 的算术平方根。
由于返回类型是整数，结果只保留整数部分，小数部分将被舍去。
注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。
在这里插入图片描述

2.解题思路

3.代码

class Solution {
public:
    int mySqrt(int x) {
        if(x < 1) return 0;
        int left = 1, right = x;
        while(left < right)
        {
            long long mid = left + (right - left + 1) / 2;
            if(mid * mid <= x)
            {
                left = mid;
            }
            else
            {
                right = mid - 1;
            }
        }
        return left;
    }
};

4.运行结果

在这里插入图片描述

三、852. 山脉数组的峰顶索引

1.题目简介

852. 山脉数组的峰顶索引
符合下列属性的数组 arr 称为山脉数组：
arr.length >= 3
存在 i（0 < i < arr.length - 1）使得：
arr[0] < arr[1] < … arr[i-1] < arr[i]
arr[i] > arr[i+1] > … > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ，返回满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
在这里插入图片描述

2.解题思路

3.代码

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
        int left = 1, right = arr.size() - 2;
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(arr[mid] > arr[mid - 1])//如果mid所处位置是上升的，则我们要在mid + 1~right区间寻找
            {
                left = mid;
            }
            else//如果mid所处位置是下降的，则我们要在left~mid-1区间寻找
            {
                right = mid - 1;
            }
        }
        return left;
    }
};