我们经常使用微分运动学来计算机器人的逆运动学，对于单个任务的机械臂的逆运动学使用的是梯度投影法：

冗余机械臂求解逆运动学解——梯度投影法

但是对于多任务的逆运动学在一般的机器人学里面很少有提及，最近看到了相关的论述，于是做一下笔记整理一下。

前置说明

设共有$n_t$个任务，对于每个任务$tas{k}_i$我们可以给出其雅克比矩阵和期望的速度的表示：

t a s k i : = { J i , w i ∗ } . \begin{align} {task}_{i}: & = \left\{\mathbf{J}_{i}, \mathbf{w}_{i}^{*}\right\} . \end{align} taski​:​={Ji​,wi∗​}.​​

我们怎么计算这里的逆运动学呢？即根据一系列的${\mathbf{w}}_i$来计算$\dot{\mathbf{q}}$呢？我们可以分为无优先级和有优先级的两种情况来考虑。

1. 多任务（优先级同等）

优先级是同等的情况下，我们可以建立关节空间($\dot{\mathbf{q}}$)和操作空间($\overline{\mathbf{w}}$)之间的映射

$$\begin{array}{rl}\underset{\overline{\mathbf{J}}}{\underbrace{\left[\begin{array}{c}{\mathbf{J}}_1\\ ⋮\\ {\mathbf{J}}_{n_t}\end{array}\right]}}\dot{\mathbf{q}}& =\underset{\overline{\mathbf{w}}}{\underbrace{\left(\begin{array}{c}{\mathbf{w}}_1^{}\\ ⋮\\ {\mathbf{w}}_{n_t}^{}\end{array}\right)}}\end{array}$$
直接对上面的方程求伪逆就可以了。

$$\begin{array}{rl}\dot{\mathbf{q}}& =\underset{\overline{\mathbf{J}}}{\underbrace{{\left[\begin{array}{c}{\mathbf{J}}_1\\ ⋮\\ {\mathbf{J}}_{n_t}\end{array}\right]}^{+}}}\underset{\overline{\mathbf{w}}}{\underbrace{\left(\begin{array}{c}{\mathbf{w}}_1^{\ast }\\ ⋮\\ {\mathbf{w}}_{n_t}^{\ast }\end{array}\right)}}\end{array}$$

一种排优先级的方式是引入一个权重矩阵：

$$\begin{array}{rl}{\overline{\mathbf{J}}}^{+W}& ={\left({\overline{\mathbf{J}}}^T\mathbf{W}\overline{\mathbf{J}}\right)}^{-1}{\overline{\mathbf{J}}}^T\mathbf{W}\end{array}$$

其中：

$$\mathbf{W}=\mathrm{diag}\left(w_1,\dots ,w_m\right)$$

这等价于计算下面表达式的最小值

$${\Vert {\mathbf{W}}^{1/2}(\overline{\mathbf{w}}-\overline{\mathbf{J}}\dot{\mathbf{q}})\Vert }_2$$

对于没有优先级的情况我们可以看到上面的对角矩阵$\mathbf{W}$的对角元都是1。

2. 多任务（存在优先级）

优先级的意思就是，我们优先保证某个任务的实现，其他任务的实现度可以相对较差。我们不妨从两个任务的情况来看。

2.1 简单案例引入：两任务情况

关于第一个任务我们有：

$$\begin{array}{rl}\dot{\mathbf{q}}& ={\mathbf{J}}_1^{†}{\mathbf{w}}_1^{\ast }+{\mathbf{N}}_1{\dot{\mathbf{q}}}_0\end{array}$$

对于第二个任务我们代入(5)式有：

$$\begin{array}{r}{\mathbf{w}}_2={\mathbf{J}}_2\dot{\mathbf{q}}={\mathbf{J}}_2\left({\mathbf{J}}_1^{†}{\mathbf{w}}_1^{\ast }+{\mathbf{N}}_1{\dot{\mathbf{q}}}_0\right)\end{array}$$

这样我们可以解出${\dot{\mathbf{q}}}_0$

$$\begin{array}{rl}{\dot{\mathbf{q}}}_0& ={\left({\mathbf{J}}_2{\mathbf{N}}_1\right)}^{†}\left({\mathbf{w}}_2^{\ast }-{\mathbf{J}}_2{\mathbf{J}}_1^{+}{\mathbf{w}}_1^{\ast }\right)\end{array}$$

于是我们带回(5)式

$$\begin{array}{rl}\dot{\mathbf{q}}& ={\mathbf{J}}_1^{†}{\mathbf{w}}_1^{\ast }+{\mathbf{N}}_1{\left({\mathbf{J}}_2{\mathbf{N}}_1\right)}^{†}\left({\mathbf{w}}_2^{\ast }-{\mathbf{J}}_2{\mathbf{J}}_1^{+}{\mathbf{w}}_1^{\ast }\right)\end{array}$$

这样我们就用一个表达式把$$\dot{\mathbf{q}}$和第一个任务的期望的速度${\mathbf{w}}_1$和第二个任务的期望的速度${\mathbf{w}}_2$联系了起来。只用一个式子就进行了表示。

那么如果我们有更多的任务我们应该怎么表示呢？我们可以定义一个变换：

$$\begin{array}{rl}{\overline{\mathbf{J}}}_i& =\left[\begin{array}{c}{\mathbf{J}}_1\\ ⋮\\ {\mathbf{J}}_{i-1}\end{array}\right]\end{array}$$

而${\overline{\mathbf{N}}}_i$是${\overline{\mathbf{J}}}_i$对应的零空间，零空间的含义即：

$$\begin{array}{rl}{\overline{\mathbf{J}}}_i{\overline{\mathbf{N}}}_i& =0\end{array}$$

对于${\overline{\mathbf{J}}}_1$为单位矩阵$\mathbf{E}$。那么我们可以把式(8)写作

$$\begin{array}{rl}\dot{\mathbf{q}}& ={\overline{\mathbf{N}}}_1{\dot{\mathbf{q}}}_1+{\overline{\mathbf{N}}}_2{\dot{\mathbf{q}}}_2\end{array}$$

其中

$$\begin{array}{rl}{\overline{\mathbf{N}}}_1& =\mathbf{E}\\ {\dot{\mathbf{q}}}_1& ={\mathbf{J}}_1^{†}{\mathbf{w}}_1^{\ast }\\ & ={\left({\mathbf{J}}_1{\overline{\mathbf{N}}}_1\right)}^{†}\left({\mathbf{w}}_1^{\ast }\right)\\ {\overline{\mathbf{N}}}_2& ={\mathbf{N}}_1\\ {\dot{\mathbf{q}}}_2& ={\left({\mathbf{J}}_2{\mathbf{N}}_1\right)}^{†}\left({\mathbf{w}}_2^{\ast }-{\mathbf{J}}_2{\mathbf{J}}_1^{+}{\mathbf{w}}_1^{\ast }\right)\\ & ={\left({\mathbf{J}}_2{\overline{\mathbf{N}}}_2\right)}^{†}\left({\mathbf{w}}_2^{\ast }-{\mathbf{J}}_2{\overline{\mathbf{N}}}_1{\dot{\mathbf{q}}}_1\right)\end{array}$$

2.2 多任务情况

我们可以发现规律：

单个任务的时候计算逆运动学采用梯度投影法，而增加一个任务$tas{k}_i$可以用前面的任务来生成新的${\overline{\mathbf{N}}}_i$和${\overline{\mathbf{q}}}_i$。类似于递推的原理，我们要根据前面的几个优先的任务$tas{k}_1$-$tas{k}_{i-1}$得到的来推导出接下来的引入$tas{k}_i$，如果前面的$1$ ~ $i-1$的任务我们可以得到它们表示的$\dot{\mathbf{q}}$

$$\begin{array}{r}\dot{\mathbf{q}}=\sum _{k=1}^{i-1}{\overline{\mathbf{N}}}_k{\dot{\mathbf{q}}}_k\end{array}$$

我们引入一个新任务进行扩展：

$$\begin{array}{r}\dot{\mathbf{q}}=\sum _{k=1}^{i-1}{\overline{\mathbf{N}}}_k\dot{{\mathbf{q}}_k}+{\overline{\mathbf{N}}}_i{\dot{\mathbf{q}}}_i\end{array}$$

我们根据第$i$个任务的微分运动并且代入(11)式有：

$${\mathbf{w}}_i={\mathbf{J}}_i\dot{\mathbf{q}}={\mathbf{J}}_i\left(\sum _{k=1}^{i-1}{\overline{\mathbf{N}}}_k\dot{{\mathbf{q}}_k}+{\overline{\mathbf{N}}}_i{\dot{\mathbf{q}}}_i\right)$$

于是我们可以得到：

$$\begin{array}{r}{\dot{\mathbf{q}}}_i={\left({\mathbf{J}}_i{\overline{\mathbf{N}}}_i\right)}^{+}\left({\mathbf{w}}_i^{\ast }-{\mathbf{J}}_i\sum _{k=1}^{i-1}{\overline{\mathbf{N}}}_k{\dot{\mathbf{q}}}_k\right)\end{array}$$

这就是最后的总的公式：

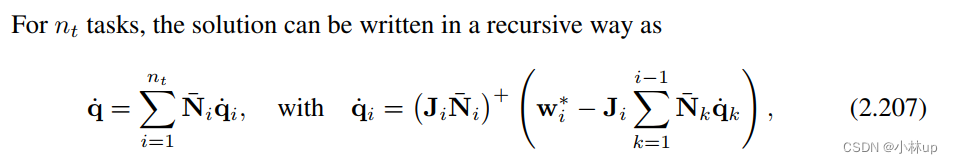
3. 例子

3.1 单任务

如图平面的三自由度的机械臂，机械臂的长度都是1($l_0,l_1,l_2,l_3$)，我们在$t$时刻观测到关节角度为${\mathbf{q}}_t=(\pi /6,\pi /3,\pi /3{)}^T$，这时候的末端的速度为${}_0{\dot{\mathbf{r}}}_{E,t}^{\ast }=(1,1{)}^T$，求解这时候的各关节的角速度？

---

解答：
期望速度为：

$${\mathbf{w}}_{E,t}^{\ast }={}_0{\dot{\mathbf{r}}}_{E,t}^{\ast }=\left(\begin{array}{l}1\\ 1\end{array}\right)$$

对于${\mathbf{q}}_t=(\pi /6,\pi /3,\pi /3)$，我们可以计算它的雅克比矩阵,公式为：

$$\begin{gathered} \begin{array}{rl}{\mathbf{J}}_{eAP}(\mathbf{q})& =\left[\begin{array}{ccc}{l}_1{c}_1+l_2{c}_{12}+l_3{c}_{123}& l_2{c}_{12}+l_3{c}_{123}& l_3{c}_{123}\\ -l_1{s}_1-l_2{s}_{12}-l_3{s}_{123}& -l_2{s}_{12}-l_3{s}_{123}& -l_3{s}_{123}\end{array}\right]\end{array} \\ \text{其中 }{c}_{123}=\cos \left(q_1+q_2+q_3\right)s_{123}=\sin \left(q_1+q_2+q_3\right) \end{gathered}$$

于是我们有：

$${\mathbf{J}}_{E,t}={\mathbf{J}}_E\left({\mathbf{q}}_t\right)=\frac{1}{2}\left[\begin{array}{ccc}0& -\sqrt{3}& -\sqrt{3}\\ -4& -3& -1\end{array}\right]$$

通过计算伪逆的方法我们可以得到：

$${\dot{\mathbf{q}}}_t^{\text{single }}={\mathbf{J}}_{E,t}^{+}{\mathbf{w}}_{E,t}^{\ast }=\left(\begin{array}{c}0.069\\ -0.560\\ -0.595\end{array}\right)$$

我们可以把这个结果带回去我们发现是符合末端的速度的要求的。

$${\mathbf{w}}_{E,t}={\mathbf{J}}_{E,t}{\dot{\mathbf{q}}}_t^{\text{single }}=\left(\begin{array}{l}1\\ 1\end{array}\right)={\mathbf{w}}_{E,t}^{\ast }$$

3.2 多任务（优先级同等）

除了前面定义的末端速度的任务，我们再额外定义一个任务：我们要求前面两个关节的速度为0：

$${\mathbf{w}}_j=\left(\begin{array}{l}0\\ 0\end{array}\right),{\mathbf{J}}_j=\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\end{array}\right]$$

在添加这个条件的情况下，我们再计算一下关节空间的角速度。

解答：
我们根据前面的多任务逆运动学情况有：

$$\dot{\mathbf{q}}={\left[\begin{array}{c}{\mathbf{J}}_E\\ {\mathbf{J}}_j\end{array}\right]}^{†}\left(\begin{array}{c}{\mathbf{w}}_E^{\ast }\\ {\mathbf{w}}_j^{\ast }\end{array}\right)$$

我们同样可以直接计算组合后的雅克比矩阵的伪逆：

$$\begin{array}{rl}{\dot{\mathbf{q}}}_t^{\text{stack }}& ={\left[\begin{array}{c}{\mathbf{J}}_{E,t}\\ {\mathbf{J}}_{j,t}\end{array}\right]}^{†}\left(\begin{array}{l}{\mathbf{w}}_E^{\ast }\\ {\mathbf{w}}_j^{\ast }\end{array}\right)\\ & =\left(\begin{array}{c}-0.133\\ -0.067\\ -1.132\end{array}\right)\end{array}$$

于是我们会注意到：

$$\left[\begin{array}{c}{\mathbf{J}}_{E,t}\\ {\mathbf{J}}_{j,t}\end{array}\right]{\dot{\mathbf{q}}}_t^{\text{stack }}=\left(\begin{array}{c}1.039\\ 0.933\\ -0.133\\ -0.067\end{array}\right)\ne \left(\begin{array}{c}{\mathbf{w}}_E^{\ast }\\ {\mathbf{w}}_{\Delta \dot{q}}^{\ast }\end{array}\right)$$

我们可以看到：

$$\begin{array}{rl}{\Vert {\mathbf{w}}_{E,t}^{\ast }-{\mathbf{J}}_{E,t}{\dot{\mathbf{q}}}_t^{\text{stack }}\Vert }^2& =0.0059\\ {\Vert {\mathbf{w}}_{j,t}^{\ast }-{\mathbf{J}}_{j,t}{\dot{\mathbf{q}}}_t^{\text{stack }}\Vert }^2& =\mathrm{0.0223.}\end{array}$$
我们可以和前面的单任务进行对比：
$$\begin{array}{rl}{\Vert {\mathbf{w}}_{E,t}^{\ast }-{\mathbf{J}}_{E,t}{\dot{\mathbf{q}}}_t^{\text{single }}\Vert }^2& =0\\ {\Vert {\mathbf{w}}_{j,t}^{\ast }-{\mathbf{J}}_{j,t}{\dot{\mathbf{q}}}_t^{\text{single }}\Vert }^2& =0.319\end{array}$$
我们可以看到为了能实现第二个任务，我们牺牲了末端的跟踪性能。

3.3 多任务（存在优先级）

如果我们向保证末端的速度任务臂保证前面两个关节速度为0有更高的优先级，应该怎么做呢？

解答：
我们使用前面的公式：

$${\dot{\mathbf{q}}}_t^{\text{prio }}={\mathbf{J}}_1^{+}{\mathbf{w}}_1^{\ast }+{\mathbf{N}}_1{\left({\mathbf{J}}_2{\mathbf{N}}_1\right)}^{+}\left({\mathbf{w}}_2^{\ast }-{\mathbf{J}}_2{\mathbf{J}}_1^{+}{\mathbf{w}}_1^{\ast }\right)$$

这里：

$$\begin{gathered} {\mathbf{J}}_1={\mathbf{J}}_{E,t}=\frac{1}{2}\left[\begin{array}{ccc}0& -\sqrt{3}& -\sqrt{3}\\ -4& -3& -1\end{array}\right], \\ {\mathbf{J}}_2={\mathbf{J}}_{j,t}=\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\end{array}\right], \\ {\mathbf{w}}_1^{\ast }={\mathbf{w}}_{E,t}^{\ast }=\left(\begin{array}{l}1\\ 1\end{array}\right) \\ {\mathbf{w}}_2={\mathbf{w}}_{j,t}^{\ast }=\left(\begin{array}{l}0\\ 0\end{array}\right) \end{gathered}$$

我们可以计算一个可能的零空间的矩阵： $${\mathbf{N}}_1=\mathbb{I}-{\mathbf{J}}_1^{+}{\mathbf{J}}_1=\frac{1}{9}\left[\begin{array}{ccc}1& -2& 2\\ -2& 4& -4\\ 2& -4& 4\end{array}\right]$$

于是我们可以计算得到：

$${\dot{\mathbf{q}}}_t^{\text{prio }}=\left(\begin{array}{c}-0.169\\ -0.085\\ -1.070\end{array}\right)$$

现在我们再来看一下误差：

$$\begin{array}{rl}{\Vert {\mathbf{w}}_{E,t}^{\ast }-{\mathbf{J}}_{E,t}{\dot{\mathbf{q}}}_t^{\text{prio }}\Vert }^2& =0\\ {\Vert {\mathbf{w}}_{j,t}^{\ast }-{\mathbf{J}}_{j,t}{\dot{\mathbf{q}}}_t^{\text{prio }}\Vert }^2& =0.036\end{array}$$
与前面的优先级同等的解决方案相比，存在优先级的解总误差更大，但末端执行器任务的位置是准确的。与单个任务优化相比，可以看出总误差减少了。事实上，这是在不改变末端执行器跟踪性能的情况下降低关节速度，在最佳意义上使用了单维度零空间。

参考：

[1] Robot Dynamics Lecture Notes 43-47