背景描述
啦啦啦啦,然后拉拉阿里,然后啦啦啦,最后就写了这个记录一下
数据准备
1 管线数据
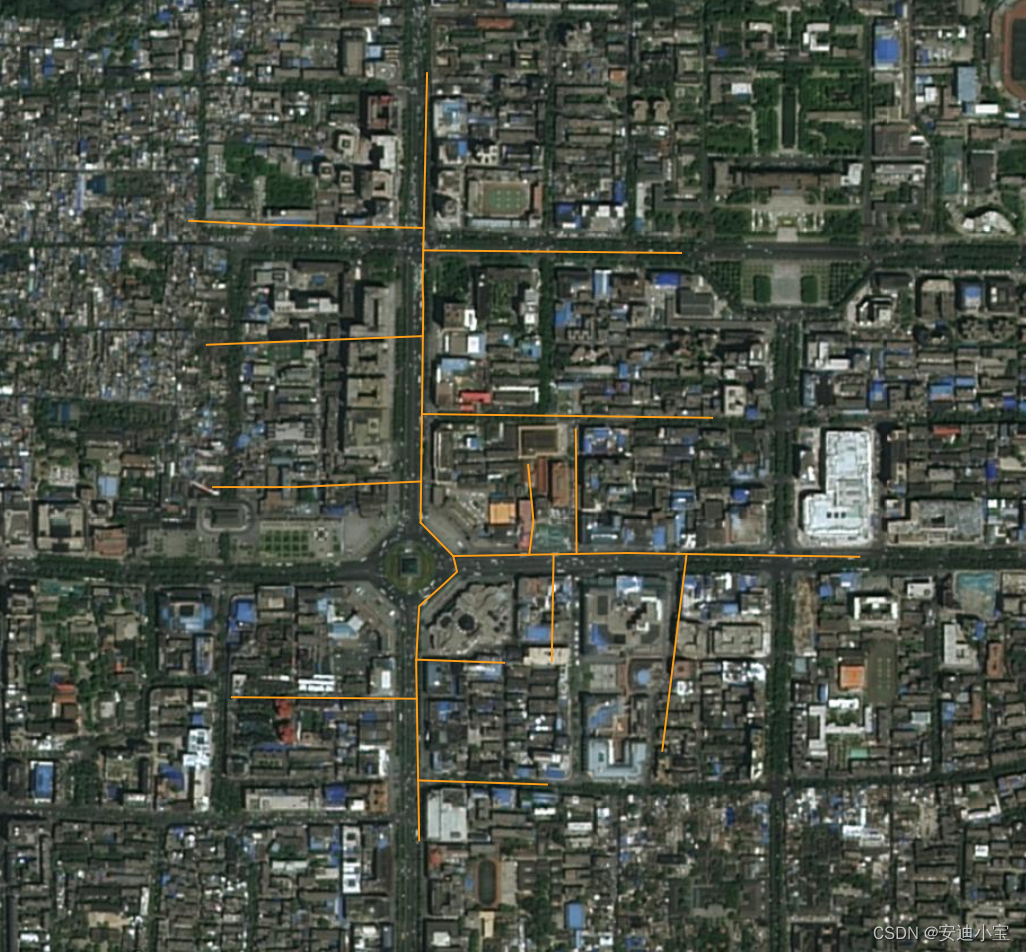
数据要求(拓扑检查)
-
数据没有重叠要求
-
数据悬挂点问题得到合理结局,不存在数据连接点不一样的线
-
数据能按照正常方向处理(如果没有流向等方向,数据将按照要素的绘制方向进行)
-
数据能够有通和不通的标识
导入到postgis中
| id | geom | shape_leng |
|---|---|---|
| 0 | 0105000020110F000001000000010200000002000000CE19510898216741808CB98B6D004F412C431C4D9821674190D409202E004F41 | 126.8595169 |
| 1 | 0105000020110F000001000000010200000002000000CE19510898216741808CB98B6D004F41B8D1001CBA21674130CB103769004F41 | 272.7527582 |
| 2 | 0105000020110F0000010000000102000000020000006C9A77AA9721674120C9E50FC4004F41CE19510898216741808CB98B6D004F41 | 173.0574528 |
| 3 | 0105000020110F0000010000000102000000020000006C9A77AA9721674120C9E50FC4004F41E61DA7BA66216741E07A149EC5004F41 | 391.506559 |
| 4 | 0105000020110F000001000000010200000003000000EC9E3C8E97216741B0D85F6EED004F414E62108297216741801D384FE9004F416C9A77AA9721674120C9E50FC4004F41 | 82.75757135 |
| 5 | 0105000020110F000001000000010200000002000000EC9E3C8E97216741B0D85F6EED004F41744694CEAE21674160FE431AEA004F41 | 186.1297867 |
| 6 | 0105000020110F000001000000010200000006000000143FC652A1216741701283205B014F412A189550A2216741701283784A014F41C0CAA1F19E216741A0BDC1C73D014F412C431C4D98216741D0D556FC25014F41C66D34CE97216741F05A421603014F41EC9E3C8E97216741B0D85F6EED004F41 | 255.8795071 |
| 7 | 0105000020110F000001000000010200000002000000143FC652A1216741701283205B014F4182734670B5216741E0F21F825C014F41 | 160.9456115 |
| 8 | 0105000020110F00000100000001020000000200000082734670B5216741E0F21F825C014F41B0506BE2BB216741907571F35C014F41 | 51.57459883 |
| 9 | 0105000020110F000001000000010200000002000000B0506BE2BB216741907571F35C014F41FC87F465BB21674120C05BB0EB004F41 | 226.5574896 |
| 10 | 0105000020110F000001000000010200000002000000C286A717DF216741F097DD3B5D014F41182653A5D8216741C06D34E88C004F41 | 419.8332718 |
| 11 | 0105000020110F000001000000010200000003000000C286A717DF216741F097DD3B5D014F414E401313F8216741705F07865B014F41A089B0CB0C226741903177555A014F41 | 365.6724458 |
| 12 | 0105000020110F000001000000010200000002000000B0506BE2BB216741907571F35C014F41EE7C3FF1C12167419028ED5D5D014F41 | 48.47053948 |
| 13 | 0105000020110F000001000000010200000003000000EE7C3FF1C12167419028ED5D5D014F41F0164886CF216741F095B24C5E014F41C286A717DF216741F097DD3B5D014F41 | 233.2344497 |
| 14 | 0105000020110F000001000000010200000002000000F4FDD4AE982167412063EE827E014F41143FC652A1216741701283205B014F41 | 98.92549714 |
| 15 | 0105000020110F000001000000010200000003000000F085C9D09821674120FDF60DAA014F418295434977216741B08BDB18A4014F41083D9BC561216741B08BDB18A4014F41 | 440.6138972 |
| 16 | 0105000020110F000001000000010200000002000000F4FDD4AE982167412063EE827E014F41F085C9D09821674120FDF60DAA014F41 | 87.09266423 |
| 17 | 0105000020110F00000100000001020000000300000082734670B5216741E0F21F825C014F41168C4A8AB6216741D0C342CD80014F41D8F0F426B52167418026C27EBB014F41 | 191.0307803 |
| 18 | 0105000020110F000001000000010200000003000000EE7C3FF1C12167419028ED5D5D014F415817B7D7C1216741305530A2C2014F41623255BEC1216741E0D7812BE1014F41 | 263.6128224 |
| 19 | 0105000020110F000001000000010200000002000000F085C9D09821674120FDF60DAA014F41D881730899216741A0DFBE6EF1014F41 | 142.7666976 |
| 20 | 0105000020110F000001000000010200000002000000D881730899216741A0DFBE6EF1014F410022FDD4E5216741A0DFBE76ED014F41 | 614.4430713 |
| 21 | 0105000020110F0000010000000102000000020000003AB4C8489921674170787AED43024F4152962116602167412051DACB3A024F41 | 457.9471985 |
| 22 | 0105000020110F000001000000010200000002000000D881730899216741A0DFBE6EF1014F413AB4C8489921674170787AED43024F41 | 165.0023479 |
| 23 | 0105000020110F0000010000000102000000040000003AB4C8489921674170787AED43024F413A014D649921674120E4833667024F4102098A3199216741A0B437707B024F41141DC96199216741803F35BE9E024F41 | 181.6831255 |
| 24 | 0105000020110F000001000000010200000002000000141DC96199216741803F35BE9E024F41F6065F9ADD216741E08C28F59B024F41 | 545.7967295 |
| 25 | 0105000020110F000001000000010200000002000000141DC96199216741803F35BE9E024F41CAE53F829921674140795880B6024F41 | 47.52752875 |
| 26 | 0105000020110F000001000000010200000003000000CAE53F829921674140795880B6024F41907EFB5C6E21674190C2F518BA024F41ECC0396D5B216741F0263110BE024F41 | 496.9394137 |
| 27 | 0105000020110F000001000000010200000002000000CAE53F829921674140795880B6024F4152DA1B629A216741505986505A034F41 | 327.7010778 |
分析
建立管线拓扑关系
建立拓扑关系主要目的是为了确定管线每一段的源头和终点,简单说就是两个阀之间关系。数据库中入库数据确定管线的上游阀source和下游阀target,cost用于计算连通,cost>0表示上游到下游可联通,cost<0表示不通
reverse_cost也是用于标识连通性,reverse_cost>0标识下游到上游是联通的,reverse_cost<0标识不通
ALTER TABLE testpipeline ADD COLUMN "source" INTEGER default null;
ALTER TABLE testpipeline ADD COLUMN "target" INTEGER default null;
ALTER TABLE testpipeline ADD COLUMN "cost" DOUBLE PRECISION default null;
注意:如果数据量大,可以通过创建索引提高查询效率,分别穿件source和target的索引
赋值
这里使用管线长度来做为联通性标识,即从source到target都是联通的
UPDATE testpipeline SET cost =st_length(geom);
如果是供水等管线,可以更具实际情况对source、target、cost,reverse_cost赋值
拓扑创建
创建拓扑是给线生成点文件
原理是提取线段的起点和结束点,作为管线(testpipeline)的source和target。按照折线的绘制方向生成。
生成一个新的点表,存储有id,和空间信息
select pgr_createtopology('testpipeline',0.0001,the_geom:='geom',id:='id',source:='source',target:='target',rows_where:='true', clean:=false)
- edge_table:text,表名’testpipeline’
- tolerance:float8,误差缓冲值,两个点的距离在这个距离内,就算重合为一点。0.0001
- the_geom:text,该表的空间坐标字段’geom’
- id:text,该表的主键 ‘id’
- source:text,空间起点编号’source’
- target:text,空间终点编号’target’
- rows_where:text,条件选择子集或行。默认值为true,表示源或目标具有空值的所有行,否则将使用条件。‘true’
- clean:text,每次执行都重建拓扑图,默认false false
| id | cnt | chk | ein | eout | the_geom |
|---|---|---|---|---|---|
| 1 | 0101000020110F0000CE19510898216741808CB98B6D004F41 | ||||
| 2 | 0101000020110F00002C431C4D9821674190D409202E004F41 | ||||
| 3 | 0101000020110F0000B8D1001CBA21674130CB103769004F41 | ||||
| 4 | 0101000020110F00006C9A77AA9721674120C9E50FC4004F41 | ||||
| 5 | 0101000020110F0000E61DA7BA66216741E07A149EC5004F41 | ||||
| 6 | 0101000020110F0000EC9E3C8E97216741B0D85F6EED004F41 | ||||
| 7 | 0101000020110F0000744694CEAE21674160FE431AEA004F41 | ||||
| 8 | 0101000020110F0000143FC652A1216741701283205B014F41 | ||||
| 9 | 0101000020110F000082734670B5216741E0F21F825C014F41 | ||||
| 10 | 0101000020110F0000B0506BE2BB216741907571F35C014F41 | ||||
| 11 | 0101000020110F0000FC87F465BB21674120C05BB0EB004F41 | ||||
| 12 | 0101000020110F0000C286A717DF216741F097DD3B5D014F41 | ||||
| 13 | 0101000020110F0000182653A5D8216741C06D34E88C004F41 | ||||
| 14 | 0101000020110F0000A089B0CB0C226741903177555A014F41 | ||||
| 15 | 0101000020110F0000EE7C3FF1C12167419028ED5D5D014F41 | ||||
| 16 | 0101000020110F0000F4FDD4AE982167412063EE827E014F41 | ||||
| 17 | 0101000020110F0000F085C9D09821674120FDF60DAA014F41 | ||||
| 18 | 0101000020110F0000083D9BC561216741B08BDB18A4014F41 | ||||
| 19 | 0101000020110F0000D8F0F426B52167418026C27EBB014F41 | ||||
| 20 | 0101000020110F0000623255BEC1216741E0D7812BE1014F41 | ||||
| 21 | 0101000020110F0000D881730899216741A0DFBE6EF1014F41 | ||||
| 22 | 0101000020110F00000022FDD4E5216741A0DFBE76ED014F41 | ||||
| 23 | 0101000020110F00003AB4C8489921674170787AED43024F41 | ||||
| 24 | 0101000020110F000052962116602167412051DACB3A024F41 | ||||
| 25 | 0101000020110F0000141DC96199216741803F35BE9E024F41 | ||||
| 26 | 0101000020110F0000F6065F9ADD216741E08C28F59B024F41 | ||||
| 27 | 0101000020110F0000CAE53F829921674140795880B6024F41 | ||||
| 28 | 0101000020110F0000ECC0396D5B216741F0263110BE024F41 | ||||
| 29 | 0101000020110F000052DA1B629A216741505986505A034F41 |
字段介绍
| id: | bigint 顶点的标识符。 |
|---|---|
| cnt: | integer edge_table中引用此顶点的顶点数。See pgr_analyzeGraph. |
| chk: | integer 指示顶点可能有问题。See pgr_analyzeGraph. |
| ein: | integer edge_table中引用这个顶点的顶点数。See pgr_analyzeOneway. |
| eout: | integer edge_table中引用该顶点作为输出的顶点数。See pgr_analyzeOneway. |
| the_geom: | geometry Point geometry of the vertex:顶点的点几何。 |
查找联通性
此处联通性计算使用Dijkstra算法,其原理是找出两点的最短路径,如果能找到最短路径说明是联通的,并放回最短路径,如果找不到,说明不连通。
Dijkstra算法,由荷兰计算机科学家Edsger Dijkstra(上面的照片就是这位大佬!)于1956年提出。它是一种图搜索算法,它解决了非负代价边路径图的最短路径问题,即从起始顶点(start_vid)到结束顶点(end_vid)的最短路径。此算法可以与有向图或无向图一起使用。
select * from pgr_dijkstra('select id ,source,target,cost::double precision from testpipeline',28,14,directed:=false)
- edges sql Text,要进行分析的表及相关字段
- strart_vids 起点id
- end_vids 终点id
- directed参数的值,默认true,true计算过程考虑图的方向,false计算过程不考虑图的方向
查询结果
| seq | path_sql | node | edge | cost | agg_cost |
|---|---|---|---|---|---|
| 1 | 1 | 28 | 26 | 496.9394137 | 0 |
| 2 | 2 | 27 | 25 | 47.52752875 | 496.9394137 |
| 3 | 3 | 25 | 23 | 181.6831255 | 544.4669425 |
| 4 | 4 | 23 | 22 | 165.0023479 | 726.150068 |
| 5 | 5 | 21 | 19 | 142.7666976 | 891.1524158 |
| 6 | 6 | 17 | 16 | 87.09266423 | 1033.919113 |
| 7 | 7 | 16 | 14 | 98.92549714 | 1121.011778 |
| 8 | 8 | 8 | 7 | 160.9456115 | 1219.937275 |
| 9 | 9 | 9 | 8 | 51.57459883 | 1380.882886 |
| 10 | 10 | 10 | 12 | 48.47053948 | 1432.457485 |
| 11 | 11 | 15 | 13 | 233.2344497 | 1480.928025 |
| 12 | 12 | 12 | 11 | 365.6724458 | 1714.162474 |
| 13 | 13 | 14 | -1 | 0 | 2079.83492 |
node节点顺序
edge 管线顺序







![Android性能优化篇[谷歌官方]](https://img-blog.csdnimg.cn/img_convert/b0054765d5f6cfa7e156028dd38b3f4a.jpeg)