前奏:
迪菲-赫尔曼密钥交换是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。
颜色混合:
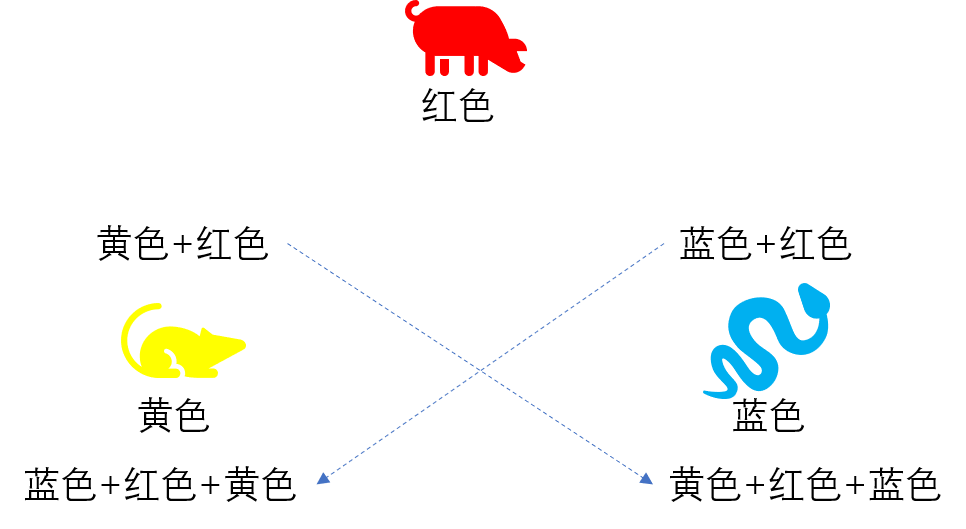
如图所示,蛇和老鼠要交换一个共享密钥,双方以猪的颜色红色为基准(公开的),老鼠用自己的黄色(私有)加上红色然后公开出去这一混合颜色,蛇用自己的蓝色(私有)加上红色然后公开这一混合颜色。
此时,蛇,老鼠,猪都能看到的公开颜色是红色,红色混合了黄色,蓝色混合了红色。老鼠获取了蛇的混合颜色蓝红,然后加入自己的黄色,得到了另一种混合颜色蓝红黄,同理,蛇获取了老鼠公开的颜色黄红,然后加入了自己的蓝色,得到了混合颜色黄红蓝。
蛇鼠一窝最终获取了相同的混合颜色,而猪却无法得知最终的混合颜色。因为颜色有色差,猪无法从老鼠的混合颜色黄红中推测出老鼠用的是黄色,只能采取暴力破解(可能需要N年)。
数字相乘:
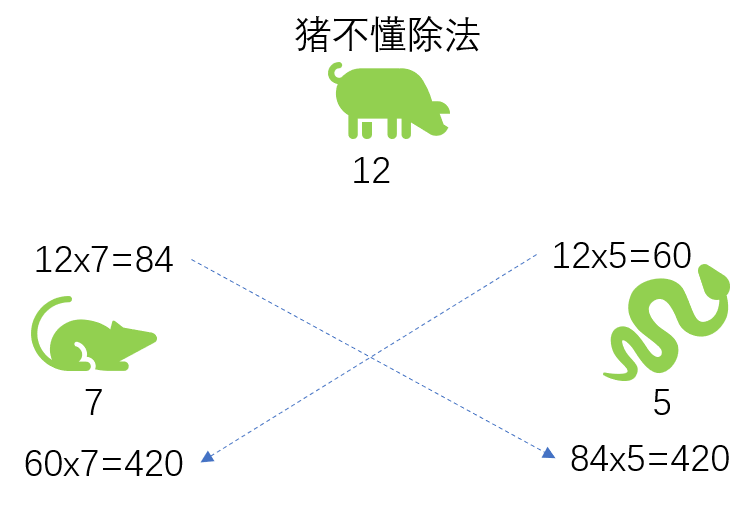
如图所示,蛇和老鼠再次传递共享密钥,不玩颜色把戏了,这回玩数字游戏。公开数字12,老鼠用自己的私有数字7乘以12,然后将结果84公开出去,蛇用自己的私有数字5乘以12,然后将结果60公开出去。
此时,蛇,老鼠,猪都能看到的数字是12,84,60。老鼠获取了蛇的公开数字60,然后乘以私有数字7得到结果420。同理,蛇获取老鼠公开的数字84,然后乘以私有数字5得到结果420。
蛇鼠一窝最终获取了相同的数字420,而猪却无法从三个公开的数字得到最终的数字,这里假设猪不会除法,只能使用乘法暴力破解。这里只是使用简单的乘法运算,下面会升级。
钟算和幂:
钟表上有12个数字,从1到12,过了12又重新回到1,所以13点就是1点(13-1=12),20点就是8点(20-12=8)。钟的大小可以任意设置,通常从0开始。比如钟大小为11代表从0到10,钟算(20)=9。
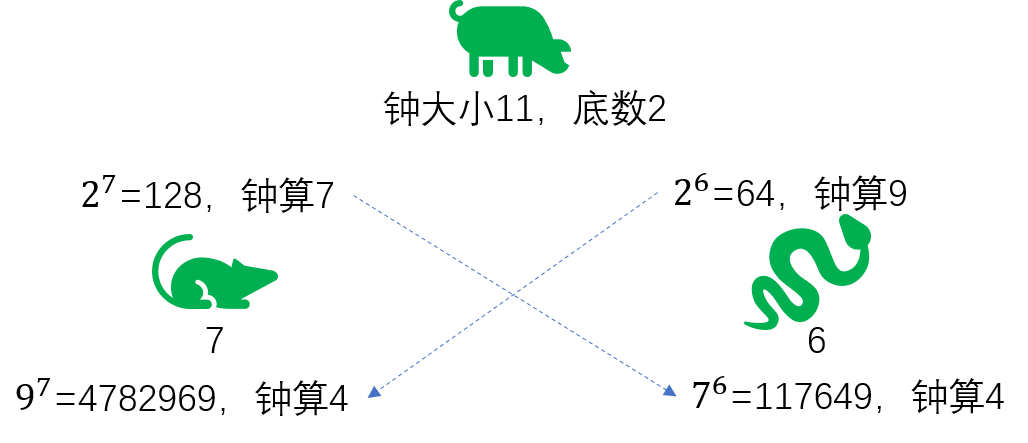
如图所示,蛇和老鼠再次传递共享密钥,钟大小公开选择11,底数公开选择2,老鼠根据底数2,用自己的私人数字7对底数进行幂运算,得到的结果进行钟算,钟算结果7公开。同理蛇根据底数2,用自己的私人数字6对底数进行幂运算,得到的结果进行钟算,钟算结果9公开。
此时,蛇,老鼠,猪都能知道钟大小11,底数2,公开的数字9和7。老鼠获取了蛇的公开数字9,然后使用自己的私有数字对9求幂,结果进行钟算最终得到结果4。同理蛇获取老鼠的公开数字7,然后使用自己的私有数字6对7求幂,结果进行钟算最终得到结果4。
蛇鼠一窝最终获取了相同的数字4,即便猪知道钟大小和底数,但无法得知7和9是由哪个数字钟算而来的。这里的数字还比较小,倘若取非常大的数字,暴力求解都有心无力。
知识补充:
1、钟大小的选择必须是素数,且底数必须为钟大小的本原根。
2、本原根:对底数求幂进行钟算,结果将会循环遍1~(钟大小-1)。
3、互质,两个数字的公约数只有1。
4、欧拉函数,小于n的正整数中与n互质的数字的个数。



![Android性能优化篇[谷歌官方]](https://img-blog.csdnimg.cn/img_convert/b0054765d5f6cfa7e156028dd38b3f4a.jpeg)