title: 前缀、中缀、后缀表达式及简易运算实现总结
date: 2023-06-30 10:25:50
tags:
- 表达式
categories: - 开发知识及其他
cover: https://cover.png
feature: false
1. 概念
1.1 什么是前缀、中缀、后缀表达式?
- 前缀表达式:又称波兰式(Polish Notation),操作符以前缀形式位于两个运算数前(如:3 + 2 的前缀表达形式就是 + 3 2)
- 中缀表达式:操作符以中缀形式位于运算数中间(如:3 + 2),是我们日常通用的算术和逻辑公式表示方法
- 后缀表达式:又称逆波兰式(Reverse Polish Notation - RPN),操作符以后缀形式位于两个运算数后(如:3 + 2 的后缀表达形式就是 3 2 +)
中缀表达式往往需要使用括号将操作符和对应的操作数括起来,用于指示运算的次序,如 5 * (2 + 1) 虽然 * 的优先级高于 + ,但括号的存在表示应优先执行括号内的 + 运算。适合于人类的思维结构和运算习惯,但并不适用于计算机
与中缀表达式不同,前缀和后缀表达式都不需要使用括号来标识操作符的优先级,适用于计算机。不过后缀表达式的计算按操作符从左到右出现的顺序依次执行(不考虑运算符之间的优先级),更加符合人类的阅读习惯,因此实际计算机程序中,基本都是用后缀表达式来存储公式的,前缀表达式效果次之。对于中缀表达式,我们则可以先将其转为后缀表达式,再进行求值
1.2 树结构对应
其实前缀表达式、中缀表达式、后缀表达式就是通过树来存储和计算表达式的三种不同方式,分别对应树的先序遍历、中序遍历、后序遍历。如下图,这是一颗二叉树
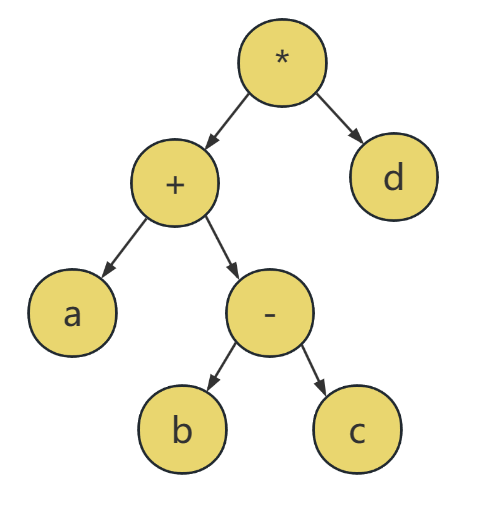
- 上面的树,先序遍历就是 *+a−bcd,即对应前缀表达式
- 中序遍历是 a+b−c∗d,但是这样的表示是有歧义的,这样表示 ab 是一颗子树,cd 是一颗子树,然后相减,所以中缀表达式必须借助括号,才能正确地表达出想要的结果。中缀表达式为:(a+(b−c))∗d,括号表示一个子树的整体
- 后序遍历是 abc−+d∗,即对应的后缀表达式
2. 表达式求值
2.1 通过树结构存储和求值表达式
实现思路比较简单,如果节点上存的是参数,那么该参数的值,就是该节点的值;如果节点上存的操作符,拿该节点左子树和右子树做对应运算,得到的结果作为该节点的值
代码略
2.2 前缀表达式解析和求值
∗ + a − b c d ∗+a−bcd ∗+a−bcd
观察前缀表达式的规律可以发现,每当连续出现两个数值时,前面必定会有一个操作符,这是先序遍历的特征决定的(根左右,根即为表达式),因此我们依次取三个元素出来,判断符合连续两个数值条件的进行运算,就可以得到一个操作符节点的数值,如此反复递归,最终就能求出表达式的值
代码略
2.3 后缀表达式解析和求值
a b c − + d ∗ abc−+d∗ abc−+d∗
和前缀表达式类似,其实也就是后序遍历的特征,即只要有运算符出现的地方,前面两个元素一定是操作数(左右根),然后同样取三个元素出来,判断符合条件的进行运算
详细代码见 3
2.4 中缀表达式转后缀表达式
( a + ( b − c ) ) ∗ d (a+(b−c))∗d (a+(b−c))∗d
中缀表达式直接求值比较麻烦,所以我们将其转换为后缀表达式,再求值就方便了。中缀表达式转后缀表达式的难点在于,要考虑括号和运算符优先级,步骤如下,这个转换算法不是凭空产生的,而是根据后缀表达式的特点反推出来的
- 创建两个栈,S1 用来存输出元素,S2 用来存运算符。由于表达式中的运算符是有优先级的,所以必须通过栈来暂存起来
- 从中缀表达式栈顶开始,向栈尾逐个读取元素
- 如果读到操作数,直接加到 S1 栈尾。因为后缀表达式操作数永远是在运算符前面的
- 如果读到左括号,则直接压入 S2 栈顶。因为左括号要等到右括号时才能处理
- 如果读到运算符,且 S2 栈为空或 S2 栈顶元素为左括号,则直接压入 S2 栈顶。因为这种情况不需要比较运算符优先级
- 如果读到运算符,且 S2 栈顶也为运算符,且当前运算符优先级大于栈顶元素,则将当前运算符压入 S2 栈顶。因为后面读取到的运算符可能比当前运算符优先级更高,因此暂时不能输出当前运算符
- 如果读到运算符,且 S2 栈顶也为运算符,且当前运算符优先级小于等于栈顶元素,则将 S2 栈顶运算符弹出,加到 S1 栈尾。因为优先级高的运算符要先参加运算。注意,这是一个递归过程,因为 S2 中可能已存在多个运算符,它们的优先级可能都大于等于当前运算符,当这些运算符都弹出时,再将当前运算符压入 S2 栈顶
- 如果读到右括号,则将 S2 内首个左括号以上的运算符,全部加到 S1 栈尾。因为括号的优先级是最高的,立刻进行运算
例:中缀表达式 2*(3+5)+7/1-4 转换为后缀表达式
可以先转换为树,然后后序遍历得到后缀表达式,再和通过上面步骤推算出来的结果进行验证,判断是否正确。转换需要强调的是,我们用括号表示优先计算
表达式 2*(3+5)+7/1-4 中我们约定 * 和 / 的优先级高于 + 和 -,因此 + 和 - 要优先计算时需要加上括号。但是本身对于 + 和 - 来说,* 和 / 优先级高也是一种优先计算,优先计算就需要加上括号,只是我们一开始约定了先算 * 和 /,同时也为了方便,因此省略了括号
包括同级的 * 和 / 或 + 和 -,我们约定了从左往右算,其实先算左边的,也是一种优先计算,我们给优先计算的都加上括号,那么原式应为:((2*(3+5))+(7/1)) -4
强调这一点主要为了转换成树的时候方便划分左右子树,括号为一个子树的整体,这样一来转换成树的结构就很清晰了,[左子树 运算符 右子树]

后序遍历为:235+*71/+4-,即后缀表达式
此时再通过上面的步骤得到后缀表达式
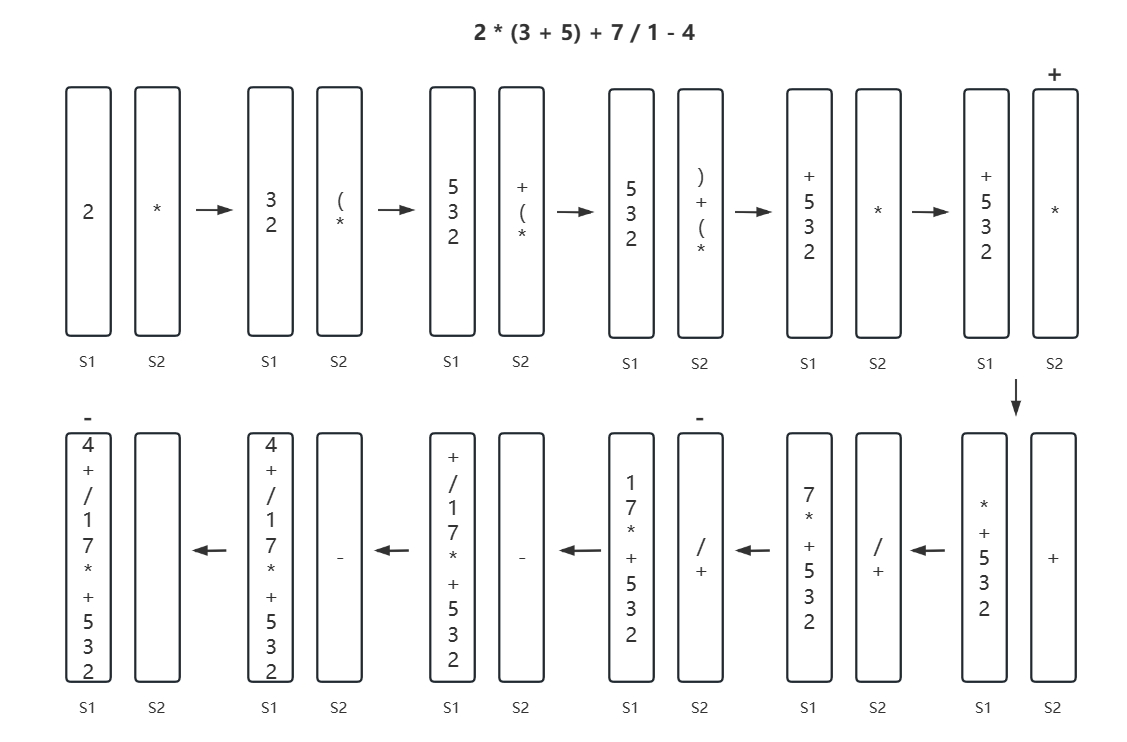
可以看到最终结果也是 235+*71/+4-
详细代码见 3
3. 简易运算实现
Calculator 类
public class Calculator {
private static final Map<String, Integer> OPERATORS = MapUtil.builder("+", 1).put("-", 1).put("*", 2).put("/", 2)
.put("%", 2).put("^", 3).put("(", 0).put(")", 0).build();
private Calculator() {
}
public static double calculate(String equation) {
if (!BaseUtil.isWholeSymbol(equation)) {
throw new IllegalArgumentException("请确认括号是否完整");
}
Deque<String> operand = new ArrayDeque<>();
Deque<String> operator = new ArrayDeque<>();
for (String str : toList(equation)) {
if (NumberUtils.isCreatable(str)) {
operand.push(str);
continue;
}
Integer opt = OPERATORS.get(str);
if (null == opt) {
throw new IllegalArgumentException("操作符不合法");
}
if (StrPool.LBRACKET.value().equals(str) || operator.isEmpty() || opt > OPERATORS.get(operator.peek())) {
operator.push(str);
} else if (StrPool.RBRACKET.value().equals(str)) {
// 判断是否是右括号, 存在右括号则运算符栈必有左括号, 即运算符栈不为空
while (!operator.isEmpty()) {
if (StrPool.LBRACKET.value().equals(operator.peek())) {
operator.pop();
break;
} else {
String calculate = calculate(operator.pop(), operand.pop(), operand.pop());
operand.push(calculate);
}
}
} else if (opt <= OPERATORS.get(operator.peek())) {
while (!operator.isEmpty() && opt <= OPERATORS.get(operator.peek())) {
String calculate = calculate(operator.pop(), operand.pop(), operand.pop());
operand.push(calculate);
}
operator.push(str);
}
}
while (!operator.isEmpty()) {
String calculate = calculate(operator.pop(), operand.pop(), operand.pop());
operand.push(calculate);
}
return Double.parseDouble(operand.pop());
}
public static List<String> toList(String str) {
List<String> list = new ArrayList<>();
StringBuilder builder = new StringBuilder();
String replace = str.replaceAll("\\s*", "");
char[] chars = replace.toCharArray();
for (int i = 0; i < chars.length; i++) {
boolean isMinus = '-' == chars[i] && (i == 0 || '(' == chars[i - 1]);
if (isMinus) {
builder.append(chars[i]);
continue;
}
String val = String.valueOf(chars[i]);
if (null != OPERATORS.get(val)) {
if (StringUtil.INSTANCE.isNotBlank(builder)) {
list.add(builder.toString());
}
list.add(val);
builder = new StringBuilder();
} else {
builder.append(chars[i]);
}
}
if (StringUtil.INSTANCE.isNotBlank(builder)) {
list.add(builder.toString());
}
return list;
}
private static String calculate(String operator, String val2, String val1) {
double pre = Double.parseDouble(val1);
double suf = Double.parseDouble(val2);
switch (operator) {
case "+":
return pre + suf + "";
case "-":
return pre - suf + "";
case "*":
return pre * suf + "";
case "/":
return pre / suf + "";
case "%":
return pre % suf + "";
case "^":
return Math.pow(pre, suf) + "";
default:
return "0";
}
}
}
BaseUtil 类
public class BaseUtil {
private static final Map<Character, Character> R_SYMBOL = MapUtil.builder(')', '(').put(']', '[').put('}', '{').build();
private static final List<Character> L_SYMBOL = ListUtil.list('(', '[', '{');
private BaseUtil() {
}
public static boolean isWholeSymbol(String str) {
Deque<Character> symbol = new ArrayDeque<>();
for (char ch : str.toCharArray()) {
if (R_SYMBOL.containsKey(ch)) {
if (symbol.isEmpty() || !symbol.peek().equals(R_SYMBOL.get(ch))) {
return false;
}
symbol.pop();
} else if (L_SYMBOL.contains(ch)) {
symbol.push(ch);
}
}
return symbol.isEmpty();
}
}