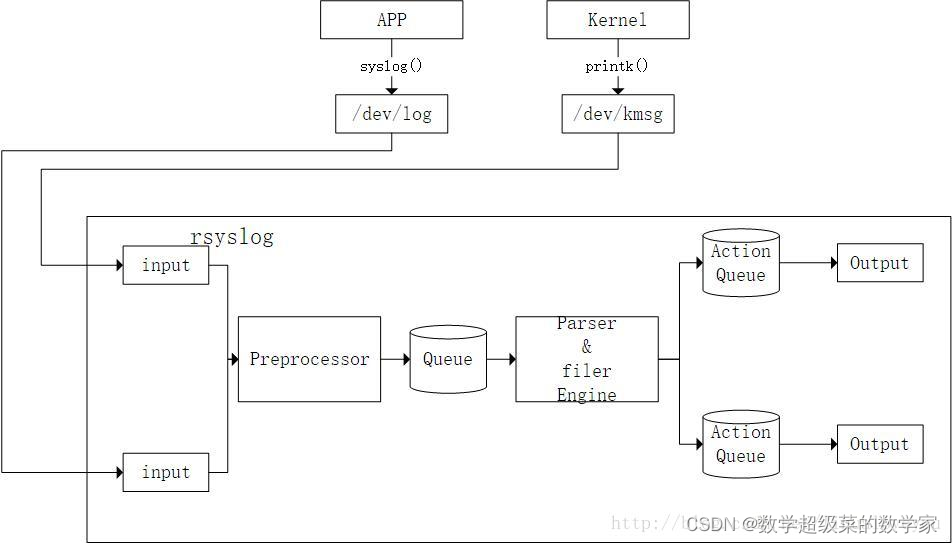
这是面积的推广，这里引出了格拉姆矩阵，有了这个，我们得到的矩阵总是方阵，可以绕过雅可比矩阵不存在的问题。能得到通用的积分换元公式。

 

其实任何时候，从几何意义去理解总是更加自然。考虑一个平面上的坐标，我们任意一个坐标基方向的极小的变化，都会引起曲面上的一个极小的变化。这个极小的变化的向量，是两个点的差值，根据微分中值定理，我们可以找到这点的导数对应的自变量变化的乘积。这样就很自然的引入了雅可比矩阵。

 

 非常快速的推导出了弧长微分公式和曲面参数方程求面积的方法。相比起之前的做法，确实可以感受到什么会当凌绝顶，一览众山小。

 

 后面是说可以去掉k-1维的部分，但积分的结果是不变的。这个好处是很多图册需要2张，但我们如果去掉其中一张，积分不变，那么就很好进行积分计算。

微分形式的引入是比较奇怪的，参考：流形上的微分形式有何深层次意义？ - 知乎 

按照这样的理解，我们继续看教材。

 

 

外积的良好性质。

 

 首先L是1形式，也就是曲线映射到一个具体的值。通过外积操作，可以升维，具体的数值是通过矩阵的行列式来对应的。暂时还看不出这个矩阵具体和积分有什么关系。继续看。

这是一个常见的映射，得到的矩阵就是每个向量本身，那么行列式的值其实也就是围成的体积。

这是k形式，也就是是一个k维曲面映射到一个常数。而这个常数是一个矩阵的行列式，矩阵的每一个元素对应着k个向量的k个坐标。

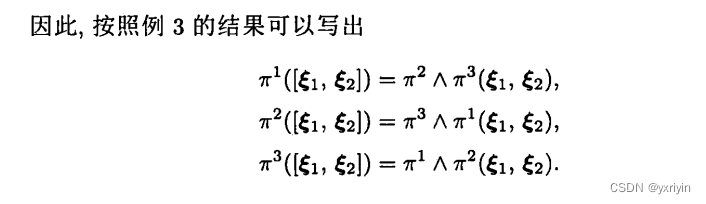 等号

我们先不管，但我们可以看到，左边是1形式，外积是一个线，右边是二形式，是一个面。

 

 这里是把L用微分来代替了，这样其实就是雅可比矩阵了。

 这里说的是切空间到实数的映射是一个反对称形式。

 这里引出了功形式，其实就是做功。他是内积，但也可以从前面的微分来看待这个。向量场F的梯度gradf也是一个向量，对于任何切空间中的向量，gradf作用于它就相当于求导。这个其实就是1形式。这样想的话也就不用考虑内积了。

 这里字很多，但其实就是流形式，考虑三维下的一个曲面，然后水流流过这个曲面。那么最终这个流量也是个实数。这就是2形式，把一个曲面映射到一个实数。

 微分形式的坐标：L是k形式。对于基向量，应该存在一个坐标。记下坐标和对应的L作用在基向量上的值就行。那个值是固定的，变化的只是坐标。

这是一个比较重要的例子，从里面我们可以看到因为每个坐标都是基坐标的求和，所以都需要展开，写成求和公式后，这个坐标形式看着还是挺复杂的。

 

 扩大到k维之后，更加复杂了。改成外积感觉还是很复杂啊。感觉坐标形式并不是一个很好的记忆点。

不过这个形式可以启发我们的思考，对于任何k维的形式，可以拆成一堆最简单k形式的组合，而这些组合的单个个体是一堆1形式的外积。

 

再次强调概念，微分作用在一个向量上，可以看成1形式。一个向量和求导的点积。

流形式更多的是看成流量，水流流过一个k-1维曲面的流量。因为V是可以控制的，所以就可以通过它来作为流量函数。不过具体的值应该还是旋度。不是流量。

这里还要记住，2形式作用在一个平面上。

 

 

要注意这个和前面1形式梯度的区别，那个是对向量求导，这个是对点求导。

 

因为每个k形式都可以是最简k形式的线性组合，所以这里的dx,dy就是最简的1形式。它作用在具体的向量上，就是取到对应的坐标吧。dx取x坐标，dy取y坐标。如果是2形式，那么就是用取到的坐标组成一个矩阵的行列式。

这是梯度旋度散度的概念。可以看到他们并没有包含1形式，2形式，3形式。也就是后面少了一个行列式的值。不过确实，行列式的值也是受到输入的控制的，真正函数本身还是这些物理量本身。

 

 从这里还可以看到，梯度的导数是旋度，旋度的导数是散度。