奇异值分解(SVD)

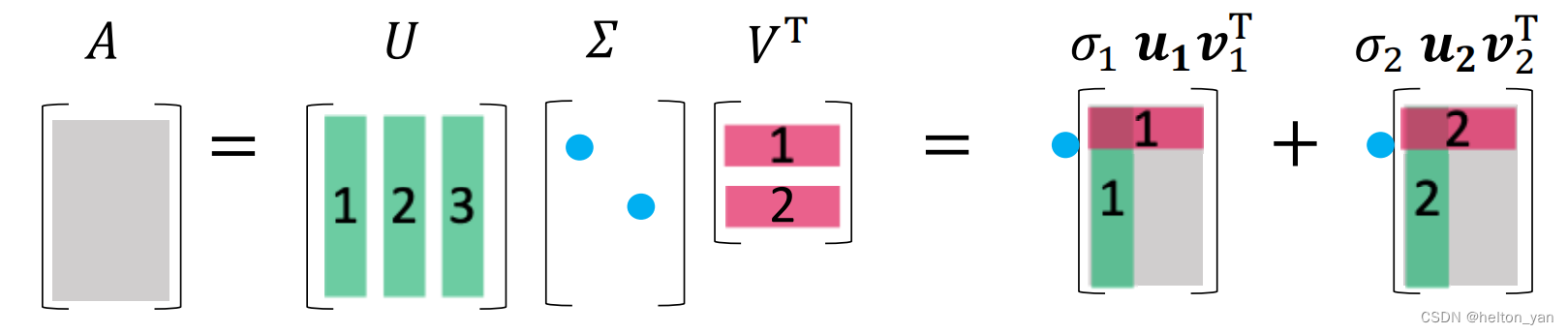
在这里插入图片描述

奇异值分解(Singular Value Decomposition) 是矩阵低秩分解的一种方法，在机器学习领域具有广泛的应用。它不光可以用于图像压缩，降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是许多机器学习算法的基石。
本篇博客中所有的可视化及数据预处理代码已上传至github：
Machine-Learning/SVD_PCA at main · Scienthusiasts/Machine-Learning (github.com)

1.理论部分

鉴于逻辑的连贯性，在搞清楚什么是奇异值分解之前，我们先来聊聊矩阵的特征分解。

1.1特征分解(ED)

我们知道，任何矩阵都有特征值和特征向量，它们的定义如下：
$\xi=\lambda \xi$
其中λ是A的特征值，ξ是A的特征向量。

现在我们假设A为n阶方阵，并且有n个特征值，对应n个线性无关的特征向量，我们求出A的n个特征值和特征向量，并将这n个特征值按从大到小的顺序排列，构成对角阵Λ，相应的，将n个特征向量构成一个可逆矩阵P，即：
$\Lambda=\left[\begin{array}{ccc} \lambda_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_n \end{array}\right], \mathrm{P}=\left[\xi_1 \cdots \xi_{\mathrm{n}}\right]$
则有：
$\mathrm{AP}=\mathrm{P} \Lambda \Rightarrow \mathrm{A}=\mathrm{P} \Lambda \mathrm{P}^{-1}$
进一步地，我们将A的n个特征向量标准正交化，即P是一个正交矩阵，则有：
$\mathrm{A}=\mathrm{P} \Lambda \mathrm{P}^{T}$
这样一来，我们便将一个方阵A分解成为了一个对角阵和一个正交阵，相信大家对此都非常的熟悉，因为这就是方阵的相似对角化，只不过研究的领域不同，叫法也有所差异。

值得一提的是，上面这种形式还可以写成：
$\mathrm{A}=\sum_{\mathrm{i}=1}^{\mathrm{n}} \lambda_{\mathrm{i}} \xi_{\mathrm{i}}^{\mathrm{T}} \xi_{\mathrm{i}}$
注意到ξᵀξ是一个秩为1的和A同样大小的矩阵，这就相当于：我们可以通过n个秩为1的方阵，通过加权(λᵢ)求和的方式，还原出原始矩阵A。

我们可以顺便从图像的角度来理解，假设图像的尺寸为nxn大小。图像的秩为为n，那么，我们就可以通过特征分解将图像分解为n个秩为1的子图像，通过对这n个子图像加权求和，不断升高图像的秩，我们就可以逐渐还原出原始图像。

(因为ξᵢ线性无关，所以每加一次，图像矩阵的秩+1)

到这里，虽然还没引出奇异值分解，我想各位也已经对奇异值分解有一个模糊的认知了，因为特征分解就是奇异值分解当A为方阵的特殊情况。换句话说，奇异值分解更进一步适用于非方阵矩阵的情况。

1.2 奇异值分解(SVD)

考虑到矩阵的特征分解有以下几个局限性：

1.矩阵必须是方阵

2.矩阵属于同一特征值的两个特征向量线性无关。

除此之外，考虑到实际中非方阵才是更普遍的情况，因此SVD相比ED是更为通用的矩阵分解方法，但其推导过程中依然会用到特征分解。

我们首先给出SVD分解的结论，再来进一步进行推导，这样会更容易理解。

SVD分解的定义是，任意给定nxm大小的矩阵X，都可以将其分解为X=UΣVᵀ的形式，其中U是nxn大小的矩阵，Vᵀ是mxm大小矩阵，U和V均为正交矩阵(酉矩阵)，既满足UUᵀ = VVᵀ = E(单位阵)。而Σ是一个对角矩阵，Σ对角元素为X的奇异值(非负数)，其中的非零元素个数为X的秩的大小。
$\Sigma V^T$

求解U和V

下面给出求解U和V的方法：

首先求解V，我们需要构造AᵀA，此时AᵀA是一个实对称矩阵，必然可以进行特征分解，AᵀA的单位特征向量就是V矩阵，因此问题转化为对AᵀA做特征分解：
$A^T A=V \Sigma U^T U \Sigma V^T=V \Sigma^2 V^T$
同理U：XXᵀ的单位特征向量就是U矩阵
$A^T=U \Sigma V^T V \Sigma U^T=U \Sigma^2 U^T$
值得注意的是，r(AᵀA)=r(AAᵀ), 因此r(U)=r(V)，尽管他们的尺寸不同。

对于Σ，需要注意的是，为了满足UΣVᵀ能够相乘，Σ的尺寸应为nxm，但是由于Σ大多情况下并不满秩，因此我们只考虑Σ的尺寸为其对角线上非零元素的个数，这个个数就是X的秩的大小。

求解Σ

Σ的求法有两种，一种是通过求解AᵀA或AAᵀ的非零特征值的算数平方根(因为奇异值非负)，它们的结果应该是一样的(不用应该)。

另一种求法如下，待求解出V和U之后，AV与U每一列的比例系数都是一个奇异值：
$\Sigma V^T \Rightarrow A V=U \Sigma V^T V \Rightarrow A V=U \Sigma \Rightarrow A v_i=\sigma_i u_i \Rightarrow \sigma_i=A v_i / u_i$
$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-P7g9XPa1-1689527236057)(.\2.png)]$

2.应用部分

SVD分解的U矩阵的每一列称作左奇异向量，Vᵀ矩阵的每一行被称作右奇异向量，Σ的每一个对角元素是一个奇异值。
$U=\left[u_1, u_2, \cdots, u_n\right], \quad V^T=\left[\begin{array}{c} v_1^T \\ v_2^T \\ \vdots \\ v_m^T \end{array}\right], \Sigma=\left[\begin{array}{ccc} \sigma_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_m \end{array}\right]$
同特征分解类似，SVD分解的形式还可以表示如下：
$A=U\Sigma V^T=\sum_{\mathrm{i}=1}^{\mathrm{m}} \sigma_{\mathrm{i}} u_{\mathrm{i}} v_{\mathrm{i}}^{\mathrm{T}}$
可以注意到，uiviᵀ是一个列向量乘以一个行向量，结果是一个尺寸同A的秩为1的成分矩阵，而σ可以理解为该成分构成A的重要程度。依据这个，我们就可以通过抛弃不显著的σ来进行矩阵的低秩近似。比如说，我们可以通过只取前k大的奇异值和左右奇异向量来对原始矩阵A进行近似：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZYjueLaU-1689527236058)(.\3.png)]$

2.1图像压缩

低秩近似的一个经典应用就是图像压缩，给定一张图像，图像中可能包含噪声，通过SVD分解将图像的秩压缩到K来近似拟合原始图像。

(1) 以MNIST数据集为例，选取一张手写数字5的图像，对其进行奇异值分解得到的可视化结果：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-prRRq3Cp-1689527236058)(.\4.png)]$

对原始图像进行低秩近似。随着图像的秩不断升高，低秩矩阵会越来越逼近原始图像(从秩=1到秩=25)：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pharxOro-1689527236058)(.\5.png)]$

(2) 以celeba_hq数据集为例，选取一张人脸图像，对其进行奇异值分解得到的可视化结果：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nhhyF4mr-1689527236058)(.\6.png)]$

对原始图像进行低秩近似(从秩=1到秩=64)：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Jai8wUii-1689527236058)(.\7.png)]$

值得注意的是，当图像尺寸为nxm时，用秩=k去近似原图像，k需满足以下关系，才能真正实现压缩：
$\begin{aligned} \mathrm{nm} & >\mathrm{nk}+\mathrm{mk}+\mathrm{k} \\ \Rightarrow\mathrm{nm} & >(\mathrm{n}+\mathrm{m}+1) \mathrm{k} \\ \Rightarrow\mathrm{k} & <\frac{\mathrm{nm}}{\mathrm{n}+\mathrm{m}+1} \end{aligned}$
再举一个RGB图像压缩的例子：