前言

那么这里博主先安利一些干货满满的专栏了！

这两个都是博主在学习Linux操作系统过程中的记录，希望对大家的学习有帮助！

操作系统Operating Syshttps://blog.csdn.net/yu_cblog/category_12165502.html?spm=1001.2014.3001.5482Linux Syshttps://blog.csdn.net/yu_cblog/category_11786077.html?spm=1001.2014.3001.5482这两个是博主学习数据结构的同时，手撕模拟STL标准模版库各种容器的专栏。

STL源码剖析https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482手撕数据结构https://blog.csdn.net/yu_cblog/category_11490888.html

一、摘要

本次实验，通过学习边缘检测的原理，使用Matlab编程语言，完成对输出给定图像的边缘检测图像和完成车道线识别。

二、实验内容及目的

输出给定图像的边缘检测图像和完成车道线识别。

三、实验相关原理描述

边缘检测是一种图像处理技术，用于在图像中检测出物体或场景的边缘或轮廓。其原理是通过分析图像中的亮度或颜色变化来识别边缘位置。常用的边缘检测方法包括Sobel、Prewitt、Canny等。

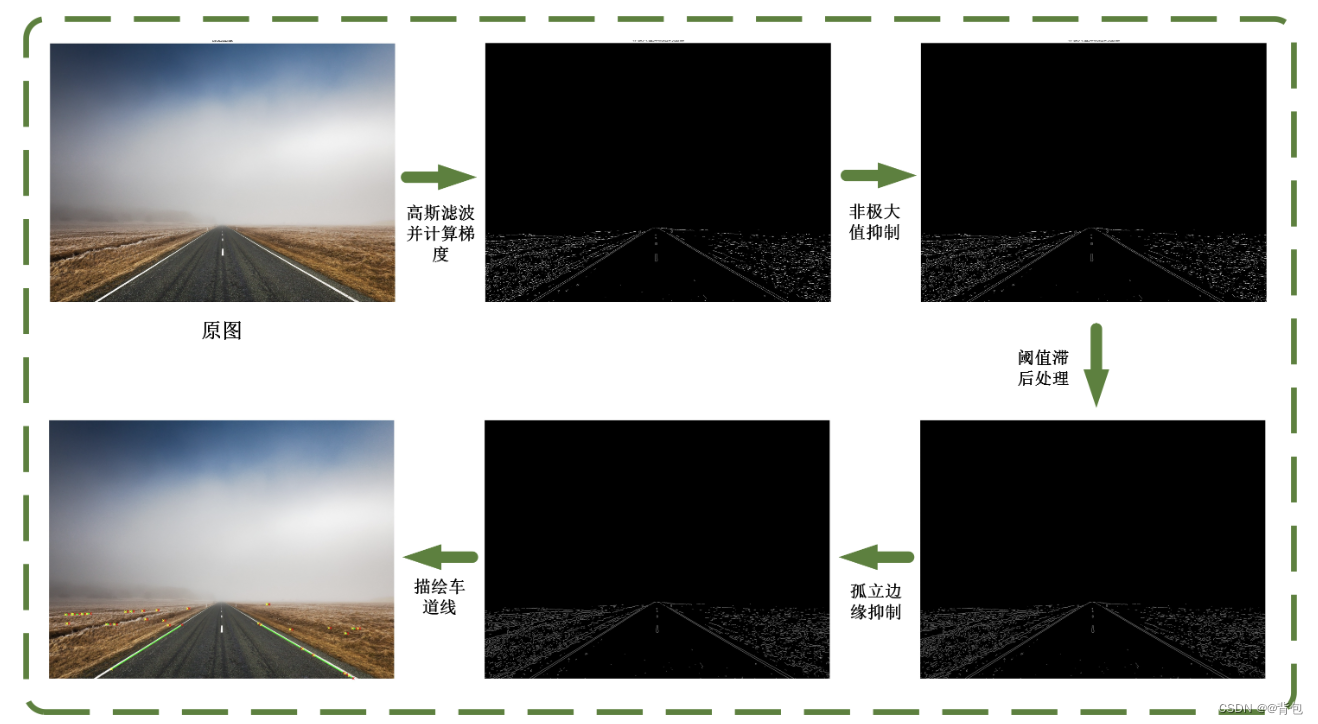
下面是本次实验主要流程：

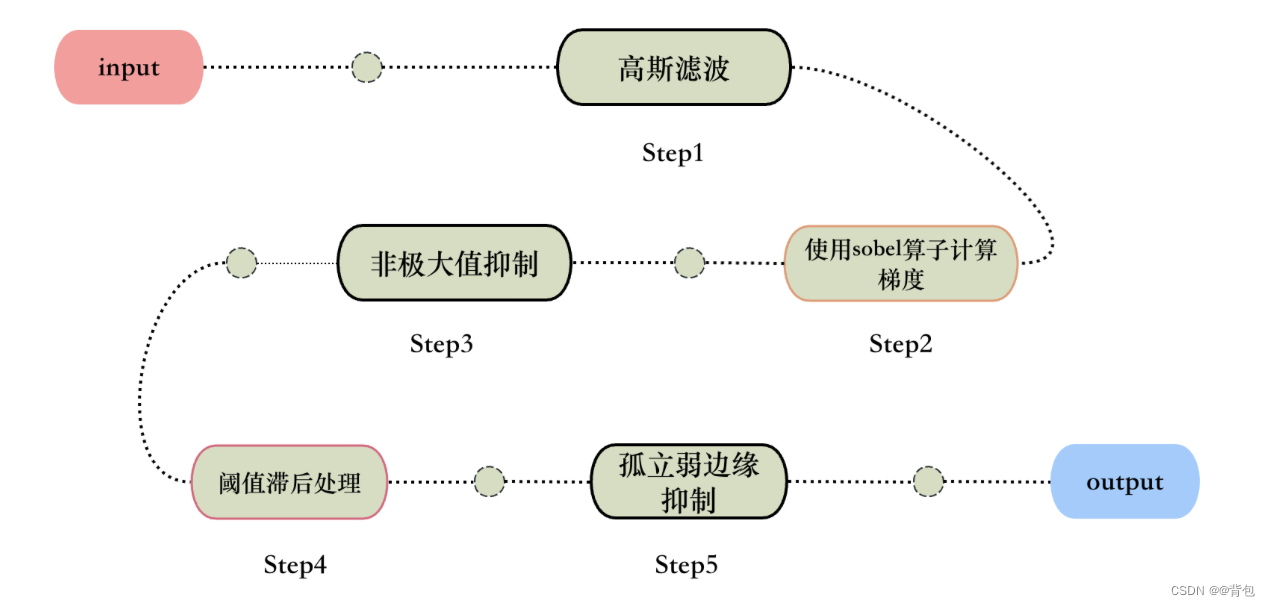
主要步骤原理

高斯滤波：

高斯滤波是一种常用的图像处理技术，用于平滑图像、去除噪声和边缘检测等应用。它基于高斯函数（也称为正态分布函数）的概念，通过对图像中的像素进行加权平均来实现平滑效果。

高斯滤波的公式如下：
$G(x, y) = \frac{1}{2\pi\sigma^2} \cdot e^{-\frac{x^2 + y^2}{2\sigma^2}}$

其中，G(x,y) 表示高斯滤波器在坐标(x,y) 处的权重值，σ 表示高斯函数的标准差，控制了滤波器的模糊程度。标准差越大，滤波器的模糊程度越高。

高斯滤波的原理是利用高斯函数的权重值对图像中的像素进行加权平均。滤波器的中心像素权重最大，越远离中心像素的像素权重越小。通过对邻近像素进行加权平均，可以使图像中的噪声平均化，并且能够保留图像的整体结构和边缘特征。

Sobel算子计算梯度：

水平方向的 Sobel 算子：
$G_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}\displaystyle$

垂直方向的Sobel算子：
$G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}$

这些模板是 3x3 的矩阵，分别对应着水平和垂直方向上的微分操作。通过将这些模板与图像进行卷积操作，可以得到图像在水平和垂直方向上的梯度值。

非极大值抑制：

非极大值抑制可以用来寻找像素点局部最大值，将非极大值所对应的灰度值置0，极大值点置1，这样可以剔除一大部分非边缘的像素点，从而得到一副二值图像，边缘理想状态下都为单像素边缘。
$\begin{array}{l} g_{u p}(i, j)=(1-t) \cdot g_{x y}(i, j+1)+t \cdot g_{x y}(i-1, j+1)\\ g_{\text {down }}(i, j)=(1-t) \cdot g_{x y}(i, j-1)+t \cdot g_{x y}(i+1, j-1) \end{array}$

四、实验过程和结果

% 读取图片
img = imread('图像路径');
imshow(img);
% 将图像转换为灰度
gray_img = rgb2gray(img);
% 高斯滤波
sigma = 2; % 高斯滤波器的标准差
gaussian_filtered_img = imgaussfilt(gray_img, sigma);
% 使用Sobel算子进行梯度计算
sobel_filtered_img = double(edge(gaussian_filtered_img, 'sobel'));
% 显示原始图像和处理后的图像
imshow(img); title('原始图像');
imshow(sobel_filtered_img); title('梯度计算后的图像');
% 定义梯度方向
directions = [-pi/2, -pi/4, 0, pi/4, pi/2, 3*pi/4, pi, -3*pi/4];

% 对每个像素，找到沿着梯度方向的两个相邻像素，计算它们的插值
nms_img = zeros(size(sobel_filtered_img));
for i=2:size(sobel_filtered_img,1)-1
    for j=2:size(sobel_filtered_img,2)-1
        % 找到最近的两个方向
        [~, index] = min(abs(directions - atan2d(-sobel_filtered_img(i,j), sobel_filtered_img(i,j+1))));
        if index == 1 || index == 5
            left = sobel_filtered_img(i-1,j-1);
            right = sobel_filtered_img(i+1,j+1);
        elseif index == 2 || index == 6
            left = sobel_filtered_img(i-1,j+1);
            right = sobel_filtered_img(i+1,j-1);
        elseif index == 3 || index == 7
            left = sobel_filtered_img(i,j-1);
            right = sobel_filtered_img(i,j+1);
        elseif index == 4 || index == 8
            left = sobel_filtered_img(i+1,j-1);
            right = sobel_filtered_img(i-1,j+1);
        end
        
        % 如果像素值是局部最大值，则保留
        if sobel_filtered_img(i,j) >= left && sobel_filtered_img(i,j) >= right
            nms_img(i,j) = sobel_filtered_img(i,j);
        end
    end
end

% 显示非极大值抑制后的图像
figure; imshow(nms_img); title('非极大值抑制后的图像');
% 阈值滞后处理
low_threshold = 0.05;
high_threshold = 0.2;
edge_map = zeros(size(nms_img));
edge_map(nms_img > high_threshold) = 1;
for i=2:size(nms_img,1)-1
    for j=2:size(nms_img,2)-1
        if (nms_img(i,j) > low_threshold) && (edge_map(i,j) == 0)
            if (edge_map(i-1,j-1) == 1) || (edge_map(i-1,j) == 1) || (edge_map(i-1,j+1) == 1) || (edge_map(i,j-1) == 1) || (edge_map(i,j+1) == 1) || (edge_map(i+1,j-1) == 1) || (edge_map(i+1,j) == 1) || (edge_map(i+1,j+1) == 1)
                edge_map(i,j) = 1;
            end
        end
    end
end
imshow(edge_map);

% 孤立弱边缘抑制
isolated_threshold = 1;
for i=2:size(edge_map,1)-1
    for j=2:size(edge_map,2)-1
        if (edge_map(i,j) == 1) && (sum(sum(edge_map(i-1:i+1,j-1:j+1))) <= isolated_threshold)
            edge_map(i,j) = 0;
        end
    end
end
imshow(edge_map);
% 车道线检测
% [m,n] = size(edge_map)
% x = [1600,0,0,1600];
% y = [1000,0,0,1000];
% mask = poly2mask(x,y,m,n);
% new_img = mask.*edge_map;
% imshow(new_img);

new_img = edge_map;
lines = HoughStraightRecognize(new_img);

hold on;
imshow(img);
for k = 1:length(lines)
% k = 7;
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
end

function lines = HoughStraightRecognize(BW)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%该函数为霍夫变换识别直线的函数
%input：图像（可以是二值图，也可以是灰度图）
%output：直线的struct结构，其结构组成为线段的两个端点
%以及在极坐标系下的坐标【rho，theta】
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    [H,T,R] = hough(BW);
    % imshow(H,[],'XData',T,'YData',R,...
    %             'InitialMagnification','fit');
    % xlabel('\theta'), ylabel('\rho');
        % axis on, axis normal, hold on;
    P  = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
    %x = T(P(:,2)); y = R(P(:,1));
    %plot(x,y,'s','color','white');
    lines = houghlines(BW,T,R,P,'FillGap',5,'MinLength',7);
    %FillGap 两个线段之间的距离，小于该值会将两个线段合并
    %MinLength 最小线段长度
end

实验过程所得到输出图像如下图所示：