题目：给你二叉树的根节点 root ，返回它节点值的中序遍历。
要求：非递归实现。

     1
    /  \
   2    3
  / \  / \
 4  5  6  7

中序遍历结果为：

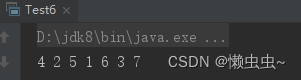
4 2 5 1 6 3 7

这里考察中序遍历思想，使用Stack的后进先出特性输出结果。
TreeNode树状结构

@Data
public class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;

    public TreeNode(int value) {
        this.value = value;
    }
}

buildTree构造树形结构数据

private static TreeNode buildTree() {
        // 定义树形结构数据最大值为7
        TreeNode[] nodes = new TreeNode[7];
        for (int i = 0; i < nodes.length; i++) {
            // 树值从1开始
            nodes[i] = new TreeNode(i + 1);
            int parent = (i + 1) / 2 - 1;
            if (parent >= 0) {
                // 偶数倍，放到左子树，注意i是从0开始算的
                if (i + 1 == 2 * (parent + 1)) {
                    nodes[parent].setLeft(nodes[i]);
                } else {
                    // 奇数倍，放到右子树，注意i是从0开始算的
                    nodes[parent].setRight(nodes[i]);
                }
            }
        }
        return nodes[0];
    }

构造后的图形化展示结果，注意程序不会输出左右斜杠哦~

     1
    /  \
   2    3
  / \  / \
 4  5  6  7

实现算法方案一：借助栈的特性，迭代实现

public static List<TreeNode> traversAl1(TreeNode root) {
        // 中序遍历
        List<TreeNode> myTreeNodeList = new ArrayList();
        Stack<TreeNode> myTreeNodeStack = new Stack<>();
        TreeNode tempNode = root;
        while(tempNode != null || !myTreeNodeStack.isEmpty()){
            // 循环将左子树放入栈
            while(tempNode != null){
                myTreeNodeStack.push(tempNode);
                tempNode = tempNode.getLeft();
            }
            // 对左子树出栈，后进先出
            TreeNode resultNode = myTreeNodeStack.pop();
            // 将结果赛入结果list中
            myTreeNodeList.add(resultNode);
            // 将右子树替换tempNode 
            tempNode = resultNode.getRight();
        }
        return myTreeNodeList;
    }

实现算法方案二：递归实现

 /**
     * 递归实现中序遍历
     *
     * @param root
     * @return
     */
    public static List<TreeNode> traversAl12(TreeNode root){
        List<TreeNode> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }

    public static void inorder(TreeNode root, List<TreeNode> res){
        if(root == null){
            return;
        }
        inorder(root.getLeft(),res);
        res.add(root);
        inorder(root.getRight(),res);
    }

整体代码

public class Test6 {
    public static void main(String[] args) {
        //printTree(traversAl1(buildTree()));// 利用栈迭代实现
        printTree(traversAl12(buildTree())); // 利用递归实现
    }

    public static void printTree(List<TreeNode> nodeList) {
        nodeList.forEach(node -> System.out.print(node.getValue() + " "));
    }

    private static TreeNode buildTree() {
        TreeNode[] nodes = new TreeNode[7];
        for (int i = 0; i < nodes.length; i++) {
            nodes[i] = new TreeNode(i + 1);
            int parent = (i + 1) / 2 - 1;
            if (parent >= 0) {
                if (i + 1 == 2 * (parent + 1)) {
                    nodes[parent].setLeft(nodes[i]);
                } else {
                    nodes[parent].setRight(nodes[i]);
                }
            }
        }
        return nodes[0];
    }

    /**
     * 迭代实现中序遍历
     *
     * @param root
     * @return
     */
    public static List<TreeNode> traversAl1(TreeNode root) {
        // 中序遍历
        List<TreeNode> myTreeNodeList = new ArrayList();
        Stack<TreeNode> myTreeNodeStack = new Stack<>();
        TreeNode tempNode = root;
        // 当根节点不为空或者栈不为空的时候进入循环
        while(tempNode != null || !myTreeNodeStack.isEmpty()){
            // 当中间节点不为空的时候把中间节点放入栈，并指向左子树，一直找到最左的节点，放入栈中再依次弹出栈
            while(tempNode != null){
                myTreeNodeStack.push(tempNode);
                tempNode = tempNode.getLeft();
            }
            TreeNode resultNode = myTreeNodeStack.pop();
            myTreeNodeList.add(resultNode);
            tempNode = resultNode.getRight();
        }
        return myTreeNodeList;
    }

    /**
     * 递归实现中序遍历
     *
     * @param root
     * @return
     */
    public static List<TreeNode> traversAl12(TreeNode root){
        List<TreeNode> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }

    public static void inorder(TreeNode root, List<TreeNode> res){
        if(root == null){
            return;
        }
        inorder(root.getLeft(),res);
        res.add(root);
        inorder(root.getRight(),res);
    }
}

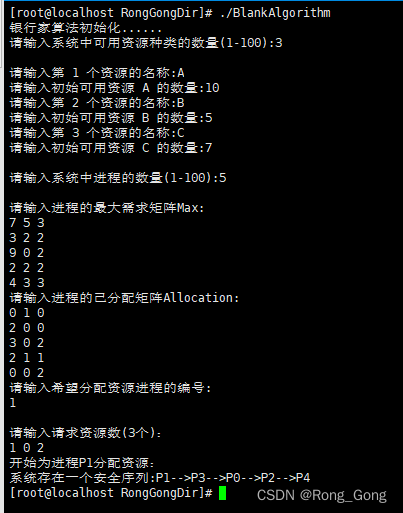
测试结果