文章目录

一：图像分割概述
二：阈值分割
- （1）概述
- （2）阈值化
- （3）基于灰度直方图的阈值选择
- - A：原理
  - B：程序
- （4）基于模式分类思路的阈值选择
- - A：原理
  - B：最大类间方差法（OTSU）
  - C：最大熵法
  - D：最小误差法
- （5）其他阈值分割方法
- - A：基于迭代运算的阈值选择
  - B：基于模糊理论的阈值选择
三：边界分割
- （1）基于梯度的边界闭合
- （2）霍夫（Hough）变换
- （3）边界跟踪

一：图像分割概述

图像分割：在对图像的研究和应用中，人们往往仅对图像中的某些目标感兴趣，这些目标通常对应图像中具有特定性质的区域。图像分割是指把一幅图像分成不同的具有特定性质区域的图像处理技术，将这些区域分离提取出来，以便进一步提取特征和理解

在这里插入图片描述

图像分割方法多种多样，常用的技术包括：

基于阈值：根据像素的灰度值或者颜色信息，将图像分成不同的区域。这种方法简单直观，适用于一些简单的场景，但对于复杂图像可能效果不佳
基于边缘检测：通过检测图像中的边缘信息，将图像分割成不同的区域。常用的边缘检测算法包括Canny边缘检测和Sobel算子等
基于区域生长：从种子像素开始，根据一定的相似性准则，逐渐将相邻像素合并为一个区域，直到满足停止准则。这种方法对于具有明显区域边界的图像效果较好
基于图割：将图像分割问题转化为图论中的图割问题，通过最小化图中的能量函数来实现分割。这种方法可以捕捉到像素之间的全局关系，具有较好的准确性
基于深度学习：近年来，深度学习技术在图像分割中取得了显著的进展。通过使用深度卷积神经网络（CNN）或者全卷积网络（FCN），可以学习到图像的语义信息，并生成像素级的分割结果

图像分割在很多应用中都起着关键作用。例如，在医学图像处理中，图像分割可以用于识别和定位肿瘤或病变区域，帮助医生进行诊断和治疗决策。在自动驾驶领域，图像分割可用于识别道路、行人和交通标志等，并提供有关环境的关键信息。此外，图像分割还在图像编辑、目标检测、虚拟现实和增强现实等领域有广泛的应用

二：阈值分割

（1）概述

阈值分割：是图像分割中最简单和常用的方法之一。它基于像素的灰度值或颜色信息，将图像中的像素分成两个或多个不同的区域。阈值分割的基本思想是选择一个阈值，将图像中的像素分为高于或低于该阈值的两个类别。步骤如下

灰度化：将彩色图像转换为灰度图像，以便在单个灰度通道上进行处理
选择阈值：选择一个适当的阈值来将图像分割成不同的区域。阈值可以根据经验、直方图分析、自适应方法等进行选择
分割图像：根据所选择的阈值，将图像中的像素分为两个或多个类别。通常情况下，像素值高于阈值的被分配到一个类别，低于阈值的被分配到另一个类别

阈值分割原理如下

$y)=\left\{\begin{array}{ll}1 & f(x, y) \geq T \\0 & f(x, y)<T\end{array}\right.$

其中 $f (x, y)$ 为原始图像， $g (x, y)$ 为结果图像（二值）， $T$ 为阈值。显然，阈值的选取决定了二值化效果的好坏

（2）阈值化

阈值化：是图像处理中的一种常用技术，用于将图像中的像素分成两个或多个不同的类别，例如将图像分为前景和背景。阈值化基于像素的灰度值或颜色信息，通过设置一个阈值来决定像素属于哪个类别。在阈值化过程中，像素根据其与阈值的关系进行分类。通常情况下，如果像素值高于阈值，则被归为一个类别（例如前景），否则归为另一个类别（例如背景）。阈值化的目的是根据图像的特性将图像进行简化或分割，以便于后续处理或分析。阈值化常用于以下应用场景

目标检测：通过将图像分割成前景和背景，可以更容易地提取感兴趣的目标区域，并进行后续的目标检测和识别
图像分割：阈值化可以将图像分割成不同的区域，例如将肿瘤区域从医学图像中分割出来，或将物体从复杂的背景中分离出来
图像增强：通过选择适当的阈值，可以增强图像的某些特征，例如增强图像的边缘信息或改善图像的对比度
物体计数：通过将图像中的像素分成前景和背景，可以对前景像素进行计数，从而实现物体数量的估计或统计

阈值化的方法和技术有很多种，例如

上阈值化：灰度值大于等于阈值的所有像素作为前景像素，其余像素作为背景像素
下阈值化：灰度值小于等于阈值的所有像素作为前景像素
内阈值化：确定一个较小的阈值和一个较大的阈值，灰度值介于二者之间的像素作为前景像素
外阈值化：灰度值介于小阈值和大阈值之外的像素作为前景像素

（3）基于灰度直方图的阈值选择

A：原理

基于灰度直方图的阈值选择：它基于图像的灰度分布特性来选择适当的阈值，将图像分割成不同的区域

灰度直方图：首先，计算图像的灰度直方图，即统计不同灰度级别的像素数量。灰度直方图可以反映图像中各个灰度级别的分布情况
阈值选择：根据灰度直方图的形状和特点，选择一个适当的阈值来将图像分割成不同的区域。常见的阈值选择方法包括以下几种
- 单峰阈值法：适用于图像灰度直方图呈现单个明显峰值的情况。阈值通常选择在峰值处或峰值附近
- 双峰阈值法：适用于图像灰度直方图呈现双个明显峰值的情况，其中一个峰值代表背景，另一个峰值代表目标或前景。阈值选择通常在两个峰值之间的谷底处
- Otsu’s 方法：Otsu’s 方法是一种基于最大类间方差的自适应阈值选择方法。它能够自动选择一个阈值，使得分割后的图像的前景和背景之间的类间方差最大化
- 高斯混合模型（GMM）：GMM 方法假设图像中的像素灰度值服从多个高斯分布，通过拟合多个高斯分布，找到各个分布之间的转折点作为阈值
分割图像：根据选择的阈值，将图像中的像素分成两个或多个类别，通常是将像素灰度值高于阈值的归为一个类别，低于阈值的归为另一个类别

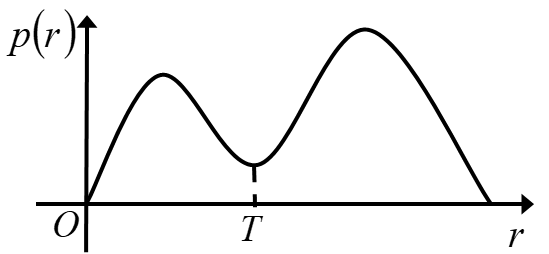
例如下图，图像的灰度直方图为双峰分布，表明图像的内容大致为两部分，分别为灰度分布的两个山峰的附近，则选择阈值为两峰间的谷底点对应灰度值。这适用于图像中前景与背景灰度差别明显，且各占一定比例的情形，是一种特殊的方法。若图像整体直方图不具有双峰或多峰特性，可以考虑局部范围内应用

在这里插入图片描述

B：程序

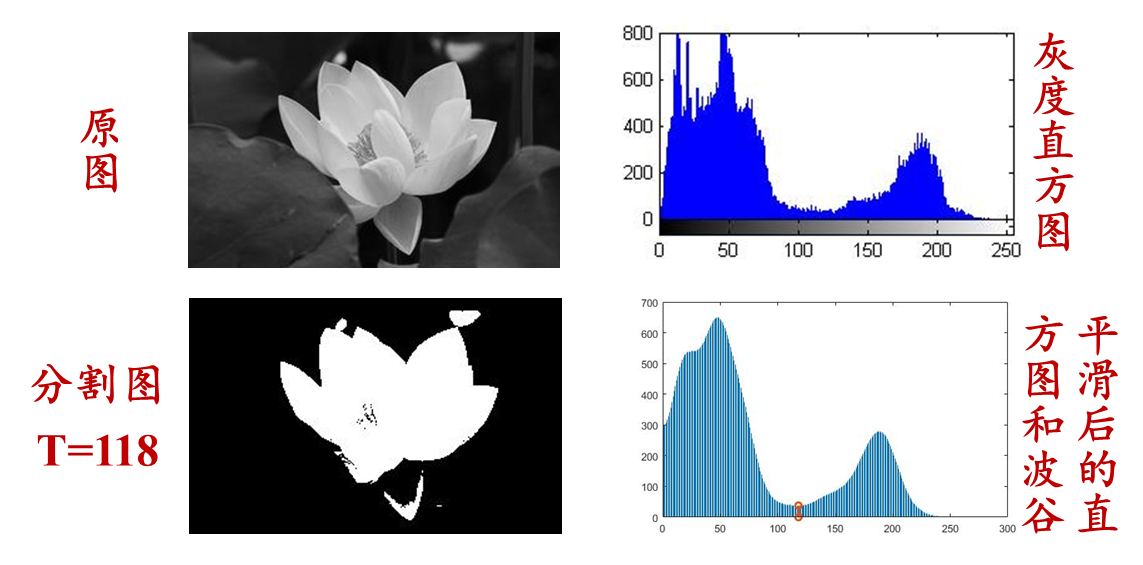
如下：实现基于双峰分布的直方图选择阈值，分割图像

重点在于找到直方图的峰和波谷，但直方图通常是不平滑的，因此，首先要平滑直方图，再去搜索峰和谷
程序设计中，将直方图中相邻三个灰度的频数相加求平均作为中间灰度对应的频数，不断平滑直方图，直至成为双峰分布
也可以采用其他方法确定峰谷

在这里插入图片描述

matlab实现：

clear,clc,close all;
Image=rgb2gray(imread('lotus1.jpg'));
figure,imshow(Image),title('原始图像');
imhist(Image);
hist1=imhist(Image);
hist2=hist1;
iter=0;
while 1
    [is,peak]=Bimodal(hist1);
    if is==0
        hist2(1)=(hist1(1)*2+hist1(2))/3;
        for j=2:255
            hist2(j)=(hist1(j-1)+hist1(j)+hist1(j+1))/3;
        end
        hist2(256)=(hist1(255)+hist1(256)*2)/3;
        hist1=hist2;
        iter=iter+1;
        if iter>1000
            break;
        end
    else
        break;
    end
end

[trough,pos]=min(hist1(peak(1):peak(2)));
thresh=pos+peak(1);
figure,stem(1:256,hist1,'Marker','none');
hold on
stem([thresh,thresh],[0,trough],'Linewidth',2);
hold off
result=zeros(size(Image));
result(Image>thresh)=1;
figure,imshow(result),title('基于双峰直方图的阈值化');
imwrite(result,'bilotus1.jpg');   

function [is,peak]=Bimodal(histgram)
    count=0;
    for j=2:255
        if histgram(j-1)<histgram(j) && histgram(j+1)<histgram(j)
            count=count+1;
            peak(count)=j;
            if count>2 
                is=0;
                return;
            end
        end
    end
    if count==2
        is=1;
    else
        is=0;
    end
end

import cv2
import numpy as np
import matplotlib.pyplot as plt

def Bimodal(histgram):
    count = 0
    peak = []
    for j in range(1, 255):
        if histgram[j-1] < histgram[j] and histgram[j+1] < histgram[j]:
            count += 1
            peak.append(j)
            if count > 2:
                return 0, peak
    if count == 2:
        return 1, peak
    else:
        return 0, peak

# 读取图像并转换为灰度图像
image = cv2.imread('lotus1.jpg')
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 显示原始图像
plt.figure()
plt.imshow(gray_image, cmap='gray')
plt.title('原始图像')

# 绘制灰度直方图
plt.figure()
plt.hist(gray_image.ravel(), bins=256, color='gray')
plt.title('灰度直方图')

# 计算灰度直方图
hist1 = cv2.calcHist([gray_image], [0], None, [256], [0, 256])
hist2 = hist1.copy()
iter = 0
while True:
    is_bimodal, peak = Bimodal(hist1)
    if is_bimodal == 0:
        hist2[0] = (hist1[0]*2 + hist1[1]) / 3
        for j in range(1, 255):
            hist2[j] = (hist1[j-1] + hist1[j] + hist1[j+1]) / 3
        hist2[255] = (hist1[254] + hist1[255]*2) / 3
        hist1 = hist2
        iter += 1
        if iter > 1000:
            break
    else:
        break

# 根据双峰直方图选择阈值
trough, pos = np.min(hist1[peak[0]:peak[1]]), np.argmin(hist1[peak[0]:peak[1]])
thresh = pos + peak[0]

# 绘制带阈值的直方图
plt.figure()
plt.stem(np.arange(256), hist1, markerfmt='none')
plt.axvline(x=thresh, ymin=0, ymax=trough, linewidth=2)
plt.title('双峰直方图阈值化')

# 基于阈值进行图像分割
result = np.zeros_like(gray_image)
result[gray_image > thresh] = 255

# 显示分割结果
plt.figure()
plt.imshow(result, cmap='gray')
plt.title('基于双峰直方图的阈值化')

# 保存结果图像
cv2.imwrite('bilotus1.jpg', result)

# 显示所有图像
plt.show()

（4）基于模式分类思路的阈值选择

A：原理

基于模式分类思路的阈值选择：是一种根据像素的特征模式来选择阈值的方法。它基于对图像中不同像素的特征进行分析和分类，以确定最佳的阈值，将图像分割为不同的区域。以下是基于模式分类思路的阈值选择的基本步骤

计算特征：首先，对图像中的像素进行特征计算。常见的特征包括像素灰度值、梯度、纹理等
划分模式：将像素根据特征的不同模式进行分类。根据特定的阈值，将像素分为不同的模式类别。例如，可以将像素分为背景和前景模式类别
计算类别间差异度量：对不同的模式类别计算其间的差异度量，比如类别之间的平均灰度差异、方差等。这些度量反映了不同类别之间的分离程度
选择最佳阈值：根据类别间的差异度量，选择最佳的阈值作为分割图像的阈值。通常，较大的类别间差异度量意味着更好的分割效果
应用阈值：使用选择的阈值将图像分割为不同的区域。将像素灰度值与阈值进行比较，并根据比较结果将像素分为不同的类别

基于模式分类思路的阈值选择方法可以适应不同的图像特征和分割要求。通过对像素进行特征分析和模式分类，该方法能够根据图像的内在特性选择最佳的阈值，从而实现有效的图像分割。然而，选择适当的特征和合适的模式分类算法是该方法的关键，需要根据具体问题进行选择和优化

B：最大类间方差法（OTSU）

最大类间方差法（OTSU）：是一种自适应的图像阈值选择方法，用于将图像分割成前景和背景两个区域。该方法通过最大化图像两个类别之间的类间方差，来选择最佳的阈值，以实现最佳的分割效果。下面是最大类间方差法的基本原理

计算直方图：首先，计算图像的灰度直方图，统计不同灰度级别的像素数量
计算类内方差：对于每个可能的阈值（0到255），将图像分成前景和背景两个类别，并计算两个类别的类内方差。类内方差反映了同一类别内像素灰度值的变化程度
计算类间方差：通过将图像分割为前景和背景两个类别，计算这两个类别之间的类间方差。类间方差反映了两个类别之间的灰度差异程度
最大化类间方差：遍历所有可能的阈值，找到使类间方差最大的阈值，即最佳阈值。最大化类间方差意味着前景和背景之间的差异最大化，从而实现最佳的图像分割效果
应用阈值：使用选择的最佳阈值将图像分割为前景和背景两个区域。将像素灰度值与阈值进行比较，并根据比较结果将像素分为不同的类别

两类方差

$\sigma_{o}^{2}=\frac{1}{p_{o}} \sum_{i=0}^{T} p_{i}\left(i-\mu_{o}\right)^{2} \quad \sigma_{B}^{2}=\frac{1}{p_{B}} \sum_{i=T+1}^{L-1} p_{i}\left(i-\mu_{B}\right)^{2}$

类内方差和类间方差

$\begin{array}{l}\sigma_{i n}^{2}=p_{O} \cdot \sigma_{o}^{2}+p_{B} \cdot \sigma_{B}^{2} \\\sigma_{1}^{2}=p_{o} \times\left(\mu_{o}-\mu\right)^{2}+p_{B} \times\left(\mu_{B}-\mu\right)^{2}\end{array}$

如下

在这里插入图片描述

matlab实现

Image=rgb2gray(imread('lotus1.jpg'));
figure,imshow(Image),title('原始图像');
T=graythresh(Image);
result=im2bw(Image,T);
figure,imshow(result),title('OTSU方法二值化图像 ');
% imwrite(result,'lotus1otsu.jpg');

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为灰度图像
image = cv2.imread('lotus1.jpg')
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 显示原始图像
plt.figure()
plt.imshow(gray_image, cmap='gray')
plt.title('原始图像')

# 使用Otsu方法选择阈值
_, threshold = cv2.threshold(gray_image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)

# 对图像进行二值化
result = cv2.bitwise_and(gray_image, threshold)

# 显示二值化结果
plt.figure()
plt.imshow(result, cmap='gray')
plt.title('OTSU方法二值化图像')

# 保存结果图像
# cv2.imwrite('lotus1otsu.jpg', result)

# 显示所有图像
plt.show()

C：最大熵法

最大熵法：是一种常用的图像分割方法之一，用于将图像分割为不同的区域。它基于信息熵的概念，通过最大化图像中各个区域的熵来选择最佳的分割结果。以下是最大熵法的基本原理

定义图像熵：首先，计算图像的全局熵，即将整个图像视为一个区域，计算其熵。图像熵是表示图像灰度分布的随机性和不确定性的度量
定义局部熵：将图像划分为不同的区域，并计算每个区域的局部熵。局部熵反映了各个区域内像素灰度分布的随机性和不确定性
计算条件熵：根据图像的分割结果，计算每个区域的条件熵。条件熵是指在已知区域分割情况下，对于每个区域内的像素，其灰度分布的随机性和不确定性
定义目标函数：定义一个目标函数，如最大熵准则函数，将全局熵、局部熵和条件熵组合起来。目标函数的目标是最大化分割结果的熵，以达到最佳的图像分割效果
寻找最佳分割：通过迭代优化方法或其他优化算法，搜索最佳的分割结果。最终目标是找到使目标函数最大化的最佳区域分割

最大熵法能够自适应地选择图像的最佳分割结果，无需预先了解图像的特征或背景信息。通过最大化图像的熵，该方法能够实现在不同区域间的边界上找到最佳的分割结果，适用于不同类型的图像分割任务。需要注意的是，最大熵法在实际应用中可能需要考虑一些因素，如计算复杂度、初始分割结果、优化算法等。根据具体的应用需求和图像特性，可能需要结合其他的图像处理技术和算法，以提高分割的准确性和鲁棒性

如下

在这里插入图片描述

matlab实现：

clear,clc,close all;
Image=rgb2gray(imread('fruit.jpg'));
figure,imshow(Image),title('原始图像');
hist=imhist(Image);
bottom=min(Image(:))+1;
top=max(Image(:))+1;
J=zeros(256,1);
for t=bottom+1:top-1
    po=sum(hist(bottom:t));
    pb=sum(hist(t+1:top));
    ho=0;
    hb=0;
    for j=bottom:t
        ho=ho-log(hist(j)/po+0.01)*hist(j)/po;
    end
    for j=t+1:top
        hb=hb-log(hist(j)/pb+0.01)*hist(j)/pb;
    end
    J(t)=ho+hb;        
end
[maxJ,pos]=max(J(:));
result=zeros(size(Image));
result(Image>pos)=1;
figure,imshow(result);

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为灰度图像
image = cv2.imread('fruit.jpg')
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 显示原始图像
plt.figure()
plt.imshow(gray_image, cmap='gray')
plt.title('原始图像')

# 计算图像直方图
hist = cv2.calcHist([gray_image], [0], None, [256], [0, 256])

bottom = np.min(gray_image) + 1
top = np.max(gray_image) + 1
J = np.zeros((256, 1))

for t in range(bottom + 1, top):
    po = np.sum(hist[bottom:t])
    pb = np.sum(hist[t+1:top])
    ho = 0
    hb = 0
    for j in range(bottom, t):
        ho = ho - np.log(hist[j] / po + 0.01) * hist[j] / po
    for j in range(t+1, top):
        hb = hb - np.log(hist[j] / pb + 0.01) * hist[j] / pb
    J[t] = ho + hb

maxJ, pos = np.max(J), np.argmax(J)

# 分割图像
result = np.zeros_like(gray_image)
result[gray_image > pos] = 255

# 显示分割结果
plt.figure()
plt.imshow(result, cmap='gray')

# 显示所有图像
plt.show()

D：最小误差法

最小误差法：是一种常用的图像分割方法之一，用于将图像分割为不同的区域。它基于像素灰度值的统计特性，通过最小化分割中的误差来选择最佳的阈值，以实现最佳的分割效果。以下是最小误差法的基本原理

计算直方图：首先，计算图像的灰度直方图，统计不同灰度级别的像素数量
初始化阈值：选择一个初始阈值，可以是根据经验确定的值，或者根据某种准则选择的初步估计
计算平均灰度值：根据当前阈值，将图像分割为两个区域：低于阈值的区域为背景，高于阈值的区域为前景。计算两个区域的平均灰度值
更新阈值：根据前一步计算得到的平均灰度值，更新阈值。常见的更新方法包括取两个区域平均灰度值的平均值或加权平均值
计算误差：根据更新后的阈值，计算分割中的误差。误差可以根据不同的准则定义，如均方误差、交叉熵等
重复步骤3至5：迭代执行步骤3至5，直到达到收敛条件，如阈值的变化小于某个阈值，或者误差不再明显改变
最佳阈值选择：根据达到收敛的结果，选择最佳的阈值作为图像的分割阈值

最小误差法能够根据图像的灰度分布特性自适应地选择最佳的分割阈值。通过迭代优化的过程，该方法通过最小化分割中的误差来实现最佳的图像分割效果。需要注意的是，最小误差法的性能受到初始阈值和收敛条件的选择的影响。选择合适的初始阈值和适当的收敛条件可以帮助提高分割的准确性和效率。此外，对于复杂的图像场景，可能需要结合其他的图像处理技术和算法，以提高分割的准确性和鲁棒性

如下

在这里插入图片描述

matlab实现：

clear,clc,close all;
Image=rgb2gray(imread('fruit.jpg'));
figure,imshow(Image),title('原始图像');
hist=imhist(Image);
bottom=min(Image(:))+1;
top=max(Image(:))+1; 
J=zeros(256,1);
J=J+100000;
alpha=0.25;
scope=find(hist>5);
minthresh=scope(1);
maxthresh=scope(end);
for t=minthresh+1:maxthresh-1
    miuo=0;
    sigmaho=0;
    for j=bottom:t
        miuo=miuo+hist(j)*double(j);
    end
    pixelnum=sum(hist(bottom:t));
    miuo=miuo/pixelnum;
    for j=bottom:t
        sigmaho=sigmaho+(double(j)-miuo)^2*hist(j);
    end
    sigmaho=sigmaho/pixelnum;
    
    miub=0;
    sigmahb=0;
    for j=t+1:top
        miub=miub+hist(j)*double(j);
    end
    pixelnum=sum(hist(t+1:top));
    miub=miub/pixelnum;
    for j=t+1:top
        sigmahb=sigmahb+(double(j)-miub)^2*hist(j);
    end
    sigmahb=sigmahb/pixelnum;
    
    Epsilonb=0;
    Epsilono=0;
    for j=bottom:t
        pb=exp(-(double(j)-miub)^2/(sigmahb*2+eps))/(sqrt(2*pi*sigmahb)+eps);
        Epsilonb=Epsilonb+pb;
    end
    for j=t+1:top        
        po=exp(-(double(j)-miuo)^2/(sigmaho*2+eps))/(sqrt(2*pi*sigmaho)+eps);
        Epsilono=Epsilono+po;
    end
    J(t)=alpha*Epsilono+(1-alpha)*Epsilonb;
end
[minJ,pos]=min(J(:));
result=zeros(size(Image));
result(Image>pos)=1;
figure,imshow(result),title('最小误差阈值法');

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为灰度图像
image = cv2.imread('fruit.jpg')
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 显示原始图像
plt.figure()
plt.imshow(image_gray, cmap='gray')
plt.title('原始图像')

# 计算直方图
hist = cv2.calcHist([image_gray], [0], None, [256], [0, 256])

bottom = np.min(image_gray) + 1
top = np.max(image_gray) + 1
J = np.zeros((256, 1)) + 100000
alpha = 0.25

# 找到直方图中像素数大于5的范围
scope = np.where(hist > 5)[0]
minthresh = scope[0]
maxthresh = scope[-1]

for t in range(minthresh + 1, maxthresh):
    miuo = 0
    sigmaho = 0

    for j in range(bottom, t):
        miuo += hist[j] * j

    pixelnum = np.sum(hist[bottom:t])
    miuo /= pixelnum

    for j in range(bottom, t):
        sigmaho += (j - miuo) ** 2 * hist[j]

    sigmaho /= pixelnum

    miub = 0
    sigmahb = 0

    for j in range(t + 1, top):
        miub += hist[j] * j

    pixelnum = np.sum(hist[t + 1:top])
    miub /= pixelnum

    for j in range(t + 1, top):
        sigmahb += (j - miub) ** 2 * hist[j]

    sigmahb /= pixelnum

    Epsilonb = 0
    Epsilono = 0

    for j in range(bottom, t):
        pb = np.exp(-(j - miub) ** 2 / (sigmahb * 2 + np.finfo(float).eps)) / (np.sqrt(2 * np.pi * sigmahb) + np.finfo(float).eps)
        Epsilonb += pb

    for j in range(t + 1, top):
        po = np.exp(-(j - miuo) ** 2 / (sigmaho * 2 + np.finfo(float).eps)) / (np.sqrt(2 * np.pi * sigmaho) + np.finfo(float).eps)
        Epsilono += po

    J[t] = alpha * Epsilono + (1 - alpha) * Epsilonb

minJ, pos = np.min(J), np.argmin(J)
result = np.zeros(image_gray.shape)

# 根据阈值分割图像
result[image_gray > pos] = 1

# 显示分割结果
plt.figure()
plt.imshow(result, cmap='gray')
plt.title('最小误差阈值法')

plt.show()

（5）其他阈值分割方法

A：基于迭代运算的阈值选择

基于迭代运算的阈值选择：是一种常用的图像分割方法，它通过反复迭代来求解最佳的阈值，以将图像分割为目标和背景两部分。该方法的基本思想是将图像的灰度值根据阈值划分为两个区域，并根据两个区域的平均灰度值来更新阈值，直到满足某个终止条件为止。一般步骤如下

选择初始阈值：可以是任意合理的值，例如图像灰度值的中值
根据选定的阈值，将图像分为两个区域：一个区域包含大于阈值的像素，另一个区域包含小于或等于阈值的像素
计算两个区域的平均灰度值：一个是大于阈值的像素的平均灰度值，另一个是小于或等于阈值的像素的平均灰度值
将平均灰度值的平均作为新的阈值
重复步骤2至步骤4，直到满足某个停止准则：常用的停止准则包括阈值的变化小于某个预设阈值或迭代次数达到预设值
最终得到的阈值即为最佳阈值，将图像根据该阈值进行二值化分割

基于迭代运算的阈值分割方法简单易懂，并且适用于大部分图像，特别是对于灰度直方图具有双峰特征的图像。然而，该方法对图像噪声和灰度分布不均匀的情况可能不够稳定和准确，因此在实际应用中可能需要进行参数调整和优化

如下

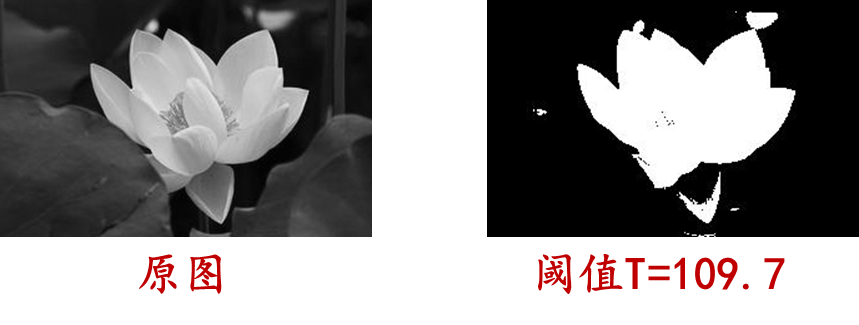
在这里插入图片描述

matlab实现：

clear,clc,close all;
Image=im2double(rgb2gray(imread('lotus1.jpg')));
figure,imshow(Image),title('原始图像');
T=(max(Image(:))+min(Image(:)))/2;
equal=false;
while ~equal
    rb=find(Image>=T);
    ro=find(Image<T);
    NewT=(mean(Image(rb))+mean(Image(ro)))/2;
    equal=abs(NewT-T)<1/256;
    T=NewT;
end
result=im2bw(Image,T);
figure,imshow(result),title('迭代方法二值化图像 ');

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为灰度图像
image = cv2.imread('lotus1.jpg')
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
image_gray = image_gray.astype(float) / 255.0

# 显示原始图像
plt.figure()
plt.imshow(image_gray, cmap='gray')
plt.title('原始图像')

# 初始化阈值
T = (np.max(image_gray) + np.min(image_gray)) / 2
equal = False

while not equal:
    rb = np.where(image_gray >= T)
    ro = np.where(image_gray < T)
    NewT = (np.mean(image_gray[rb]) + np.mean(image_gray[ro])) / 2
    equal = abs(NewT - T) < 1 / 256
    T = NewT

# 根据阈值进行二值化
result = (image_gray >= T).astype(np.uint8)

# 显示二值化结果
plt.figure()
plt.imshow(result, cmap='gray')
plt.title('迭代方法二值化图像')

plt.show()

B：基于模糊理论的阈值选择

基于模糊理论的阈值选择：与传统二值化方法只使用一个固定阈值不同，基于模糊理论的阈值分割方法使用模糊集合来描述像素属于目标或背景的隶属度，从而更灵活地处理图像中的不确定性和复杂性。模糊度表示一个模糊集的模糊程度，模糊熵是一种度量模糊度的数量指标，用模糊熵作为目标函数,求解最佳阈值。步骤如下

确定模糊化方法：将原始图像模糊化处理，常见的模糊化方法包括高斯模糊、均值模糊等。模糊化有助于降低噪声的影响，并将图像转化为模糊集合
确定隶属函数：为图像中的每个像素定义隶属函数，隶属函数描述了该像素属于目标或背景的程度。常见的隶属函数包括三角隶属函数、高斯隶属函数等
确定模糊阈值：选择一个合适的模糊阈值，将像素根据隶属函数划分为目标或背景。这个过程相当于传统二值化中的阈值确定，但基于模糊理论，阈值变得模糊，允许像素在目标和背景之间具有模糊的隶属度
模糊化反演：根据确定的模糊阈值，通过模糊化反演将模糊集合映射回到二值图像，得到最终的分割结果

基于模糊理论的阈值分割方法相比传统二值化方法具有更强的适应性和鲁棒性，特别适用于图像中目标和背景之间存在模糊边界的情况。这种方法可以在处理噪声较多或光照不均匀的图像时表现更好，但在一些情况下可能需要更多的计算资源。因此，在应用时需要根据具体情况选择适当的图像分割方法

如下

在这里插入图片描述

matlab实现：

clear,clc,close all;
Image=rgb2gray(imread('lotus1.jpg'));
figure,imshow(Image),title('原始图像');
hist=imhist(Image);
bottom=min(Image(:))+1;
top=max(Image(:))+1; 
C=double(top-bottom);
S=zeros(256,1);
J=10^10;
for t=bottom+1:top-1
    miuo=0;
    for j=bottom:t
        miuo=miuo+hist(j)*double(j);
    end
    pixelnum=sum(hist(bottom:t));
    miuo=miuo/pixelnum;
    for j=bottom:t
        miuf=1/(1+abs(double(j)-miuo)/C);
        S(j)=-miuf*log(miuf)-(1-miuf)*log(1-miuf);
    end
        
    miub=0;
    for j=t+1:top
        miub=miub+hist(j)*double(j);
    end
    pixelnum=sum(hist(t+1:top));
    miub=miub/pixelnum;
    for j=t+1:top
        miuf=1/(1+abs(double(j)-miub)/C);
        S(j)=-miuf*log(miuf)-(1-miuf)*log(1-miuf);
    end
    currentJ=sum(hist(bottom:top).*S(bottom:top));
    if currentJ<J
        J=currentJ;
        thresh=t;
    end           
end
result=zeros(size(Image));
result(Image>thresh)=1;
figure,imshow(result);

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

def fuzzy_threshold_segmentation(image):
    image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    hist = cv2.calcHist([image_gray], [0], None, [256], [0, 256])
    bottom = np.min(image_gray) + 1
    top = np.max(image_gray) + 1
    C = float(top - bottom)
    S = np.zeros(256)
    J = 10**10
    for t in range(int(bottom + 1), int(top)):
        miuo = 0
        for j in range(int(bottom), int(t)):
            miuo += hist[j] * float(j)
        pixelnum = np.sum(hist[int(bottom):int(t)])
        miuo = miuo / pixelnum
        for j in range(int(bottom), int(t)):
            miuf = 1 / (1 + abs(float(j) - miuo) / C)
            S[j] = -miuf * np.log(miuf) - (1 - miuf) * np.log(1 - miuf)

        miub = 0
        for j in range(int(t + 1), int(top)):
            miub += hist[j] * float(j)
        pixelnum = np.sum(hist[int(t + 1):int(top)])
        miub = miub / pixelnum
        for j in range(int(t + 1), int(top)):
            miuf = 1 / (1 + abs(float(j) - miub) / C)
            S[j] = -miuf * np.log(miuf) - (1 - miuf) * np.log(1 - miuf)

        currentJ = np.sum(hist[int(bottom):int(top)] * S[int(bottom):int(top)])
        if currentJ < J:
            J = currentJ
            thresh = t

    result = np.zeros_like(image_gray)
    result[image_gray > thresh] = 255
    return result

if __name__ == "__main__":
    image = cv2.imread('lotus1.jpg')
    segmented_image = fuzzy_threshold_segmentation(image)

    plt.figure()
    plt.subplot(1, 2, 1)
    plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
    plt.title('原始图像')
    plt.subplot(1, 2, 2)
    plt.imshow(segmented_image, cmap='gray')
    plt.title('分割结果')
    plt.show()

三：边界分割

（1）基于梯度的边界闭合

基于梯度的边界闭合：是一种图像边界分割技术，旨在从图像中找到封闭的边界或物体轮廓。该方法利用图像梯度信息来检测边缘，并通过将边缘点连接起来形成封闭的轮廓。基本步骤如下

计算图像梯度：首先，通过应用梯度算子（如Sobel、Prewitt、或Canny算子）计算图像的梯度。梯度表示图像中灰度值变化的强度和方向
边缘检测：根据梯度计算结果，选择一个适当的阈值来检测图像中的边缘。可以使用阈值化方法（如固定阈值或自适应阈值）来将梯度图像转换为二值图像，其中边缘点被设置为白色，非边缘点被设置为黑色
边缘连接：在边缘检测后，可能会存在一些不完整的边缘线段。为了得到封闭的轮廓，需要将边缘点连接起来。这可以通过应用边缘跟踪算法（如霍夫变换或其他边缘追踪方法）来实现。边缘跟踪算法可以找到相邻的边缘点并将它们连接成连续的边缘线
边缘闭合：边缘连接后，通常会得到一个未完全封闭的边界。为了使边界封闭，可以使用形态学操作（如膨胀、闭操作）来填充边界内的空洞
可选的后处理：根据应用需求，可以进行一些后处理步骤，如去除小的噪声区域、平滑边界线等

（2）霍夫（Hough）变换

霍夫（Hough）变换：是一种在图像处理和计算机视觉领域中广泛使用的技术。它最初是由霍夫（Hough）于1962年提出，用于检测图像中的直线，但后来被扩展用于检测其他形状，如圆、椭圆等。霍夫变换主要用于在图像中检测几何形状，并且对噪声和不完整形状边缘具有较好的鲁棒性。核心思想是建立一种点-线对偶关系，将图像从图像空间变换到参数空间，确定曲线的参数，进而确定图像中的曲线。若边界线形状已知，通过检测图像中离散的边界点，确定曲线参数，在图像空间重绘边界曲线，进而改良边界。步骤如下

边缘检测：首先，需要对图像进行边缘检测，以便在霍夫变换中处理边缘点。可以使用Canny边缘检测等方法来获取图像的边缘
参数空间表示：对于待检测的几何形状（如直线），需要选择适当的参数表示。例如，对于直线，通常使用极坐标（ρ, θ）来表示，其中ρ表示从原点到直线的垂直距离，θ表示直线的倾斜角度
累加器数组：创建一个累加器数组，在参数空间中为每个可能的参数组合（ρ, θ）初始化计数为0
投票过程：对于边缘图像中的每个边缘点，根据其在参数空间中的可能参数（ρ, θ）对累加器数组进行投票，即将对应的计数值加一
阈值设定：根据累加器数组中的投票结果，可以设置一个阈值，用于确定检测到的几何形状。只有当累加器数组中的计数值大于设定的阈值时，才被视为有效的几何形状
参数反变换：根据累加器数组中的有效投票，将参数反变换回原始图像空间，得到检测到的几何形状在图像中的位置

霍夫变换在图像中检测直线、圆、椭圆等形状方面具有很强的鲁棒性和广泛的应用。然而，霍夫变换的计算复杂度较高，对于大规模图像或复杂形状的检测可能需要较多的计算资源。因此，在实际应用中，可以根据具体情况选择使用霍夫变换或其他更高效的方法来检测几何形状

如下

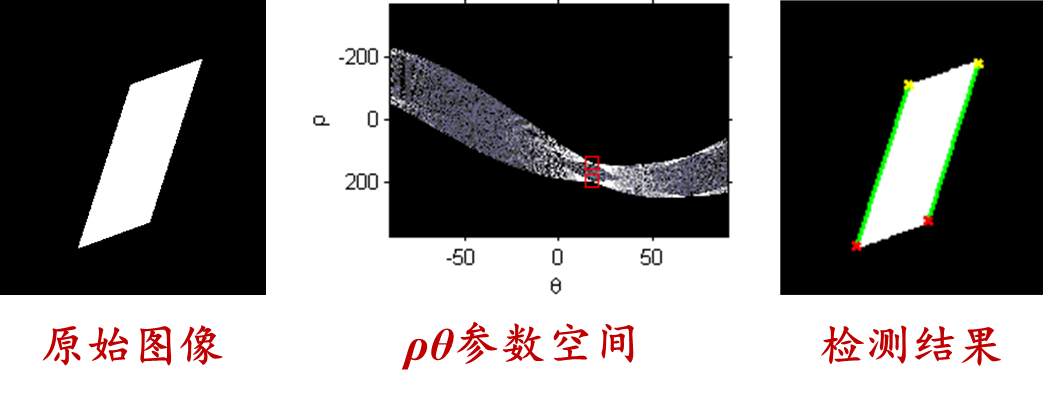
在这里插入图片描述

matlab实现：

Image=rgb2gray(imread('houghsource.bmp'));
bw=edge(Image,'canny');
figure,imshow(bw);
[h,t,r]=hough(bw,'RhoResolution',0.5,'ThetaResolution',0.5);
figure,imshow(imadjust(mat2gray(h)),'XData',t,'YData',r,'InitialMagnification','fit');
xlabel('\theta'),ylabel('\rho');
axis on,axis normal,hold on;
P=houghpeaks(h,2);
x=t(P(:,2));
y=r(P(:,1));
plot(x,y,'s','color','r');
lines=houghlines(bw,t,r,P,'FillGap',5,'Minlength',7);
figure,imshow(Image);
hold on;
max_len=0;
for i=1:length(lines)
    xy=[lines(i).point1;lines(i).point2];
    plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','g');
    plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','y');
    plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','r');
end

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为灰度图像
image = cv2.imread('houghsource.bmp')
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 边缘检测
bw = cv2.Canny(image_gray, 100, 200)

# 显示边缘图像
plt.figure()
plt.imshow(bw, cmap='gray')
plt.title('边缘图像')
plt.show()

# Hough变换
h, t, r = cv2.HoughLines(bw, rho=0.5, theta=np.pi/360, threshold=100)

# 显示Hough变换结果
plt.figure()
plt.imshow(np.log(1 + h), extent=[np.rad2deg(t[-1]), np.rad2deg(t[0]), r[-1], r[0]],
           cmap='gray', aspect=1/2)
plt.title('Hough变换结果')
plt.xlabel('Theta (degrees)')
plt.ylabel('Rho')
plt.show()

# 提取Hough变换的峰值点
P = cv2.HoughPeaks(h, 2, np.pi/360, threshold=100)

# 显示提取的峰值点
plt.figure()
plt.imshow(np.log(1 + h), extent=[np.rad2deg(t[-1]), np.rad2deg(t[0]), r[-1], r[0]],
           cmap='gray', aspect=1/2)
plt.title('Hough变换结果（峰值点）')
plt.xlabel('Theta (degrees)')
plt.ylabel('Rho')
plt.plot(np.rad2deg(t[P[:, 1]]), r[P[:, 0]], 's', color='r')
plt.show()

# 提取直线并在原图上绘制
lines = cv2.HoughLinesP(bw, 1, np.pi/180, threshold=100, minLineLength=7, maxLineGap=5)

plt.figure()
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('检测到的直线')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0, image.shape[1])
plt.ylim(image.shape[0], 0)

for line in lines:
    x1, y1, x2, y2 = line[0]
    plt.plot([x1, x2], [y1, y2], 'g-', linewidth=2)
    plt.plot(x1, y1, 'yx', markersize=8)
    plt.plot(x2, y2, 'rx', markersize=8)

plt.show()

（3）边界跟踪

边界跟踪：是一种在图像处理和计算机视觉中用于提取物体轮廓的技术。边界跟踪的目标是找到物体在图像中的边界像素，从而得到物体的轮廓信息。边界跟踪算法通常从一个起始点开始，沿着物体的边界像素依次进行跟踪，直到回到起始点为止。跟踪过程根据像素的连通性进行，从当前像素找到下一个相邻的边界像素，然后跳转到该像素进行跟踪，直到回到起始点为止。以下是一种简单的边界跟踪算法（8邻域跟踪算法）的基本步骤

选择起始点：选择一个图像中的像素点作为起始点，该点应该位于物体边界上
8邻域搜索：从起始点开始，按照8邻域的方式搜索相邻像素。对于当前像素，检查其8个相邻像素（上、下、左、右、左上、右上、左下、右下），找到第一个边界像素（通常为非背景像素），然后将当前像素更新为该边界像素，并将该边界像素添加到边界点集合中
继续跟踪：重复步骤2，直到回到起始点
停止跟踪：当回到起始点时，边界跟踪结束，此时边界点集合中存储的像素就是物体的轮廓信息

边界跟踪算法可以用于物体检测、图像分割、轮廓提取等应用。不同的边界跟踪算法有不同的连通性要求和终止条件，常见的边界跟踪算法还包括4邻域跟踪算法和Moore-Neighbor跟踪算法等。在实际应用中，可以根据图像的特点和应用需求选择合适的边界跟踪算法

如下

在这里插入图片描述

matlab实现：

Image=im2bw(imread('algae.jpg'));
Image=1-Image;                      %bwboundaries函数以白色区域为目标，本图中目标暗，因此反色。
[B,L]=bwboundaries(Image);
figure,imshow(L),title('划分的区域');
hold on;
for i=1:length(B)
    boundary=B{i};
    plot(boundary(:,2),boundary(:,1),'r','LineWidth',2);
end

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为二值图像
image = cv2.imread('algae.jpg')
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
_, Image = cv2.threshold(image_gray, 128, 255, cv2.THRESH_BINARY)

# 反色处理
Image = 255 - Image

# 使用cv2.findContours函数获取边界点
contours, _ = cv2.findContours(Image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

# 绘制边界
plt.figure()
plt.imshow(Image, cmap='gray')
plt.title('划分的区域')
plt.xlabel('x')
plt.ylabel('y')

for contour in contours:
    contour = contour.squeeze()
    plt.plot(contour[:, 1], contour[:, 0], 'r', linewidth=2)

plt.show()