1、草药迷阵问题

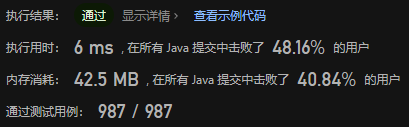
\qquad 有一个10*10的百草药柜，每一个抽屉里都有5种不同属性的草药，依次打开抽屉来长出草药迷阵，要求寻找一种神奇的药方，满足：

• 横行：每一种被选取的草药都要和相邻的抽屉里选的草药相互符合相生相克的关系
• (1,1) 不能从抽屉里选取金属性的草药
• 纵列：最少一种，最多两种金属性和土属性的草药

2、时序回溯搜索

\qquad 首先列举可能的选择来做决策：
\qquad \qquad - 选择一个决策
\qquad \qquad - 在所有现有的可能性里面选择一个，且保证这个选择跟目前为止已做的决策是“兼容的”
\qquad \qquad - 如果当前的选择与某些约束冲突了，考虑另一个可行的选择
\qquad 如果所有的决策都互相兼容，那么我们就找到一个解
\qquad 如果在任意一个步骤，没有任何可行的选择作为决策，则修改上一个决策
\qquad 时序回溯搜索其实是一个搜索树的搜索过程，其示意如下图所示：

\qquad 为了更好地程序化时序回溯搜索算法，首先做出下述定义，令$fix(D)$表示一个变量的集合，其中的所有变量$X$都已经被赋予一个数值，称$fix(D)$中的变量为已经被固定的变量；令$satisfied(c)$表示一个函数，用于检查某一条约束$c$的变量是否都已经被固定了。令$check(C,D)$表示一个函数，用于检查约束集合$C$中的所有约束的值域。

 check(C,D):
 	foreach c in C:
 		if(vars(c) in fixed(D)):
 			if not satisfied(c) return false domain #约束c中不是所有变量均已被固定
 	return D 									#约束c中所有变量均已被固定

\qquad 基本回溯搜索算法的流程如下所示：

back_search(C,D):
	if(vars(C) in fixed(D)) return check(C,D)
	X = choose(vars(C)-fixed(D))#选择下一个尝试固定的变量
	foreach d in D(X):
		D1 = check(C and {X=d}, D)
		if(D1=D):
			D2 = back_search(C and {x=d}, D)
			if(D2 is not a false domain) return D2
	return false domain

\qquad 在搜索里，变量的顺序(choose())的影响十分大，不同的选择直接影响到搜索树的大小的搜索效率；
\qquad 函数$choose()$允许采用不同的方法选择下一个变量，最简单的方法是根据他们的输入顺序依次进行选择；也可以基于其他规则进行选取，如根据变量值域的大小，选择值域最大或者最小的变量。
\qquad 在对某个变量的值域进行搜索时，i.e., foreach d in D(X)，搜索的顺序会影响到搜索的效率，好的选择可以使得可行解更早地被找到，从而加速剪枝和缩短求解时间。

3、传播+搜索

\qquad 约束传播是一个有效且高效的推理方式，可以从变量的值域中移除那些确保不会出现在解中的数值，从而可以得到更小的值域和更小的搜索树。
\qquad 应用约束+传播的思路为：在每一个搜索节点上，在枚举搜索下一个变量之前，进行约束传播。
\qquad 将约束传播技术融入到搜索过程，得到的强化版本的搜索-传播算法如下所示：

prop_search(F0,Fn,D):
	D = isolv(F0,Fn,D) #通过约束传播更新值域
	if(D is a false domain) or (all X: |D(X)| =1):
		return D
	X = choose(vars(C))
	foreach d in D(X):
		D1 = back_search(F0 and Fn, {prop(X=d)}, D)
		if(D1 is not a false domain) return D1
	return false domain

\qquad 使用二叉分枝的方法如下所示：

\qquad 上述二叉分枝中，$choose(D)$函数用于将父结点划分成两个子结点，其中的划分方法可以有如下几种，首先选择一个变量$X$，其值域中的值的个数$|D(X)|>1$，在其值域中选择一个值$d\in D(X)$。第一种方法是：在一个分枝中令 $X=d$，在另一个分枝结点中令$X\ne d$。另外一种分枝方法是：在一个分枝中令$X\le d$，在另一个分枝中令$X\ge d+1$。上述分枝方法在约束传播中叫做值域分割。

THE END