一.复制带有随机指针的链表

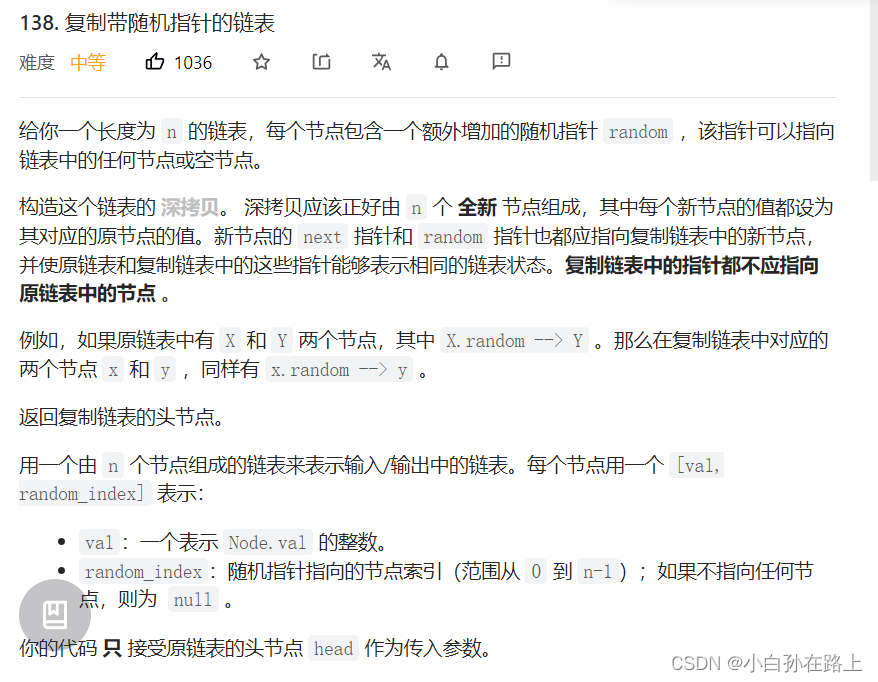
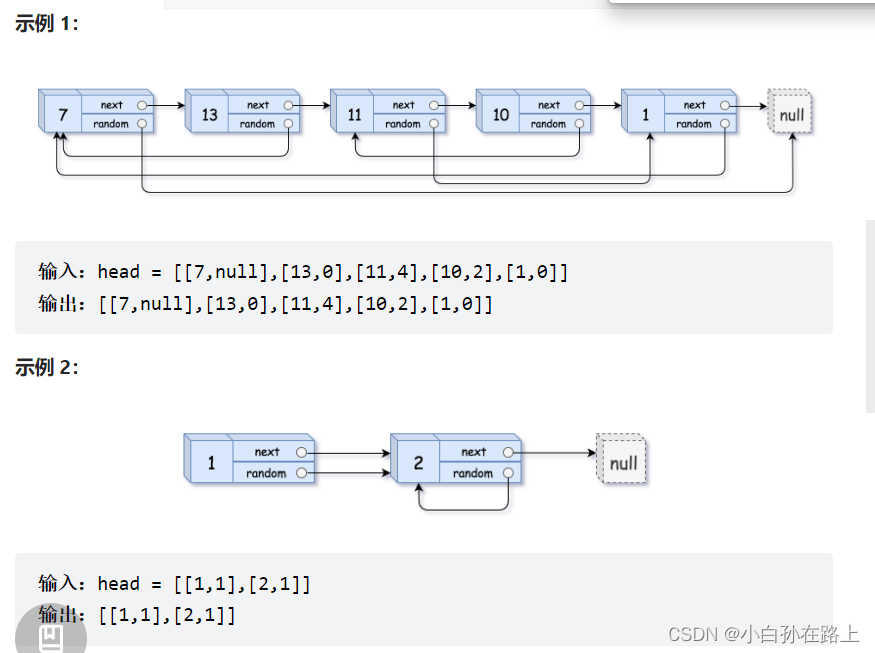
要求结构和val都是一样

这个题目我们可以建立一个map表,把新的链表和旧的链表每个节点都构成一组key-val对应

然后遍历旧链表.找到对应的next值和random'值

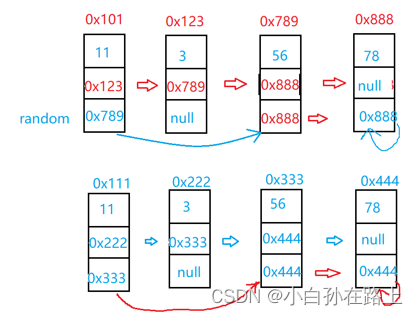
思路:

方法1:迭代+map

class Solution { public Node copyRandomList(Node head) { if(head==null) return null; Node cur =head;//建立一个先驱节点遍历链表 Map<Node,Node> map=new HashMap<>(); while(cur!=null){ Node node=new Node(cur.val); map.put(cur,node);//放到map表里 cur=cur.next; } cur=head; while(cur!=null){ map.get(cur).next=map.get(cur.next); map.get(cur).random=map.get(cur.random); cur=cur.next; } return map.get(head); } }

方法二 递归

将hash表放在外,防止每次递归都改变表,

每次递归前看是否有head.表里没有就直接返回head对应的headNEW的值

如果没有,就建立对应的节点

并把对应的kv放进去

新的节点的下一个和随机值都进入下一个递归.

class Solution { Map<Node,Node> map=new HashMap<>(); public Node copyRandomList(Node head) { if(head==null) return null; while(!map.containsKey(head)){ Node headNew=new Node(head.val); map.put(head,headNew); headNew.next=copyRandomList(head.next); headNew.random=copyRandomList(head.random); } return map.get(head); } }

复杂度分析

时间复杂度：O(n)O(n)，其中 nn 是链表的长度。对于每个节点，我们至多访问其「后继节点」和「随机指针指向的节点」各一次，均摊每个点至多被访问两次。

空间复杂度：O(n)O(n)，其中 nn 是链表的长度。为哈希表的空间开销。

方法3直接复制

思路:新节点接在老节点之后，连接新随机指针，分离链表

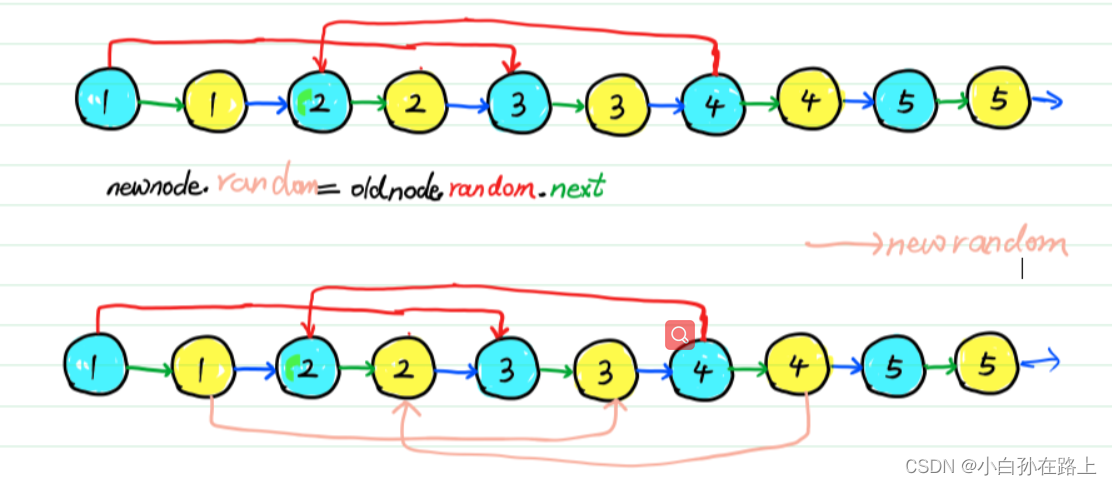
这里解释如何复制的步骤。 图中，黄色为新节点，蓝色为老节点。

1：原始链表，含随机指针，这里仅显示两个，画多了自己看着也乱。

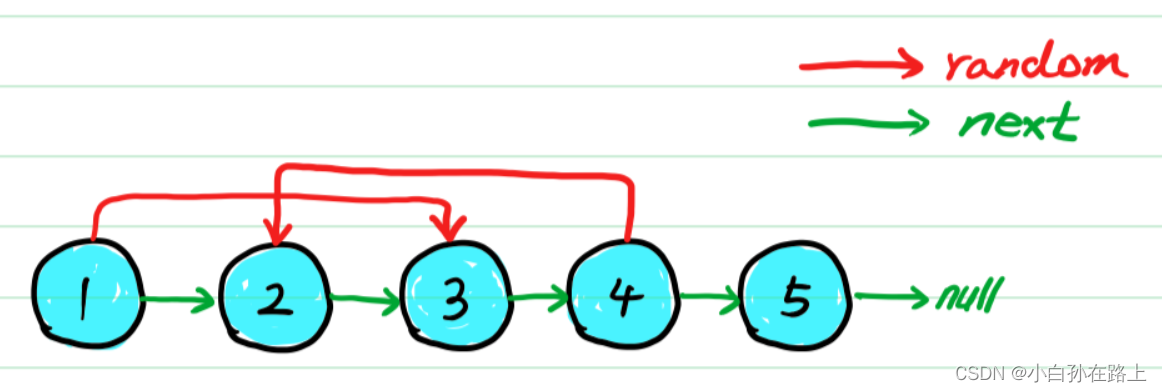
2.2：在每一个老节点之后，新建与老节点val相同的节点，插入在老节点之后，注意，随机指针不急赋值，因为随机在何处还不知，需要把链表全部新老节点建立连接完成。

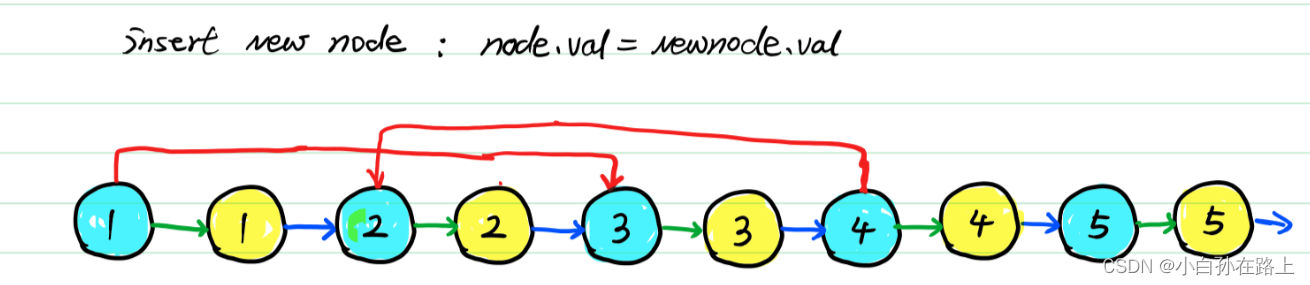
3：赋值新随机指针，等于为老随机指针的下一个。

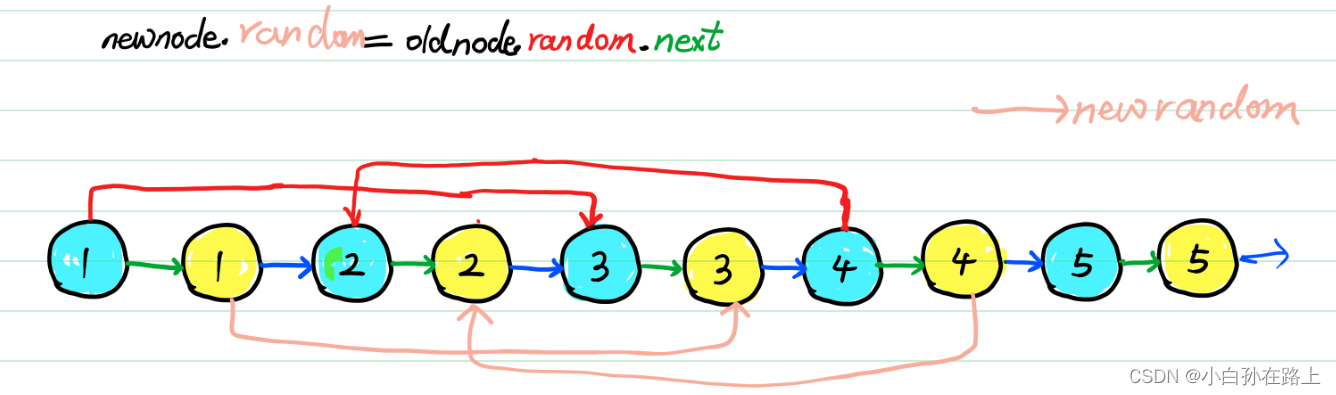
4：拆分链表。随机指针不受影响，老链表依然在，新链表复制完成

5：最后结果

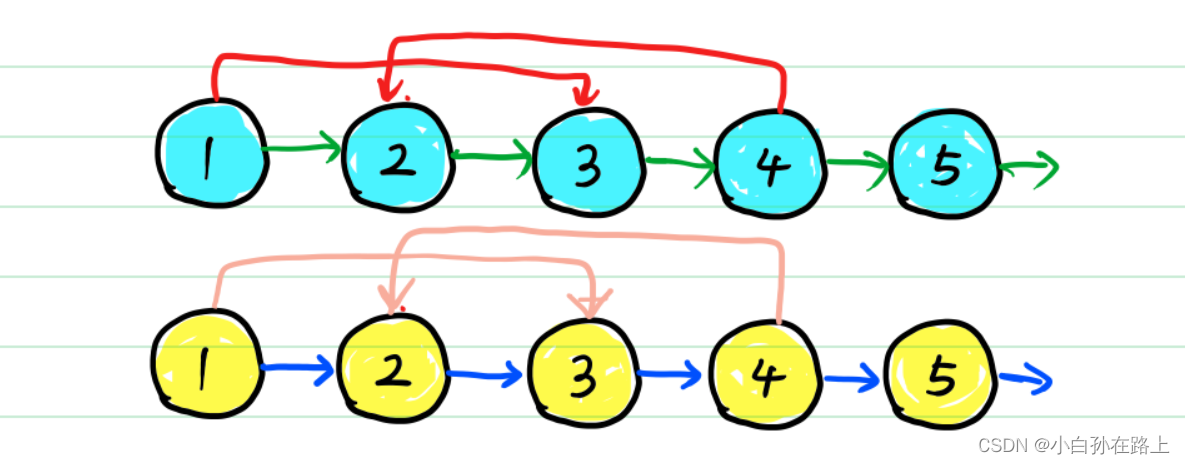
class Solution { public Node copyRandomList(Node head) { if(head==null) return null; Node pHead=head;//建立指针 连接链表 while(pHead!=null){ Node copyNode=new Node(pHead.val); copyNode.next=pHead.next; pHead.next=copyNode; pHead=pHead.next.next; } //建立随机指针 pHead=head; Node randompHead=pHead.next;//对应新节点的位置,为什么定义在外面,因为最后一个节点一定遍历不到(链表总数是偶数),需要额外遍历 while(randompHead.next!=null){ if(pHead.random!=null) randompHead.random=pHead.random.next; pHead=pHead.next.next; randompHead=randompHead.next.next; } if(pHead.random!=null){ randompHead.random=pHead.random.next; }//处理最后一个情况; //分离链表 Node pre=new Node(1); Node newHead=pre;//防止后期找不到头结点 pHead=head; while(pHead!=null){ pre.next=pHead.next; pre=pre.next; pHead.next=pre.next;//分离 pHead=pHead.next; } return newHead.next; }

二.宝石与石头

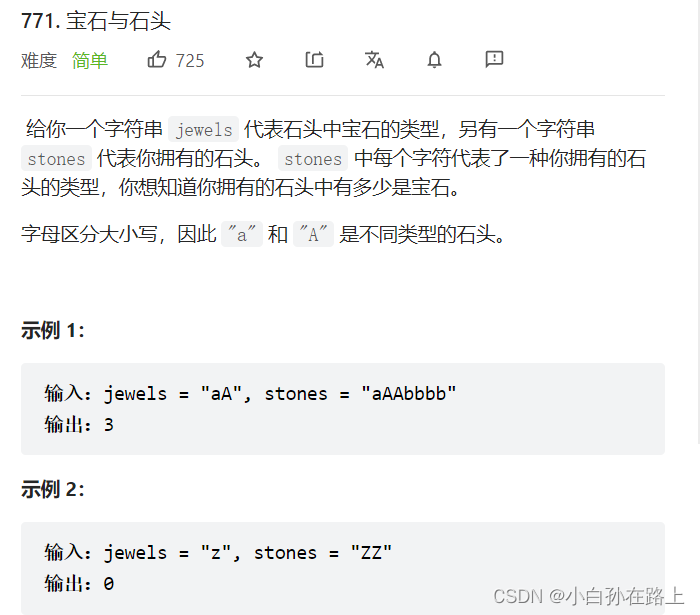
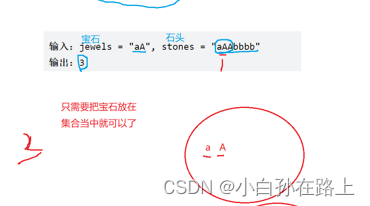
用set做.因为set是一个不重复集合

class Solution { public int numJewelsInStones(String jewels, String stones) { Set<Character> set=new HashSet<>(); for(char s:jewels.toCharArray()){ set.add(s); } int count=0; for(char s:stones.toCharArray()){ if(set.contains(s)){ count++; } } return count; } }

三.坏键盘打字

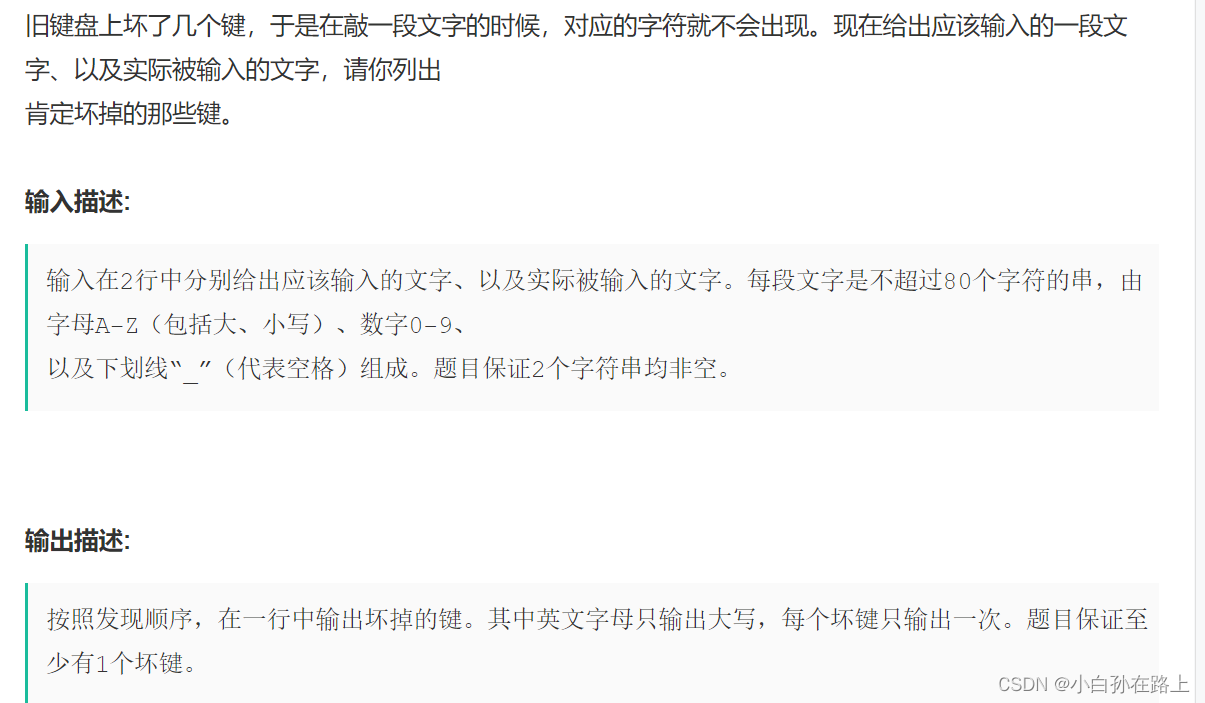
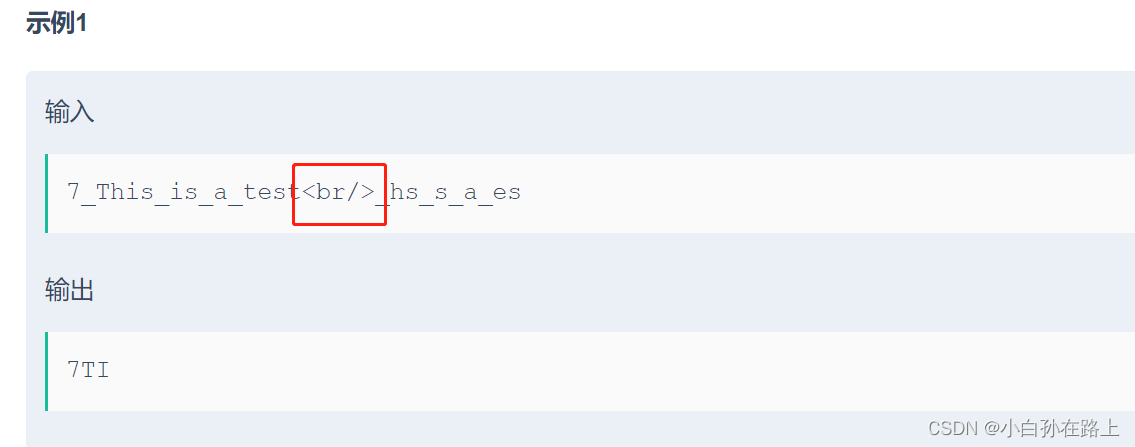
这里的
是前端换行的意思

要求输出大写,且按照发现顺序

观察一下,可以发现没有输出的7ti不管大写小写都没办法输出,就说明我们可以先把变成大写.统一处理

定义两个集合,一个是放在是实际输出的,

还有一个是坏的建.因为可能坏的字母重复出现多次,

并且一旦出现坏的,我们就打印,因为这是一个hashset 顺序不是按照发现顺序来的

方法1 set方法

import java.util.*; public class Main{ public static void main(String[] args){ Scanner sc=new Scanner(System.in); String s1=sc.nextLine();//好的 String s2=sc.nextLine();//实际输出的 Set<Character> badset=new HashSet<>(); Set<Character> goodset=new HashSet<>(); for(char ch:s2.toUpperCase().toCharArray()){ goodset.add(ch); } for(char ch:s1.toUpperCase().toCharArray()){ if(!goodset.contains(ch)&&!badset.contains(ch)){ System.out.print(ch); badset.add(ch); } } } }

方法2 sb做法

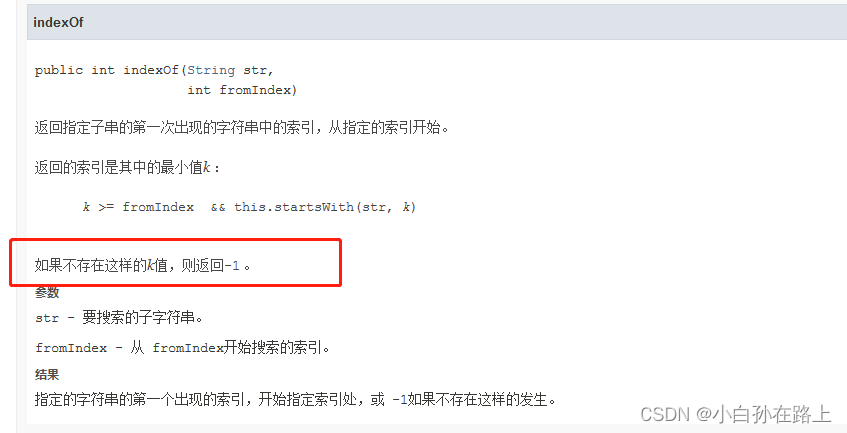
遍历好的 如果有在好的中没有的,或者在sb里也没有的就拼接到sb里

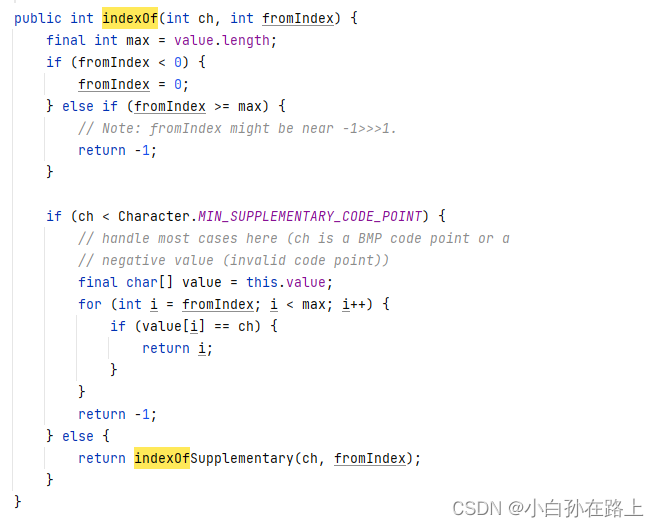
这里注意,sb没有indexof 需要tostring

import java.util.*; public class Main{ public static void main(String[] args){ Scanner sc=new Scanner(System.in); String s1=sc.nextLine().toUpperCase(); String s2=sc.nextLine().toUpperCase(); StringBuilder sb=new StringBuilder(); // char[] ch1=s1.toUpperCase().toCharArray(); // char[] ch2=s2.toUpperCase().toCharArray(); for(int i=0;i<s1.length();i++){ if(s2.indexOf(s1.charAt(i))==-1&&sb.toString().indexOf(s1.charAt(i))==-1){ System.out.print(s1.charAt(i)); sb.append(s1.charAt(i)); } } } }

方法三 map法

yuset法大同小异

public class B1019OldKeyboard { public static void main(String[] args) { Scanner sc = new Scanner(System.in); String old = sc.next(); String result = sc.next(); Map<Character, Integer> mapResult = new HashMap<>(); Map<Character, Integer> mapOld = new HashMap<>(); char[] charsResult = result.toUpperCase().toCharArray(); char[] charsOld = old.toUpperCase().toCharArray(); for (int i = 0; i < charsResult.length; i++) { if (!mapResult.containsKey(charsResult[i])) { mapResult.put(charsResult[i], i); } } List<Character> list = new ArrayList<>(); for (int i = 0; i < charsOld.length; i++) { if (!mapResult.containsKey(charsOld[i])) { if (!mapOld.containsKey(charsOld[i])) { mapOld.put(charsOld[i], i); list.add(charsOld[i]); } } } for (int i = 0; i < list.size(); i++) { System.out.print(list.get(i)); } } }

四.前k个高频单词

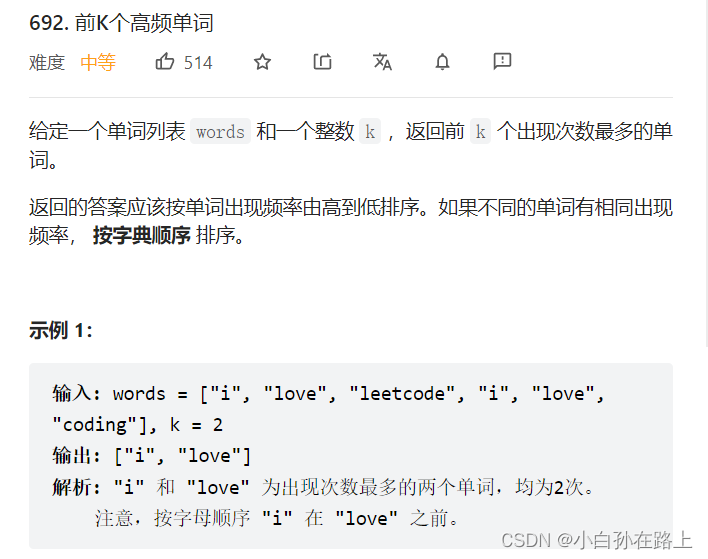
这题的思路就是遍历字符数组,建立一个map表,把对应的单词和对应的频率放在堆里

怎么样存储k-v

就要用

他也属于一个类,

因为我们是小根堆,但是这里有两个值,我们需要new一个comparator

我们来自己指定是key还是value很显然是频率

然后遍历map

用foreach循环

小于k的时候就把map的值放进去

大于map的时候,

就看堆顶元素是否小于entry.是就弹出来,让entry放进去

这样写当然错了.要看对应的频率

这里还是错了.我们要先判断相同的情况,

这里错了,Integer是引用类型不能用==比较

然后频率相同我们比较单词大小

频率不同我们找频率大的

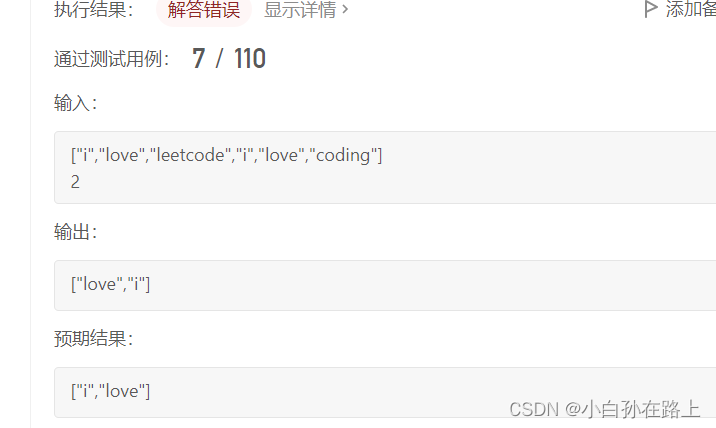
到这里我们发现出现了错误,我们弹出的结果没有逆置.所以应该要把list逆置一下

只要用集合的工具类就行

这里发现测试用例虽然通过多了

还是出现了问题

我们分析一下

这里可能我们放了三个,就没进行,后面的交换,直接跳出循环,遍历完map表了

那么我们会发现,问题出现在了这里

你小于k的时候,你就直接放入

根据这个比较方法比较

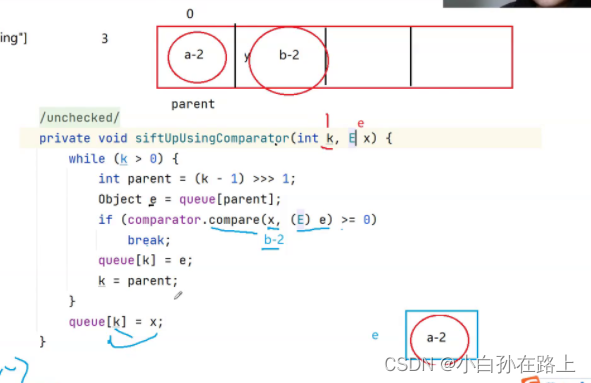
这样是没问题的,但是后续又逆置,把逆置回来了.

没有按照字母排序

解决方法

就是要让字母大的放在堆顶.结束的时候逆置就变成正的了

所以我们需要改变一下比较方法

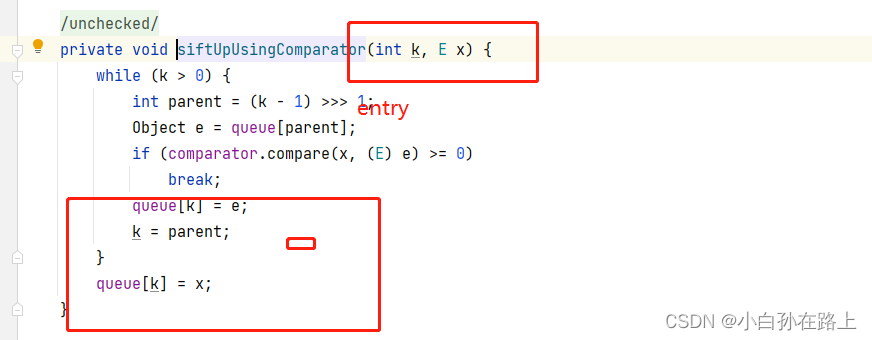
class Solution { public List<String> topKFrequent(String[] words, int k) { //1.统计每个单词出现的次数用map Map<String,Integer> map=new HashMap<>(); for (String s:words) { if(!map.containsKey(s)){ map.put(s,1); }else{ int freq=map.get(s); map.put(s,freq+1); } } //2.建立一个大小为k的小根堆 PriorityQueue<Map.Entry<String,Integer>> minHeap=new PriorityQueue<>(k, new Comparator<Map.Entry<String, Integer>>() { @Override public int compare(Map.Entry<String, Integer> o1, Map.Entry<String, Integer> o2) { if(o1.getValue().compareTo(o2.getValue())==0){ return o2.getKey().compareTo(o1.getKey());//根据字符串比较的大根堆 } return o1.getValue()-o2.getValue();//根据频率比较 } }); //3.遍历map表 for(Map.Entry<String,Integer> entry:map.entrySet()){ if(minHeap.size()<k){ minHeap.offer(entry); }else{ Map.Entry<String,Integer> top=minHeap.peek(); if(top.getValue().compareTo(entry.getValue())==0){ if(top.getKey().compareTo(entry.getKey())>0){//entry的单词更小 minHeap.poll(); minHeap.offer(entry); } }else{ if(top.getValue().compareTo(entry.getValue())<0){ minHeap.poll(); minHeap.offer(entry); } } } } List<String> list=new ArrayList<>(); while(!minHeap.isEmpty()){ Map.Entry<String,Integer> top=minHeap.poll(); list.add(top.getKey()); } Collections.reverse(list); return list; } }

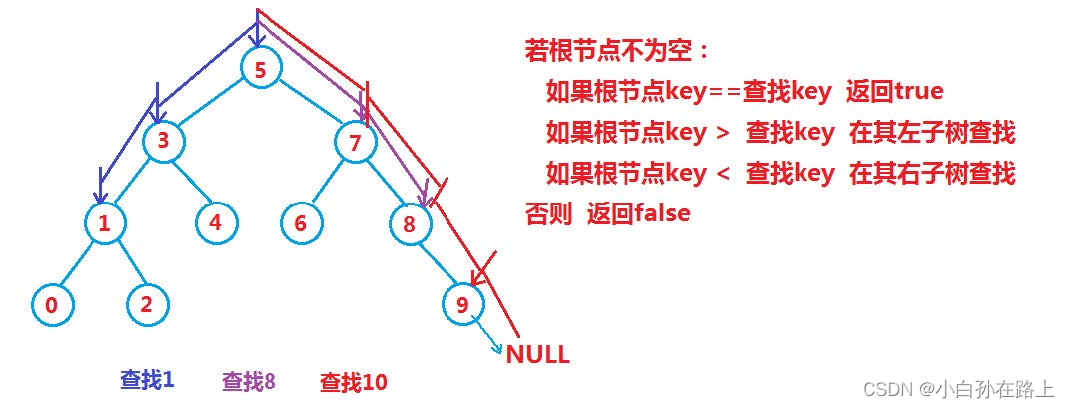
五.二叉搜索树

1 概念

二叉搜索树又称二叉排序树，它或者是一棵空树**，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

它的左右子树也分别为二叉搜索树

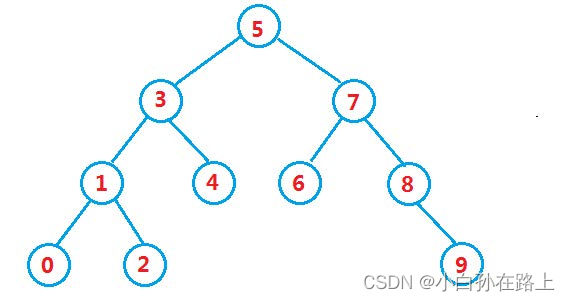
int a [] = {5,3,4,1,7,8,2,6,0,9};

2 操作-查找