浮点数的存储

news2024/9/22 5:28:21

❤️ 作者简介：对纯音乐情有独钟的阿甘致力于C、C++、数据结构、TCP/IP、数据库等等一系列知识，对纯音乐有独特的喜爱
📗 日后方向 : 偏向于CPP开发以及大数据方向，如果你也感兴趣的话欢迎关注博主，期待更新

1. 浮点型在内存中的存储

常见的浮点数：
3.14159
1E10 -->1.0乘10的十次方
浮点数家族包括： float、double、long double 类型。

1.1 一个例子

浮点数存储的例子：
在这里插入图片描述

我们来思考一下，我们printf出来的值到底是什么呢？
我们将n的地址强转成float的类型给pfloat接收，我们再用%f来输出出来
用pfloat接收9.0在用%f输出。

接下来我们来看输出情况：
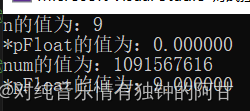
在这里插入图片描述

这个结果与你心中的结果是否一致呢？
为什么*pfloat输出出来不是9.00000呢？
我们会发现，他们存储方式是不是不一样呢？
接下来让我们来了解浮点数的存储规则

1.2浮点数存储规则

num 和 *pFloat 在内存中明明是同一个数，为什么浮点数和整数的解读结果会差别这么大？
要理解这个结果，一定要搞懂浮点数在计算机内部的表示方法。
详细解读：
根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：
(-1)^S * M * 2^E
(-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
M表示有效数字，大于等于1，小于2。
2^E表示指数位。

举例来说：
十进制的5.0，写成二进制是 101.0 ，相当于 1.01×2^2 。
那么，按照上面V的格式，可以得出S=0，M=1.01，E=2。
十进制的-5.0，写成二进制是 -101.0 ，相当于 -1.01×2^2 。那么，S=1，M=1.01，E=2。
IEEE 754规定：
对于32位的浮点数，也就是float(4个字节–32比特位)，最高的1位是符号位S，接着的8位是指数E，剩下的23位为有效数字M。
在这里插入图片描述

对于64位的浮点数，也就是double（8个字节–64个比特位）最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。
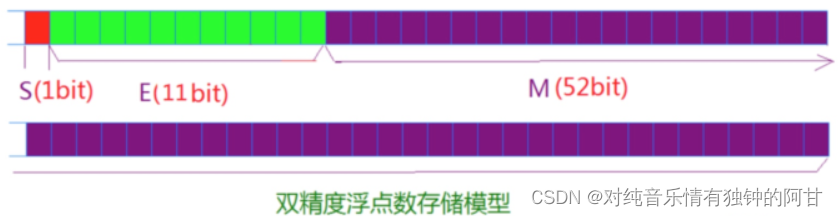
在这里插入图片描述

IEEE 754对有效数字M和指数E，还有一些特别规定。
前面说过， 1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。
IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的
xxxxxx部分。比如保存1.01的时
候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位
浮点数为例，留给M只有23位，
将第一位的1舍去以后，等于可以保存24位有效数字。
至于指数E，情况就比较复杂。
首先，E为一个无符号整数（unsigned int）
这意味着，如果E为8位，它的取值范围为0_{255；如果E为11位，它的取值范围为0}2047。但是，我们
知道，科学计数法中的E是可以出
现负数的，所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数
是127；对于11位的E，这个中间
数是1023。比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即
10001001。

然后，指数E从内存中取出还可以再分成三种情况：

E不全为0或不全为1

这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将
有效数字M前加上第一位的1。
比如：
0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为
1.0*2^(-1)，其阶码为-1+127=126，表示为
01111110，而尾数1.0去掉整数部分为0，补齐0到23位00000000000000000000000，则其二进
制表示形式为:
0 01111110 00000000000000000000000