大家好,我们接第二部分继续分析金融数据。
配对图和相关矩阵
证券中的相关性分析为我们提供了有趣的投资策略。市场中一个广为人知的策略叫做“Long-Short”,即买入一家公司的证券,同时卖出另一家公司的证券,相信这两个资产在市场上有相反的趋势。也就是说,当一个股票上涨时,另一个就会下跌。为了制定Long-Short策略,投资者依赖于证券之间的相关性分析。
相关性分析不仅对Long-Short策略有用,而且对于避免系统性风险也非常关键,系统性风险是指整个系统崩溃的风险,而不仅仅是个别部分的失败。简单来说,如果你的投资组合中的证券高度相关,或者都在同一行业,如果发生了特定行业的问题,所有证券都可能失去市场价值,导致更大的经济损失。
配对图和相关矩阵是可视化资产之间相关性的有用工具。在相关矩阵中,数值范围在-1和1之间,其中-1表示完全负相关,1表示完全正相关。请记住,当资产呈正相关时,它们往往同时在市场上上涨和下跌,而当资产呈负相关时,则相反。
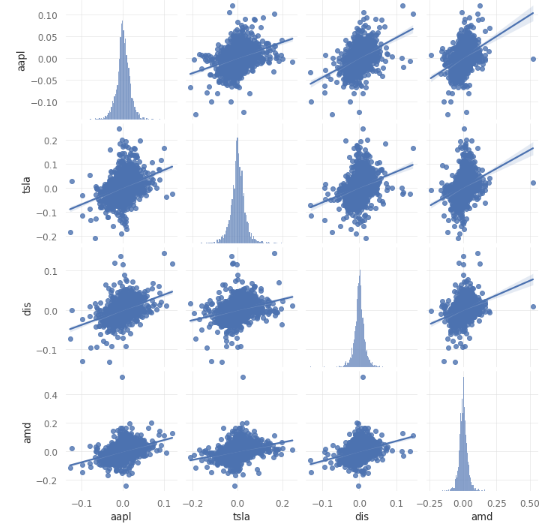
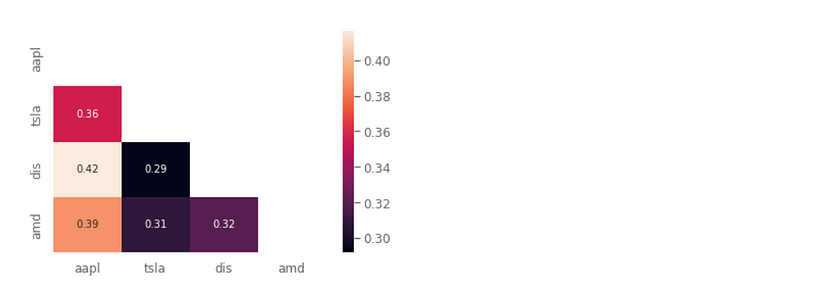
需要注意的是,以上资产之间没有负相关,这表明它们之间没有任何一个可以限制损失。在金融市场中,对冲是一种投资头寸,旨在通过投资与投资组合中其他资产可能存在负相关的资产来抵消潜在的损失。许多投资者购买黄金来作为对风险更高的投资的保护,当整个市场进入熊市时,黄金往往会增值,从而限制潜在损失。
Beta和Alpha
Beta和Alpha是金融领域中用于评估证券相对于整个市场表现的两个关键指标。Beta是一个证券相对于市场波动性的度量,Beta为1表示该证券的波动性与市场一样,大于1的Beta表示其比市场更具波动性,而小于1的Beta则表示其波动性较低。
另一方面,Alpha是证券超额收益相对于基于其Beta的预期表现的度量。正的Alpha表示该证券在基于其Beta的预期表现方面表现优异,而负的Alpha则表明表现不佳。通过分析证券的Beta值和Alpha值,投资者可以更好地了解该证券与市场相比的风险和潜在回报,并相应地做出明智的投资决策。
要确定Beta和Alpha,我们需要来自SP500指数的数据作为基准,拟合证券和指数之间的线性回归模型,这将使我们能够提取其Beta和Alpha值。
首先,我们加载SP500指数的数据:
# 从美国的基准指数SP500加载数据
sp500 = qs.utils.download_returns('^GSPC')
sp500 = sp500.loc['2010-07-01':'2023-02-10']
sp500.index = sp500.index.tz_convert(None)接下来,我们可以使用Scikit-Learn线性回归模型来提取Beta和Alpha。
# 拟合苹果公司收益和基准之间的线性关系
X = sp500_no_index.values.reshape(-1,1)
y = aapl_no_index.values.reshape(-1,1)
linreg = LinearRegression().fit(X, y)
beta = linreg.coef_[0]
alpha = linreg.intercept_
print('AAPL beta: ', beta.round(3))
print('\nAAPL alpha: ', alpha.round(3))继续进行相同操作,得到以下结果:
AAPL beta: [1.111]
AAPL alpha: [0.001]
TSLA beta: [1.377]
TSLA alpha: [0.001]
Walt Disney Company beta: [1.024]
Walt Disney Company alpha: [0.0001]
AMD beta: [1.603]
AMD alpha: [0.0006]所有证券的Beta值都大于1,这意味着它们比基准更具波动性,可能提供更高的回报,但也伴随着更高的风险。另一方面,所有证券的Alpha值都很小,接近于零,这表明预期回报和风险调整后的回报之间几乎没有差异。
夏普比率
夏普比率是一种度量投资风险和回报关系的指标。如下图所示:
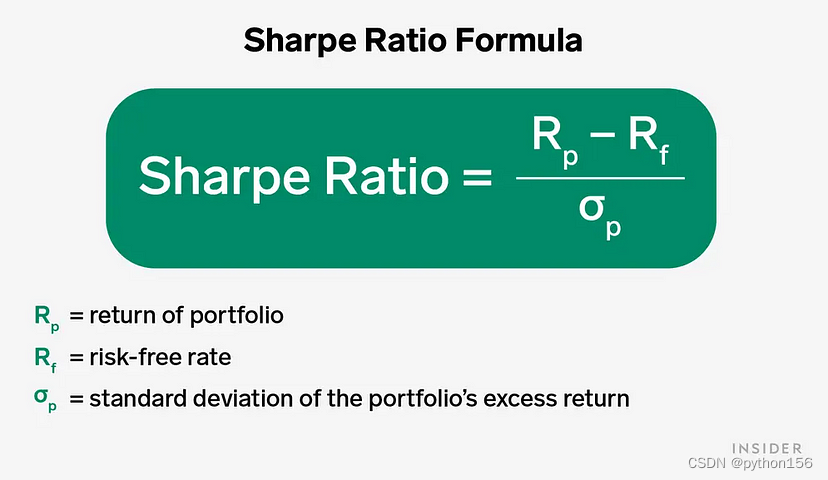
较高的夏普比率表示相对于夏普比率较低的其他投资,该投资提供了更高的回报水平。通常,夏普比率超过1.0被认为是可接受或良好的,2.0或更高被评为非常好,3.0或更高被认为是优秀的。夏普比率为1表示投资的平均回报等于无风险回报率。
使用quantstats,可以获得股票的夏普比率:
# Calculating Sharpe ratio
print("Sharpe Ratio for AAPL: ", qs.stats.sharpe(aapl).round(2))
print("Sharpe Ratio for TSLA: ", qs.stats.sharpe(tsla).round(2))
print("Sharpe Ratio for DIS: ", qs.stats.sharpe(dis).round(2))
print("Sharpe Ratio for AMD: ", qs.stats.sharpe(amd).round(2))Sharpe Ratio for AAPL: 0.97
Sharpe Ratio for TSLA: 0.95
Sharpe Ratio for DIS: 0.55
Sharpe Ratio for AMD: 0.62苹果和特斯拉是分析的数据中夏普比率最高的,分别为0.97和0.95,表明这些投资提供更好的风险回报关系。但是,这些投资的夏普比率都不超过1,这可能表明这些投资的平均回报低于无风险回报率。
总结
通过对以上指标的分析,可以得出以下结论:
-
苹果和特斯拉的夏普比率最好,表明它们具有更好的风险回报关系;
-
特斯拉的回报率是最高的,但其波动性也比苹果和迪士尼更高;
-
与其他资产相比,苹果有更高的回报和低波动性,它具有最佳的夏普比率、低Beta值、低标准差和低回报不对称性;
-
AMD是其中风险更高、波动性更大的投资选项,其回报分布高度不对称,具有高标准差和高Beta值;
-
迪士尼可能是对风险敏感的投资者的不错选择,考虑到它在这段时间内的回报稳定且有规律。
可以说,在分析的资产中,苹果提供了最佳的风险回报关系,具有较高的收益和较低的风险,优于其他选项。