对本文有疑问可以加微信 Tutor_0914联系。也可以访问我的个人辅导网站 :
tutoryou
基本概念
option期权
期权(Option),是一种选择权,指是一种能在未来某特定时间以特定价格买入或卖出一定数量的某种特定商品的权利。 它是在期货的基础上产生的一种金融工具,给予买方(或持有者)购买或出售标的资产(underlying asset)的权利。
期货
期货(Futures)是一种金融衍生品,是指双方在未来的某个时间按照协议约定的价格和时间交换某种标的物的合约。期货合约可以涉及大宗商品(如金属、农产品、能源等)、金融资产(如股票、债券、货币等)以及其他标的物。
期货合约通常包括以下要素:标的物、合约数量、交割时间、交割地点和交割价格等。买方和卖方在签署期货合约时约定了交割时间和交割价格,因此在合约到期时,买方和卖方需要按照约定的价格和时间交换标的物和货款。
期货交易的参与者包括期货交易所、期货经纪公司、期货交易商和投资者等。投资者可以通过买入或卖出期货合约来进行投机或套期保值等操作。期货市场的价格涨跌受多种因素影响,如供求关系、市场预期、政治和经济因素等。
期货市场的主要作用是提供价格发现和风险管理等功能。期货价格可以反映市场对未来供求关系和价格趋势的预期,同时也可以为市场参与者提供一种有效的风险管理工具,帮助他们规避价格波动带来的风险。
实物期权(Real option)
实物期权指的是在进行项目估值时考虑到了商业投资机会的复杂实物项目的期权,这种期权可以在项目寿命期间被行使。使用简单的净现值(NPV)分析可能会导致错误的估值,因为NPV没有考虑到投资选择的灵活性。
净现值(NPV)
净现值(Net Present Value,NPV)是一种金融分析工具,用于计算一个项目或投资的现金流量净值。它的计算基于将未来的现金流量折现到当前的价值。具体地说,NPV计算的是一个项目或投资的未来现金流量与当前的投资成本之间的差异,其中未来的现金流量需要根据预期的利率进行折现。如果项目或投资的NPV为正数,则表明该项目或投资将带来正的净现金流量,因此可以被认为是可行的、有利可图的。如果NPV为负数,则表明该项目或投资将带来负的净现金流量,因此可能是不可行的、亏损的。
通常,NPV用于比较不同项目或投资之间的优劣,以帮助决策者做出最佳的投资决策。在比较中,NPV越高,表明该项目或投资的价值越高。NPV也可以用于评估产品、业务或其他项目的财务可行性,以确定是否值得投资。
无风险折现率(riskless discount rate)
是用于确定投资或估值分析中未来现金流的现值的回报率或折现率。它代表了将来现金流的折现率,以考虑货币的时间价值和与这些现金流相关的风险水平。
无风险折现率通常从市场上的无风险利率中获取,如政府债券收益率或无风险投资的回报率。它被认为是无风险的,因为假设它不承担任何违约或信用风险。
在给定的例子中,无风险折现率被设定为6%。这意味着顾问使用6%的折现率来计算与金矿项目相关的未来现金流的现值。无风险折现率是估值模型中的重要输入,它包括考虑资金的时间价值和风险因素的真实选择和期权定价方法。它有助于确定与不同投资选择相关的现金流的现值,并允许对投资灵活性和实际选择进行适当评估。
风险中性
代表什么意思
Q3
文章以一个具体的案例为例,介绍了如何使用实物期权进行项目估值。案例中,一家政府需要筹集一些资金,雇用一个咨询顾问来确定一个具有100万盎司金储备的黄金矿三年开发许可的正确价值。如果立即开发,该矿产金的总成本为2.9亿美元(这个成本在三年内保持不变)。黄金需要立即出售,但是存储黄金是昂贵的。购买许可的公司将有权在许可期内开发该矿,并不承担任何额外的税收义务。假设黄金的初始价格为每盎司300美元,从历史数据的分析结果中可以得知,黄金价格有65%的概率在一年内上涨20%,有35%的概率下跌20%。无风险折现率为6%,公司可以立即进行开发,或者推迟一年或两年,此后就无法投资了(许可证到期)。政府要求你从公司的角度(不包括许可费,因为其价值尚未确定)产生这个项目的估值。假设公司是无风险偏好的。
在解决这个问题的过程中,你需要使用实物期权定价的方法,计算出各个时间点和状态(如金价上涨还是下跌)下的原子价格,并计算出未来支付的最大价值。文章中提供了一个类似于美式期权定价的图表,用于解释你的推理过程。如果立即开发,该项目的NPV为1000万美元,但因为许可证有效期为三个期间(包括期间0),政府应该收取更高的许可费。
问题的具体要求包括:1. 计算政府应该收取的最高许可费;
3.2
- 为所有未来时间状态计算原子价格,并使用这些价格计算项目的最大价值;
c是不同状态下的各种证券的和,也叫portfolio ,就是资产的配置数量。
Q是矩阵,所有状态下的所有证券的值都有
n是不同证券买的数量
P_s是不容证券下所有状态的和
P_atom是
来自week2的slides
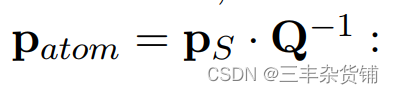
Q是什么


P_atom是什么

- 讨论如果公司是风险厌恶的,原子价格和项目估值会发生什么变化;4. 解释实物期权如何创造价值。
总之,这个问题涉及了金融中实物期权的概念和应用,以及如何使用实物期权定价的方法进行复杂实物项目的估值。
原文
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Copyright c⃝Copyright University of New South Wales 2023. All rights reserved.
Course materials subject to Copyright
UNSW Sydney owns copyright in these materials. The material is subject to copyright
under Australian law and overseas under international treaties. The materials are pro-
vided for use by enrolled UNSW students. The material, or any part derived from this
material, including assignment answers, may not be copied, shared or distributed, in print
or digitally, outside the course without permission. Under no circumstances may these
materials or derived materials be copied or reproduced for sale or commercial purposes
without prior written permission of UNSW Sydney.
WARNING: Your failure to comply with these conditions may lead to disciplinary action,
and may give rise to a civil action or a criminal offence under the law.
THE ABOVE INFORMATION MUST NOT BE REMOVED FROM THIS MATERIAL.
1
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Economics of Finance
Group Assignment
Instruction (Please read carefully.)
This assignment asks you to apply the knowledge gained in classes to analyse practical
questions, present written results in a professional manner, and develop project manage-
ment and teamwork skills. This group assignment should not be left until the last minute.
A suggested time-line is provided below to help to plan your work and writing.
This assignment counts for 20% of the final mark.
The deadline and submission. The deadline for submission of the group assignment is
on Monday, 31 July, 10:00 am. Late submission will incur penalty upto zero
mark. Please submit the assignment in the pdf format through Moodle assignment group
submission in the group assignment folder. The assignment should be typed and nicely
formatted. You can insert Matlab code parts to support your calculation. You may wish
to insert all coding in the Appendix, or integrate in your body text. In any case, you
should mind the logic flow and the readability of your document. Importantly, there are
two other submission components relevant for this assignment: project charter and team
ratings and self-evaluation.
The teamwork and Project Charter. Teamwork is an essential part of the assignment.
The team project charter in the group assignment folder is a project planning and man-
agement tool. Your team will be working together on planning, analysing, developing,
writing up, proofreading and editing your project report ready for submission. You are
also jointly responsible for allocating relevant tasks including research, logistical and or-
ganisational duties. Each team member is expected to have a similar level of involvement
and contribution to the assessment process and product. Each group will need to submit
a charter, signed off (just typed name is sufficient) by each team member. Each group
needs to submit their filled charter, signed by each team member, in the pdf format by
Monday, 17 July, 10:00 am via Moodle submission in the group assignment folder.
Failure to submit Project Charter will result in group mark reduction by 5 marks. If you
are not able to secure signature(s)/agreement(s) of some of the group members, it is fine
to submit a partially signed group charter. One person needs to submit on behalf of the
group.
The team ratings and self-evaluation. After group submission, you will have a chance to
rate your team member contributions and your own contribution to the group work. Each
individual group member mark for group assignment will be weighted by the average of
the ratings including your self-assessment. The submission will be via Moodle. In case
of large discrepancies in ratings, further investigation will be conducted by the course
facilitator. Submit your team ratings and self-assessment by Monday, 8 August, 10:00
am Failure to submit team ratings and self-assessment will result in your individual mark
reduction for the group assignment by 10%.
Plagiarism All assignments will be checked for plagiarism. See notes on Plagiarism here.
2
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Time-line.
Week 6 Assignment released. Carefully read the assignment. Consider the method
you will use, the information you will need and where to get it. A team discussion about
all relevant aspects is expected. Due to social distancing, all discussion are expected to
happen online, via Moodle discussion forum, Skype or https://zoom.us. To help you
coordinating I suggest that the first member of the group as posted on Moodle hosts zoom
meeting in week 6 during your group tutorial time. Indeed, the group may decide on a
different meeting organiser/time, but make sure this does not fall through the cracks.
You may use https://doodle.com/ for scheduling. Break down the tasks and discuss
with your team mate about potential options. Each team member is expected to do some
part of each question. Draft a preliminary version of your team charter.
Week 7 Carry out a comprehensive study about relevant topics. Carefully consider
each sub-question. Examine thoroughly the relevant information. Consider your presen-
tation. It will be useful to draft a format template for everyone in the group to work on
it. Keep a record of your progress and each individual’s contribution faithfully. Submit
your team charter before the deadline.
Week 8 Solve the parts assigned to you using the knowledge from the course. Think
of how your part of the question will fit in the big picture.
Discuss with your team
mate(s) about the structure/organization of your project. Keep a record of your progress
and each individual’s contribution faithfully.
Week 9 Complete your assignment. Carefully address each sub-question, and organize
in a logical-coherent way. Paragraph your answer. Do not be reluctant to use full-stop.
Read each sentence again.
Make sure each sentence has a purpose, and it is clearly
understandable. Submit your assignment before the deadline.
Submission Format. The assignment should be typed and saved as pdf, and the pdf file
needs to be submitted before the deadline through the Moodle assignment submission.
You may insert some parts of hand-written text/calculations if is really necessary, but
make sure those are written really neatly and clearly readable. You may use https:
//smallpdf.com/word-to-pdf for conversion from word to pdf if necessary.
Cover Page Each submission should contain a cover page. The cover page should specify
the course “Economics of Finance”, “Group Assignment” and first and last names of
all the members of the group.
Body Text The submission should be divided into individual questions. The text should
be in either 1.5 or double-spaced typescript. The font size should be no less than 12
points (use 10 point for footnotes) in a legible font. Use A4 (297mm x 210mm) paper.
Include page numbers. The margins on each page should not be less than 30mm on the
left-hand side, 30mm on the right-hand side, 30mm at the top and 20mm at the bottom.
Diagrams, charts and tables and small code fragments should be presented within the
text. If you insert a code fragment, Courier New font gives a nice look to the code.
3
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Question 1. Duration and Banking (4 marks)
Consider a 5-year bond with annual coupon payments. The bond has a face value (prin-
cipal) of $100 and sells for $95. Its coupon rate is 3%. (The coupon rate is the ratio
between the coupon value and the face value). The face value is paid at the maturity
year in addition to the last coupon payment.
- Calculate the bond’s yield to maturity (YTM) and duration using its YTM. (1
mark) - Suppose the bond’s YTM changes in the same way as a 5-year T-bill interest rate.
Use the bond’s modified duration to evaluate the relative change in the 5-year bond’s
value if the interest rate on 5-year T-bills falls by one basis point, that is, by 0.0001.
(1 mark)
This part was extracted from the balance sheet of the First Bank of Australia:
Assets (Billion AUD)
Liabilities (Billion AUD)
Bond
80
Fixed-rate liabilities
60
where “Bond” here refers to the bond we specified above and the fixed-rate liabilities
(banks future payment obligations) have an average duration of 4 years and YTM of 3%.
Their YTM changes in the same way as a 5-year T-bill interest rate. - Bank’s equity is the difference between its assets and its liabilities. How does bank’s
equity change, if the T-bill interest rate increases by 10 basis point? (2 marks)
4
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Question 2. Option pricing (3 marks)
BHP Billiton, the leading Australian iron ore mining giant, is listed on New York Stock
Exchange. The iron ore prices have almost doubled from $67.87 on 3 August 2018 to
$123.16 on 3 July 2019. The following table shows BHP stock prices in $ and the an-
nualised historical volatility (Vol.) of BHP, VIX Index, the iron ore prices in $ at given
dates. For simplicity, we assume one price, i.e., no bid-ask spread.
Date
BHP stock price
Vol.(%)
VIX
Iron ore price
3 Jul 2019
58.93
19.5
12.6
123.16
3 Jun 2019
52.38
18.9
18.9
93.97
3 May 2019
52.81
17.1
12.9
89.15
3 Apr 2019
56.30
19.3
13.7
87.60
4 Mar 2019
52.79
16.4
14.6
78.98
4 Feb 2019
51.12
35.3
15.7
77.85
3 Jan 2019
46.39
33.9
16.4
74.30
3 Dec 2018
46.50
36.3
20.0
67.82
5 Nov 2018
48.40
32.4
14.2
74.17
4 Oct 2018
50.01
23.2
13.2
70.79
4 Sep 2018
47.24
27.6
11.6
68.28
3 Aug 2018
50.38
31.2
16.1
67.87
A European call option on BHP stock that expired on 3 Jan 2020 and had a strike
price of $65 was traded at $1.46 on 3 July 2019. A European put option on BHP stock
that expired on 3 Jan 2020 and had a strike price of $65 was traded at $8.55 on 3 July - The annual risk-free rate of interest was 2.15%. Using what you learnt from the
course, answer the following questions. Use discrete compounding if you need to compute
semi-annual interest rate. - Show that there was an arbitrage opportunity with these options. (1 mark)
- Construct an arbitrage strategy. (2 marks)
5
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Question 3. Real option (4 marks)
Option pricing methodology is often used in complex real project valuations which allow
for business investment opportunities throughout the life-time of the project. Using a
simple net present value (NPV) analysis for these projects may lead an incorrect valuation
because NPV does not account for flexibility of investment options.
Here is a specific example inspired by the article Sick and Gamba (2010). Suppose you
are a consultant hired by a local government. The government needs to raise some cash
now and hired you to determine the proper value of a three-year development concession
for a specific gold-mine which has 1 million ounces of gold reserves. It is known from past
practices that the gold can all be immediately produced in the year when the investment
is made for a combined capital and operating cost of $290 million (this amount does
not change within the three years). It is costly to store gold and it needs to be sold
immediately after it is produced.
Abstract from any additional financial instruments
which can be used for hedging as if they are fairly priced they will not improve our real
option. A company who purchases the concession will have the right to develop the mine
for the period of concession and will bear no additional tax obligations. An initial gold
price is $300 per ounce. From the analysis of historical data you know that gold price
will rise by 20% over a year with a probability of 0.65 and it will fall by 20% with a
probability of 0.35. The riskless discount rate is 6% and the company has can develop
now, or defer for either one or two years, after which point the opportunity to invest is
lost (concession expires). The government asked you to produce valuation of this project
from the perspective of the company (not including the concession fee since its value is
not decided yet). You were asked to assume that the company is risk-neutral.
6
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
You produce the figure above to explain your reasoning. It is analogous to American
option pricing. If immediately developed, the NPV of the project is $10 million, but
because the concession is valid for three periods (including period 0), the government
should charge a higher fee. - What is the maximum fee the government should charge for the concession? (1
mark) - Your contact person in the government, who recently studied Economic of Finance,
wants you to be more explicit about your calculations. In particular you are asked
to produce atomic prices for all future time-states g, b, gg, gb, bg, bb and calculate
the maximum value of the project using these atomic prices and future payments.
There are several ways to do this. You are free to use any method (incl. making
use of risk-neutrality). (2 marks for ECON3107, 1 mark for ECON5106) - Discuss how the atomic prices and the project valuation would change (qualitatively,
not the exact numbers), if the company was actually risk-averse rather than risk-
neutral. (1 mark) - ECON5106 only: read the article and explain how the real options create value.
(1 mark)
Reference
Sick, Gordon, and Andrea Gamba. “Some Important Issues Involving Real Options: An
Overview.” Multinational Finance Journal 14, no. 1/2 (2010): 73-123.
7
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Question 4. Arrow-Debreu Economy (7 marks)
Consider a world in which there are only two dates: 0 and 1. At date 1 there are three
possible states of nature: a good weather state (G), a fair weather state (F), and a bad
weather state (B). Denote S1 as the set of these states, i.e., s1 ∈ S1 = {G, F, B}. The
state at date zero is known. Denote probabilities of the three states as π = (0.4, 0.3, 0.3).
There is one non-storable consumption good, apple. There are three consumers in
this economy. Their preferences over apples are exactly the same and are given by the
following expected utility function
ck
0 + β
�
s1∈S1
πs1u
�
ck
s1
�
,
where subscript k = 1, 2, 3 denotes each consumer. In period 0, the three consumers have
a linear utility and, in period 1, the three consumers have the same instantaneous utility
function:
u © = c1−γ
1 − γ ,
where γ = 0.2 (the coefficient of relative risk aversion). The consumers’ time discount
factor, β, is 0.98.
The consumers differ in their endowments, which are given in the table below:
Endowments
t = 0
t = 1
s0
G
F
B
Consumer 1
0.4
3.2
1.8
0.9
Consumer 2
1.2
1.6
1.2
0.4
Consumer 3
2.0
1.2
0.6
0.2
Assume that atomic (Arrow-Debreu) securities are traded in this economy. One unit
of ’G security’ sells at time 0 at a price qG and pays one unit of consumption at time 1 if
state ’G’ occurs and nothing otherwise. One unit of ’F security’ sells at time 0 at a price
qF and pays one unit of consumption at time 1 if state ’F’ occurs and nothing otherwise.
One unit of ’B security’ sells at time 0 at a price qB and pays one unit of consumption in
state ’B’ only. - Write down the consumer’s budget constraint for all times and states, and define a
Market Equilibrium in this economy. Is there any trade of atomic (Arrow-Debreu)
securities possible in this economy? (1 mark) - Write down the Lagrangian for the consumer’s optimisation problem, find the first
order necessary conditions, and characterise the equilibrium (i.e., compute the op-
timal allocations and prices defined in the equilibrium). (2 marks) - At the equilibrium, calculate the forward price and risk premium for each atomic
security. What do your results suggest about the consumers’ preference? (1 mark)
8
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Suppose that instead of atomic (Arrow-Debreu) securities there are three linearly
independent securities, a riskless bond, a stock, and a one-period put option on this stock
available for trade in this economy. The riskless bond pays 1 apple in every state, the
stock pays 2, 1 and 0 apples in G, F and B, respectively. The put option has a strike
price of 1. - Write down the budget constraint for each consumer using the newly available
securities. (1 mark) - Write down the Lagrangian for the consumer’s optimisation problem, find the first
order necessary conditions, and characterise the equilibrium (i.e., compute equilib-
rium allocations and prices of the newly available securities). (1 mark) - Now, price the newly available securities using the atomic prices from part 2. Com-
ment on your results in light of the arbitrage-free markets. (1 mark)
9
c⃝Copyright University of New South Wales 2023. All rights reserved. This copyright notice must not
be removed from this material.
Question 5. Investment (2 marks)
Suppose the risk-free rate of return is 0.03. Market portfolio expected return is 0.10 and
its risk measured by standard deviation is 0.05.
There are two investors in the economy. Their expected utility functions are given by:
Eu = e − s2/ti, for i = 1, 2,
where risk tolerance t1 = 1 and t2 = 0.5. - Derive the Sharpe ratio of the market portfolio. Is there a stock in the market that
can beat this Sharpe ratio? (1 marks) - Derive the two individual investors’ portfolios. What are the expected return and
risk of each individual investor’s choice? Comment on your results. (1 mark