（简单）设计哈希集合 Java

news2024/9/23 13:12:19

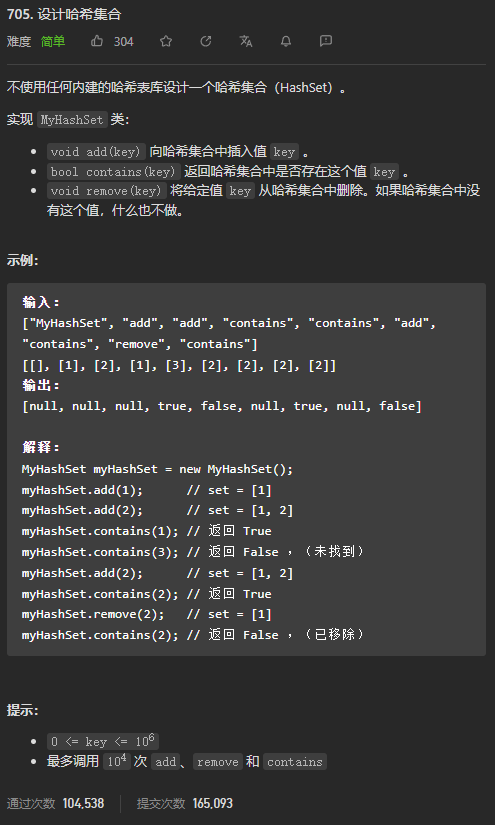
在这里插入图片描述

为了实现哈希集合这一数据结构，有以下几个关键问题需要解决：

哈希函数：能够将集合中任意可能的元素映射到一个固定范围的整数值，并将该元素存储到整数值对应的地址上
冲突处理：由于不同元素可能映射到相同的整数值，因此需要在整数值出现冲突时，需要进行冲突处理。总的来说，有以下几种策略解决冲突：
- 链地址法：为每一个哈希值维护一个链表，并将具有相同哈希值的元素都放入这一链表中
- 开放地址法：当发现哈希值h处产生冲突时，根据某种策略，从h出发找到下一个不冲突的位置。例如，一种最简单的策略是，不断地检查h+1，h+2，h+3，…这些整数对应的位置
- 再哈希法：当发现哈希冲突后，使用另一个哈希函数产生一个新的地址

方法一：简单数组法

依据提示创建了长度为10^6+1的数组set，如果向set中添加了某个数字x，则将set[x]置为1

class MyHashSet {

    private int[] set = new int[1000001];

    public MyHashSet() {

    }

    public void add(int key) {
        set[key] = 1;
    }

    public void remove(int key) {
        set[key] = 0;
    }

    public boolean contains(int key) {
        return set[key] != 0;
    }

}

在这里插入图片描述

方法二：链地址法

除了上面这种简单数组方法，也可以利用链表来构建set

设计哈希表大小为base，则可以设计一个简单的哈希函数：hash(x) = x mod base。

开辟一个大小为base的数组，数组的每个位置是一个链表。当计算出哈希值之后，就插入到对应位置的链表中。

由于该方法使用整数除法作为哈希函数，为了尽可能避免冲突，应当将base取为一个质数。

import java.util.Iterator;
import java.util.LinkedList;

class MyHashSet {

    private static final int BASE = 769;
    private LinkedList<Integer>[] data;

    public MyHashSet() {
        data = new LinkedList[BASE];
        for (int i = 0; i < BASE; i++) {
            data[i] = new LinkedList<>();
        }
    }

    public void add(int key) {
        int h = hash(key);
        Iterator<Integer> it = data[h].iterator();
        while (it.hasNext()) {
            Integer element = it.next();
            if (element == key) {
                return;
            }
        }
        data[h].addLast(key);
    }

    public void remove(int key) {
        int h = hash(key);
        Iterator<Integer> it = data[h].iterator();
        while (it.hasNext()) {
            Integer element = it.next();
            if (element == key) {
                data[h].remove(element);
                return;
            }
        }
    }

    public boolean contains(int key) {
        int h = hash(key);
        Iterator<Integer> it = data[h].iterator();
        while (it.hasNext()) {
            Integer element = it.next();
            if (element == key) {
                return true;
            }
        }
        return false;
    }

    private static int hash(int key) {
        return key % BASE;
    }
}