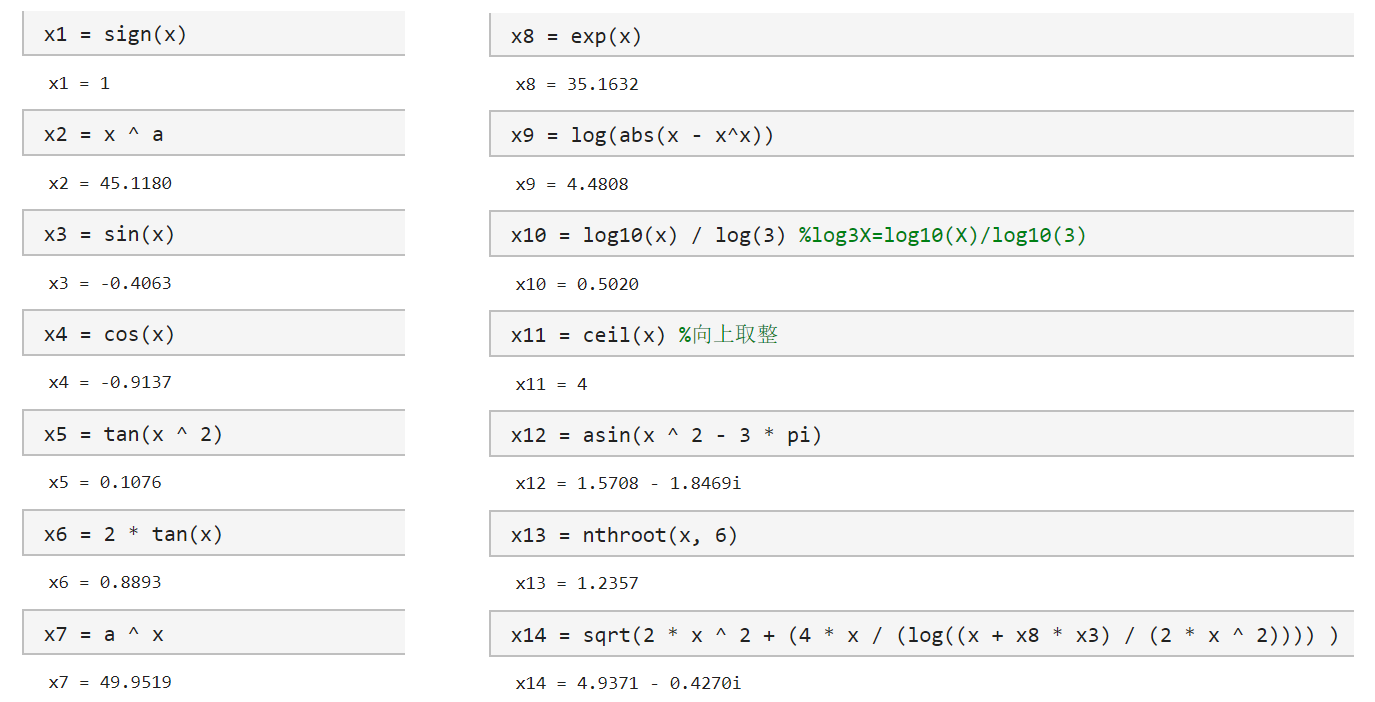
- 回忆你所学过的数学函数并给出x=3.56 时以下函数的值
s i g n ( x ) , x a ( a = 3 ) , sin ( x ) , cos ( x ) , tan ( x 2 ) , 2 tan ( x ) \begin{aligned}sign\left( x\right) ,x^{a}\left( a=3\right) ,\sin \left( x\right) ,\cos \left( x\right) ,\tan \left( x^{2}\right) ,2\tan \left( x\right) \end{aligned} sign(x),xa(a=3),sin(x),cos(x),tan(x2),2tan(x)
a x ( a = 3 ) , e x , ln ( ∣ x − x x ∣ ) , log 3 x , [ x ] , arcsin ( x 2 − 3 π ) , x 6 , 2 x 2 + 4 x ln x + e x sin x 2 x 2 \begin{aligned}a^{x}\left( a=3\right) ,e^{x},\ln \left( \left| x-x^{x}\right| \right) ,\log _{3}x,\left[ x\right] ,\\ \arcsin \left( x^{2}-3\pi \right) ,\sqrt[6] {x},\sqrt{2x^{2}+\dfrac{4x}{\ln \dfrac{x+e^{x}\sin x}{2x^{2}}}}\end{aligned} ax(a=3),ex,ln(∣x−xx∣),log3x,[x],arcsin(x2−3π),6x,2x2+ln2x2x+exsinx4x
%第一题
x = 3.56;
a = 3;
x1 = sign(x)
x2 = x ^ a
x3 = sin(x)
x4 = cos(x)
x5 = tan(x ^ 2)
x6 = 2 * tan(x)
x7 = a ^ x
x8 = exp(x)
x9 = log(abs(x - x^x))
x10 = log10(x) / log(3) %log3X=log10(X)/log10(3)
x11 = ceil(x) %向上取整
x12 = asin(x ^ 2 - 3 * pi)
x13 = nthroot(x, 6)
x14 = sqrt(2 * x ^ 2 + (4 * x / (log((x + x8 * x3) / (2 * x ^ 2)))) )
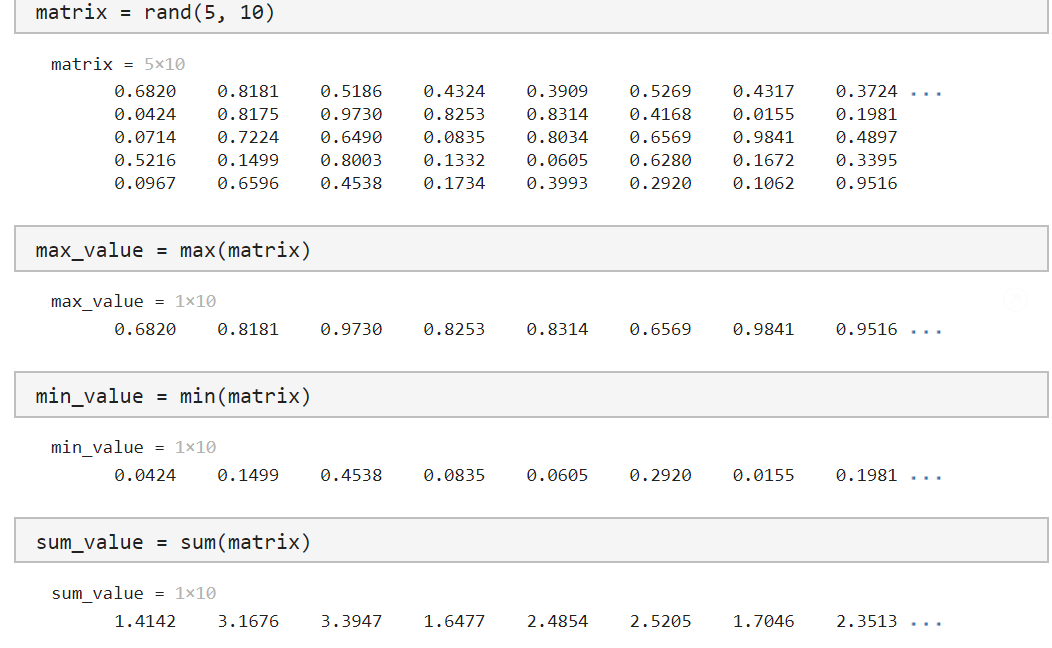
- 利用帮助了解向量函数max,min, sum,mean,sort,length,矩阵函数rand,size的功能和用法。操作步骤:先用函数rand生成一个5X10的矩阵再使用上面提到的函数,看看产生什么样的输出。并用自己的话说明上述函数的功能和用法。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-s1xL7CN2-1689390045172)(https://raw.githubusercontent.com/lucasZyh/Personal-picture-bed/master/img/202307151057489.png)]
向量函数:
max:返回向量中的最大值。 用法:max(vector)
min:返回向量中的最小值。 用法:min(vector)
sum:返回向量中所有元素的总和。 用法:sum(vector)
mean:返回向量中所有元素的平均值。 用法:mean(vector)
sort:对向量进行排序,按升序排列。 用法:sort(vector)
length:返回向量中的元素个数。 用法:length(vector)
矩阵函数:
rand:生成指定大小的随机矩阵,元素值在0和1之间。 用法:rand(rows, columns)
size:返回矩阵的大小(行数和列数)。 用法:size(matrix)
%第二题
%2.利用帮助了解向量函数max,min, sum,mean,sort,length,
% 矩阵函数rand,size的功能和用法。
% 操作步骤:先用函数rand生成一个5X10的矩阵再使用上面提到的函数,看看产生什么样的输出。
% 并用自己的话说明上述函数的功能和用法。
matrix = rand(5, 10)
max_value = max(matrix)
min_value = min(matrix)
sum_value = sum(matrix)
mean_value = mean(matrix)
sorted_matrix = sort(matrix)
matrix_length = length(matrix)
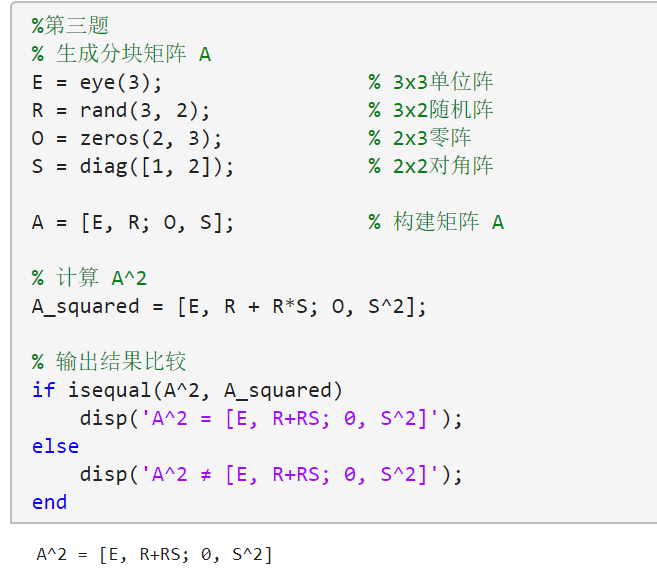
3.设有分块矩阵 A = [ E 3 × 3 R 3 × 2 O 2 × 3 S 2 × 2 ] A=\begin{bmatrix} E_{3\times 3} & R_{3\times 2} \\ O_{2\times 3} & S_{2\times 2} \end{bmatrix} A=[E3×3O2×3R3×2S2×2]其中E,R,O,S分别为单位阵、随机阵、零阵和对角阵,试编写一个命令M文件,技术验证 A 2 = [ E R + R S 0 S 2 ] A^{2}=\begin{bmatrix} E & R+RS \\ 0 & S^{2} \end{bmatrix} A2=[E0R+RSS2]。提示:先产生一个矩阵A,计算出A;另一方面,计算矩阵 [ E R + R S 0 S 2 ] \begin{bmatrix} E & R+RS \\ 0 & S^{2} \end{bmatrix} [E0R+RSS2],比较结果是否一致。
%第三题
% 生成分块矩阵 A
E = eye(3); % 3x3单位阵
R = rand(3, 2); % 3x2随机阵
O = zeros(2, 3); % 2x3零阵
S = diag([1, 2]); % 2x2对角阵
A = [E, R; O, S]; % 构建矩阵 A
% 计算 A^2
A_squared = [E, R + R*S; O, S^2];
% 输出结果比较
if isequal(A^2, A_squared)
disp('A^2 = [E, R+RS; 0, S^2]');
else
disp('A^2 ≠ [E, R+RS; 0, S^2]');
end
- 在同一个坐标下作出$y_{1}=x,y_{2}=x-\dfrac{x{3}}{3!},y_{3}=x-\dfrac{x{3}}{3!}+\dfrac{x^{5}}{5!},y_{4}=\sin \left( x\right) $,这四条曲线的图形,说明 Taylor 公式说明了什么问题。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hUxs6xh0-1689390045173)(https://raw.githubusercontent.com/lucasZyh/Personal-picture-bed/master/img/202307151057490.png)]
Taylor 公式是一种用无穷级数展开来逼近函数的方法。它可以将一个函数在某个点附近的局部行为用多项式来表示。y1 = x 就是函数 f(x) = x 在 x = 0 处的一阶泰勒展开式,y2 和 y3 分别是 f(x) = sin(x) 在 x = 0 处的三阶和五阶泰勒展开式。通过绘制这些曲线,我们可以观察到泰勒展开式在给定点附近的逼近效果。Taylor 公式说明了在某个点附近,一个光滑函数可以用一个多项式逼近。通过增加多项式的阶数,我们可以获得更高精度的逼近结果。
%第四题
x = linspace(-2*pi, 2*pi, 100); % 生成 x 的取值范围
y1 = x;
y2 = x - x.^3/factorial(3);
y3 = x - x.^3/factorial(3) + x.^5/factorial(5);
y4 = sin(x);
% 绘制曲线
figure;
hold on;
plot(x, y1, 'b', 'LineWidth', 2);
plot(x, y2, 'r', 'LineWidth', 2);
plot(x, y3, 'g', 'LineWidth', 2);
plot(x, y4, 'm', 'LineWidth', 2);
xlabel('x');
ylabel('y');
legend('y_1 = x', 'y_2 = x - x^3/3!', 'y_3 = x - x^3/3! + x^5/5!', 'y_4 = sin(x)');
title('Taylor公式的示例');
hold off;
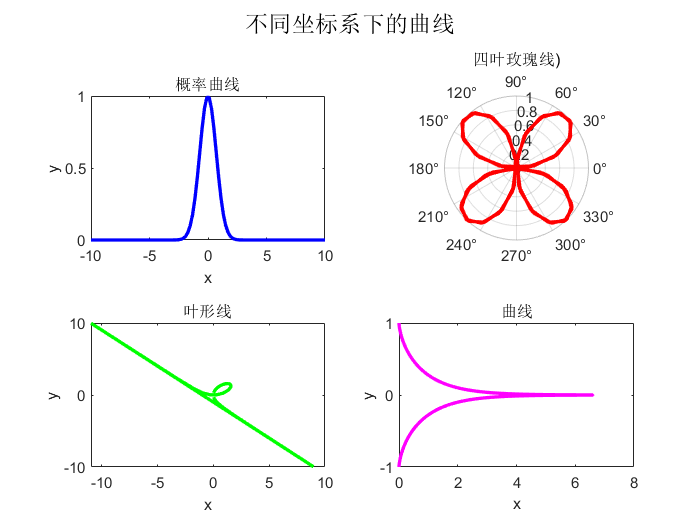
- 用 subplot 分别在不同的坐标系下作出四条曲线
(1)概率曲线 y = e − x 2 y=e^{-x^{2}} y=e−x2
(2)四叶玫瑰线$\rho =\sin 2\theta $
(3)叶形线 { x = 3 t 1 + t 3 y = 3 t 2 1 + t 3 \begin{cases}x=\dfrac{3t}{1+t^{3}}\\ y=\dfrac{3t^{2}}{1+t^{3}}\end{cases} ⎩ ⎨ ⎧x=1+t33ty=1+t33t2
(4) x = ln 1 + 1 − y 2 y − 1 − y 2 x=\ln \dfrac{1+\sqrt{1-y^{2}}}{y}-\sqrt{1-y^{2}} x=lny1+1−y2−1−y2
%第五题 用 subplot 分别在不同的坐标系下作出四条曲线
t = linspace(-10, 10, 100); % 生成 t 的取值范围
% 概率曲线 y = e^(-x^2)
x1 = t;
y1 = exp(-x1.^2);
% 四叶玫瑰线 rho = sin(2*theta)
theta = t;
rho = sin(2*theta);
% 叶形线
x3 = 3*t./(1 + t.^3);
y3 = 3*t.^2./(1 + t.^3);
% x = ln((1 + sqrt(1-y^2))/y) - sqrt(1-y^2)
y4 = linspace(-1, 1, 1000);
x4 = log((1 + sqrt(1 - y4.^2))./y4) - sqrt(1 - y4.^2);
% 绘制四个子图
figure;
% 子图1:概率曲线
subplot(2, 2, 1);
plot(x1, y1, 'b', 'LineWidth', 2);
xlabel('x');
ylabel('y');
title('概率曲线');
% 子图2:四叶玫瑰线
subplot(2, 2, 2);
polarplot(theta, rho, 'r', 'LineWidth', 2);
title('四叶玫瑰线)');
% 子图3:叶形线
subplot(2, 2, 3);
plot(x3, y3, 'g', 'LineWidth', 2);
xlabel('x');
ylabel('y');
title('叶形线');
% 子图4:曲线 x = ln((1 + sqrt(1-y^2))/y) - sqrt(1-y^2)
subplot(2, 2, 4);
plot(x4, y4, 'm', 'LineWidth', 2);
xlabel('x');
ylabel('y');
title('曲线');
% 调整子图之间的间距
sgtitle('不同坐标系下的曲线');
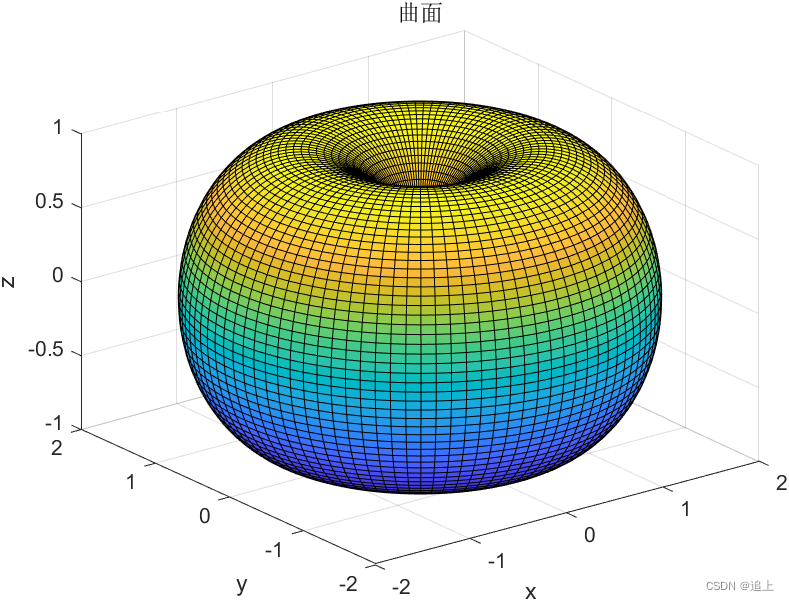
- 做出曲面 { x = ( 1 + cos u ) cos v , y = ( 1 + cos u ) sin v , u ∈ ( 0 , 2 π ) Z = sin u , v ∈ ( 0 , 2 π ) \begin{cases}x=\left( 1+\cos u\right) \cos v,\\ y=\left( 1+\cos u\right) \sin v,u\in \left( 0,2\pi \right) \\ Z=\sin u,v\in \left( 0,2\pi \right) \end{cases} ⎩ ⎨ ⎧x=(1+cosu)cosv,y=(1+cosu)sinv,u∈(0,2π)Z=sinu,v∈(0,2π)
%第六题
u = linspace(0, 2*pi, 100); % 生成 u 的取值范围
v = linspace(0, 2*pi, 100); % 生成 v 的取值范围
[u, v] = meshgrid(u, v); % 生成网格点
% 参数方程
x = (1 + cos(u)) .* cos(v);
y = (1 + cos(u)) .* sin(v);
z = sin(u);
% 绘制曲面
figure;
surf(x, y, z);
xlabel('x');
ylabel('y');
zlabel('z');
title('曲面');
- 利用 for 循环求 1! +2! +3!+ …+5!的值。
153
%第七题
n = 5; % 求和的最大阶乘值
sum = 0; % 初始化求和结果
for k = 1:n
sum = sum + factorial(k); % 累加到求和结果
end
disp(sum); % 输出结果
- 已知一维数组 A=[2,4,5,8,10],B=[4,6,9,3,4],用 for 循环语句实现 ∑ i = 1 n A i B n − i + 1 \sum ^{n}_{i=1}A_{i}B_{n-i+1} ∑i=1nAiBn−i+1求和函数可用 sum()。
153
%第八题
A = [2, 4, 5, 8, 10];
B = [4, 6, 9, 3, 4];
n = length(A);
result = 0;
for i = 1:n
result = result + A(i) * B(n - i + 1);
end
disp(result);
B=[4,6,9,3,4],用 for 循环语句实现 ∑ i = 1 n A i B n − i + 1 \sum ^{n}_{i=1}A_{i}B_{n-i+1} ∑i=1nAiBn−i+1求和函数可用 sum()。
153
%第八题
A = [2, 4, 5, 8, 10];
B = [4, 6, 9, 3, 4];
n = length(A);
result = 0;
for i = 1:n
result = result + A(i) * B(n - i + 1);
end
disp(result);

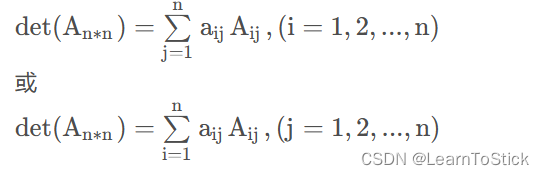







![考核:QTableWidget开发[折叠/展开单元格QTableWidgetItem]](https://img-blog.csdnimg.cn/9ce1011df8cd48ec84ea81c5c824c0b5.png)