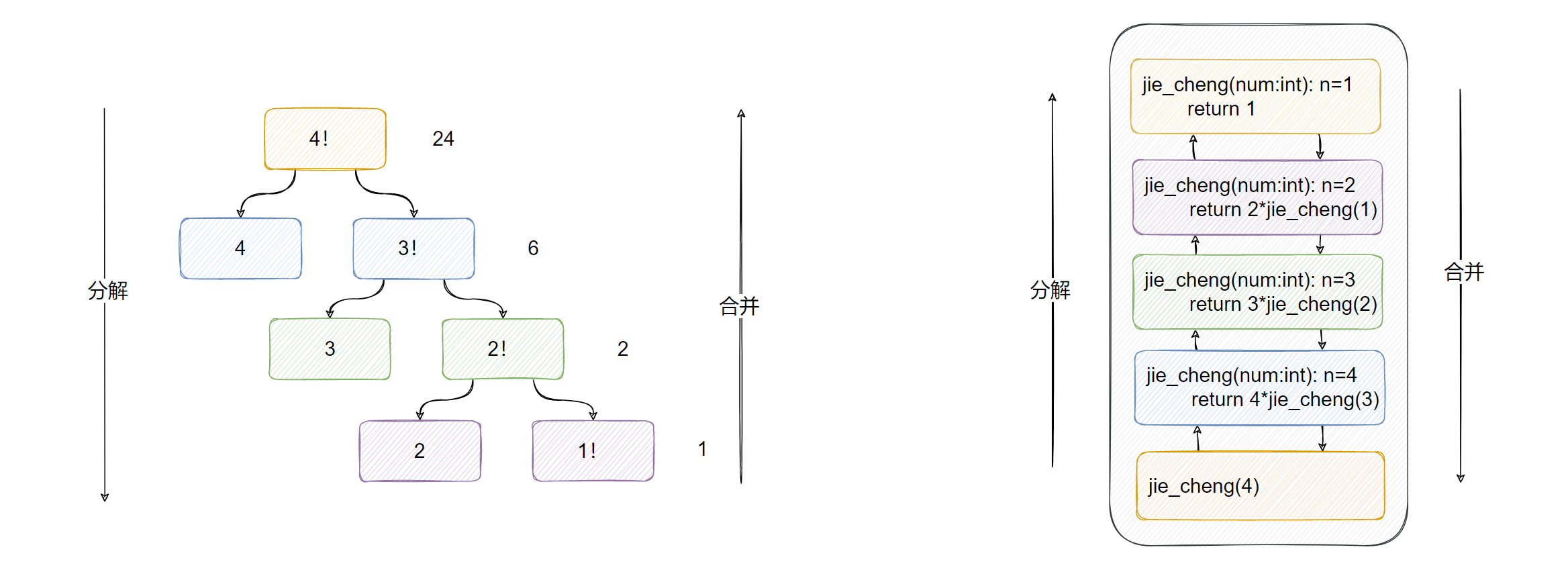
举例：

1.暴力计算

2.通过代数余子式计算

相关理论：

  这个C就是上图的Aij哈，我拷的别人的图。

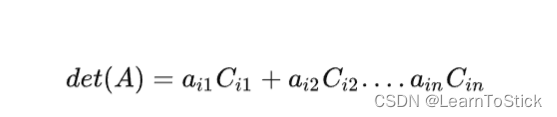
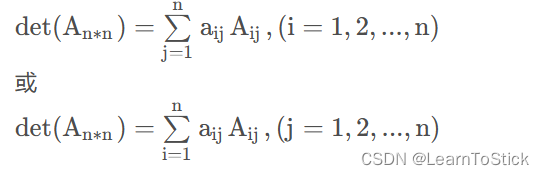
可以得出，行列式的值可以按照某行展开，展开后余子式即为一个新的行列式，就是原行列式删除某一行一列之后得到的行列式，用此思想可以得出代码如下：

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <numeric>
#include <set>
#include <queue>

using namespace std;

// 行列式
int cal(int **det, int n) {
  if (n == 1)
    return det[0][0];
  int res = 0;
  // 存储余子式
  int **tmp = new int *[n-1];
  for (int i = 0; i < n - 1; i++)
    tmp[i] = new int[n - 1];
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n - 1; j++) {
      for (int k = 0; k < n - 1; k++) {
        // 计算余子式 M(i,j)
        if (k < i)
         tmp[j][k] = det[j + 1][k];
        else
         tmp[j][k] = det[j + 1][k + 1];
      }
    }
    // 按行展开递归计算下一个余子式 （即行列式）
    res += det[0][i] * pow(-1, i) * cal(tmp, n - 1);
  }
  return res;
}

int main(){
  int n;
  cout << "input step: ";
  cin >> n;
  int **det = new int*[n];
  for (int i = 0; i < n; i++)
    det[i] = new int[n];
  cout << "input matrix: " << endl;
  for (int i = 0; i < n; i++)
    for (int j = 0; j < n; j++)
      cin >> det[i][j] ;
  cout << "result is: " << cal(det, n) << endl;
}

此方法缺点：计算的阶数有限，可用其他思路，初等变换， 逆序数全排列自行搜索哦。