目录
- 一、深度优先搜索与回溯
- 1、四阶数独
- 2、排列类问题
- 3、红与黑(dfs或bfs和Flood fill)
之前学习了暴力枚举策略,将所有可能的情况都枚举一遍以获得最优解,但是枚举全部元素的效率如同愚公移山,无法应付数据范围稍大的情形。
本节在暴力枚举的基础上介绍搜索算法,包括 深度优先搜索和广度优先搜索, 从起点开始,逐渐扩大寻找范围,直到找到需要的答案为止
严格来说,搜索算法也算是种暴力枚举策略,但是其算法特性决定了效率比直接的枚举所有答案要高,因为搜索可以跳过一些无效状态,降低问题规模。在算法竞赛中,如果选手无法找到一种高效求解的方法(如贪心递推、动态规划公式推导等,使用搜索也可以解决一些规模较小的情况;而有的任务就是必须使用搜索来完成,因此这是相当重要的策略。
一、深度优先搜索与回溯
DFS模板(回溯):
dfs和回溯的关系(没用,可以不看)
主要用于解决:排列问题,组合问题,切割问题,棋盘问题等
void dfs(int k){
//k代表递归层数,也就是填写到第几个空了,或者搜索到第几个空
if(k>=n){//空已经填完了
判断最优解/记录答案/输出符合要求的排列
return;
}
for(int i = 0; i < ;i++){
//枚举提供给这个空填写的选项;迷宫类问题是枚举四个方位
if(jugde(i)){ //判断这个选项是合法的,如:判断边界;特殊条件判断
记录这个空填的数以及对应的状态值修改
dfs(k+1)// 继续判断下一层
取消对当前这个空的处理 恢复现场
}
}
}
1、四阶数独
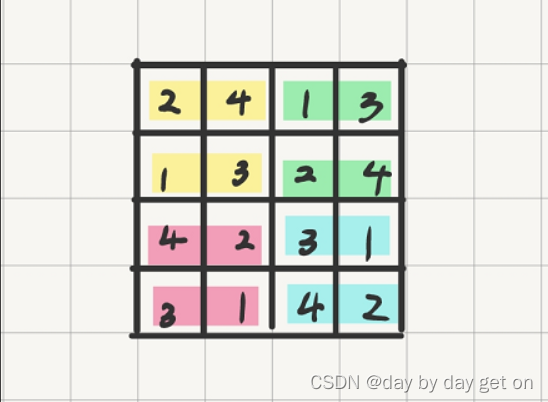
数独是一种著名的益智游戏,这里讨论的是一种简化后的数独-四阶数独,给出一个4*4的方格,每个格子只能填写1-4的整数,要求每行每列和四等分更小的正方形部分刚好都由1-4组成,每行每列,每小块不能有重复的数字出现。
请问:一共有多少种合法的填写方案?
具体解析,见洛谷【深基.14 搜索】p188
这个博主讲得也还可以:链接
解题代码:
#include<bits/stdc++.h>
using namespace std;
int b1[5][5],b2[5][5],b3[5][5]; 分别标记每行、每列、每个小块出现的数字
int cnt=0;
int g[20]; //记录棋盘
void dfs(int x){
if(x>16){ //如果取够数
cnt++;
/*打印所有方案
for(int i = 1; i <= 16;i++){
cout<<g[i]<<" ";
if(i%4==0) cout<<endl;
}
cout<<endl;
*/
}
int row = (x-1)/4 + 1; //找到这个空在第几行
int col = (x-1)%4 + 1; //得到这个空在第几列
int exd;//一共就四个块 可以特判 也可以直接用规律
exd = (row-1)/2*2 + (col-1)/2 +1;// 根据行列值,四个小块可以表示为0++0+1 0+1+1 2+0+1 2+1+1四种情况
for(int i = 1; i <= 4; i++){
//cout<<k<<" "<<i<<endl;
if(b1[row][i]==0&&b2[col][i]==0&&b3[exd][i]==0){ //判断是否符合条件
g[x] = i; //保存结果
b1[row][i]=1; b2[col][i]=1; b3[exd][i]=1;//保存状态(占位)
//cout<<g[k]<<endl;
dfs(x+1);//下一层递归
b1[row][i]=0; b2[col][i]=0; b3[exd][i]=0; //恢复状态 (取消占位)
}
}
}
//memset(b1,0,sizeof(b1));
int main(){
dfs(1);
cout<<cnt;
return 0;
}
2、排列类问题
遇到了需要枚举排序的时候,搜索回溯会很好用。不需要生成所有的序列全排列,而是一一个一个地填空,保证填空的时候序列是合法的,这样就可以不用枚举很多无效序列,节约程序运行时间。
枚举的三大类型:博客链接
1、递归实现指数型枚举:
主要题干:从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。 同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。对于没有选任何数的方案,输出空行。本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。状态空间规模:2n
思路: 递归搜索树,对每一个数字,有选和不选它,两种状态,放入到答案数组里面。递归选和不选两个子解空间就行了。
#include<bits/stdc++.h>
using namespace std;
vector<int> ans;
int n;
void solve(int x){
if(x>n){
for(int i = 0; i < ans.size(); i++){
printf("%d ",ans[i]);
}cout<<'\n';
return;
}
solve(x+1); //这个位置的数,没被选择; 进入下一个空
ans.push_back(x);
solve(x+1); //这个位置的数,被选择; 进入下一层
ans.pop_back(); //回到上一层时,这个数是没有杯加入到答案数列里面的
}
int main(){
cin>>n;
solve(1);
return 0;
}
2、递归实现组合型枚举:
主要题干:从 1∼n 这 n 个整数中随机选出 m 个,输出所有可能的选择方案。 首先,同一行内的数升序排列,相邻两个数用一个空格隔开。其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如 1 3 5 7 排在 1 3 6 8 前面)。
状态空间规模:C(nm)
思路:在指数型枚举的基础上,进行剪枝,本题中, 如果已经选择了超过m个数,或者即使再选上剩余所有的数也不够m个,就可以提前返回了。 因为无解。
#include<bits/stdc++.h>
using namespace std;
vector<int> ans;
int n,m;
void solve(int x){
if(ans.size()>m||(ans.size()+n-x+1)<m) return;
if(x>n){
for(int i = 0; i < m; i++){
printf("%d ",ans[i]);
}cout<<'\n';
return;
}
//先进行“选”的分支,这样字典序小的才能在前面
ans.push_back(x);
solve(x+1); //这个位置的数,被选择; 进入下一层
ans.pop_back(); //回到上一层时,这个数是没有杯加入到答案数列里面的
solve(x+1); //这个位置的数,没被选择; 进入下一个空
}
int main(){
cin>>n>>m;
solve(1);
return 0;
}
3、递归实现排列型枚举(全排列)
把 1∼n 这 n 个整数排成一行后随机打乱顺序,输出所有可能的次序。
状态空间规模:n!
1、2 与3 的做法是有一些不一样的,全排列的做法是规规矩矩的dfs模板做法。
#include<bits/stdc++.h>
using namespace std;
int n;
int ans[550],stu[550];
void dfs(int x){
if(x>n){
for(int i = 1; i< n+1;i++){
printf("%d ",ans[i]);
}cout<<'\n';
}
for(int i = 1; i <= n; i++){
if(stu[i]==0){
stu[i]=1; ans[x]= i;
dfs(x+1);
stu[i] = 0; ans[x] = 0;
}
}
}
int main(){
cin>>n;
dfs(1);
return 0;
}
Dfs求解有重复元素的全排列
重点是可填写数据的遍历和符合条件判断。
https://blog.csdn.net/qq_52626583/article/details/123572390?spm=1001.2014.3001.5502
#include<stdio.h>
char s[550]; //读入字母元素
int num[27];
char p[550]; //输出字母元素
int n;
int sum = 0;
void dfs(int x){
if(x==n){ //填写长度为n的序列
sum++;
printf("%s\n",p);
}else{
for(int i = 1; i <=26;i++){ //可用于填写的所有字母
if(num[i]){ //判断这个字母还有才能用于填写
p[x] = i-1 + 'a' ;
num[i]--;
dfs(x+1);
num[i]++;
}
}
}
}
int main(){
scanf("%d",&n);scanf("%s",s);
for(int i = 0; i< n;i++){
num[s[i]-'a'+1] ++;
}
dfs(0);
printf("%d",sum);
return 0;
}
3、红与黑(dfs或bfs和Flood fill)
题目链接
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式:
输入包括多个数据集合。
每个数据集合的第一行是两个整数 W 和 H,分别表示 x 方向和 y 方向瓷砖的数量。
在接下来的 H 行中,每行包括 W 个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出格式:
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
数据范围:
1≤W,H≤20
输入样例:
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
输出样例:
45
解题思路:
AC代码: bfs!
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int N = 25;
char g[N][N];
int n,m;
int dx[5] = {-1,0,1,0},dy[5] = {0,1,0,-1};
struct node{
int x,y;
}tmp;
int bfs(int sx,int sy){
int res = 0;
queue<node> q;
q.push({sx,sy});
g[sx][sy] = '#';
while(q.size()){
tmp = q.front();
q.pop();
res++;
for(int i = 0; i <4;i++){
int x = tmp.x + dx[i],y = tmp.y + dy[i];
if(x<0||x>=n||y<0||y>=m||g[x][y]=='#') continue;
q.push({x,y});
g[x][y] = '#';
}
}
return res;
}
int main(){
int ans = 0;
while(cin>>m>>n,m||n){
for(int i = 0; i < n;i++) cin>>g[i];
for(int i = 0;i <n;i++){
for(int j = 0; j <m;j++){
if(g[i][j]=='@') ans = bfs(i,j);
}
}
cout<<ans<<endl;
}
return 0;
}
AC代码 dfs!
#include <cstring>
#include <iostream>
using namespace std;
const int N = 25;
int n, m;
char g[N][N];//存储地板
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//上右下左四个方向
int dfs(int x, int y)//深度优先遍历
{
int cnt = 1;
g[x][y] = '#';
for (int i = 0; i < 4; i ++ )//走四个方向
{
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= n || b < 0 || b >= m) continue;
if (g[a][b] != '.') continue;
cnt += dfs(a, b);//如果可以走向某一个方向,对该方向上的点递归
}
return cnt;
}
int main()
{
int ans;
while (cin >> m >> n, n || m){
for (int i = 0; i < n; i ++ ) cin >> g[i];//一次读入一行
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (g[i][j] == '@') ans = dfs(i,j);
cout << ans << endl;
}
return 0;
}
](https://img-blog.csdnimg.cn/9a639a1eac2f440bb6146b5d5c4a065b.png#pic_center)