1 题目

题目

3个A合成1个B

方案1：1/4 几率返还一个A，

方案2：1/10 几率多得1个B

哪一个更好呢？

2 结论

期望差不多的时候，应该要考虑方差小的，也就是概率差不多的感受更好

所以，这2个方案里方案1更好

3 算法

3.1 错误算法

下面这是错的！

这种简单思维，完全没有考虑到递归的影响，绿色还可以继续再来合成，需要折算

方案1

=1/4*（3+1）+3/4*3
=4/4+9/4
=13/4

方案2

=9/10*3+1/10*6
=27/10+6/10
=33/10

比较

E(X1)-E(X2)=11/4-33/10=（110-132）/40= -22/40= -11/20

3.2 算法1，用期望的方式解方式

这里

把A视为E(X), 把B视为1，每1个A只相当于1/3个B

解方程，算期望
其实，其实是用1个A，3个A，或者12个A都可以的，最后都可以约掉

方案1

把A视为E(X), 把B视为1，每1个A只相当于1/3个B

E(X1)=1/4*1/3（1+E(X)）+3/4*1/3
E(X1)=1/12*（1+E(X)）+3/12
11/12*E(X1)=4/12
E(X1)=4/11

方案2

E(X2)=9/10*1/3+1/10*2*(1/3)
E(X2)=3/10+2/30
E(X2)=11/30

比较

E(X1)-E(X2)=4/11-11/30= (120-121) /330 = -1/330

3.3 算法2，直接解方程

方案1

解方程，算二者关系

把A视为A, 把B视为B，每3个A可以合成一次B

3A=3/4*B+1/4*(B+A)
11/4*A=B
A=4/11*B

方案2

3A=9/10*B+1/10*2B
3A=11/10*B
A=11/30*B

比较

E(X1)-E(X2)=4/11-11/30= (120-121) /330 = -1/330

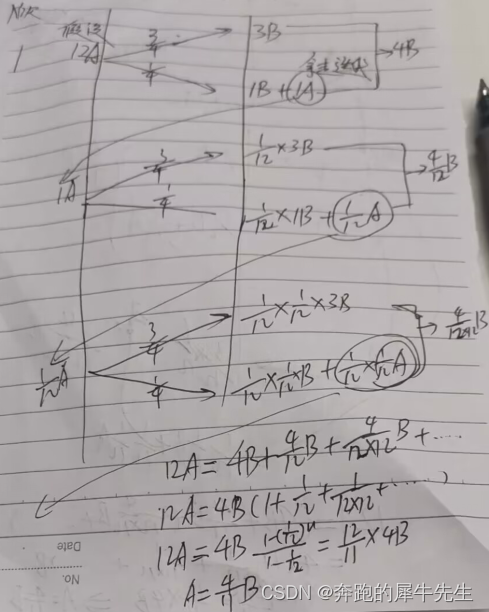
3.4 算法3，用递归--等比数列求和来算

用递归的方法算

考虑到递归的影响，绿色还可以继续再来合成，需要折算

考虑递归--用等比数列求和的方式算

方式1

需要根据现在的合成关系，去展开
然后去观察下，每次迭代之间的数值关系
确实是符合等比数量
找到公比，后来就好计算了

方式2

这个不用递归

因为没有涉及到合成后又生成A的问题

3A=9/10*B+1/10*2B
3A=11/10*B
A=11/30*B

比较

E(X1)-E(X2)=4/11-11/30= (120-121) /330 = -1/330