🚀write in front🚀
📝个人主页:认真写博客的夏目浅石.
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:鹏哥带我学c带我飞
💬总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🖊
✉️不如沉默去做,看结局怎么去说 ♐
文章目录
- 前言
- 1. 🌸什么是函数递归
- 2. 🏵️递归的两个必要条件
- 2.1 练习1:打印一个数的每一位
- 2.2 练习2:求字符串长度(strlen 模拟实现)
- 3. 💐递归与迭代
- 3.1练习3:求 n 的阶乘(不考虑溢出)
- 3.1.2 迭代(非递归)求n的阶乘
- 3.2 练习4:求第 n 个斐波那契数(不考虑溢出)
- 3.2.1 递归求第 n 个斐波那契数
- 3.2.2 迭代(非递归)求第n个斐波那契数
- 4.🌻补充练习
- 4.1 计算一个数的每位之和(递归实现)
- 4.2 写一个函数实现n的k次方(递归实现)
- 4.3 字符串逆序
- 4.3.1 非递归实现字符串逆序
- 4.3.2 递归实现字符串逆序
- 🌺结语
前言
上次函数剩下一个递归没讲,今天我想写一下函数递归这个内容
1. 🌸什么是函数递归
程序调用自身的编程技巧称为递归( recursion)。
递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接
调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小。
2. 🏵️递归的两个必要条件
(1) 存在限制条件,当满足这个限制条件的时候,递归便不再继续。
(2) 每次递归调用之后越来越接近这个限制条件
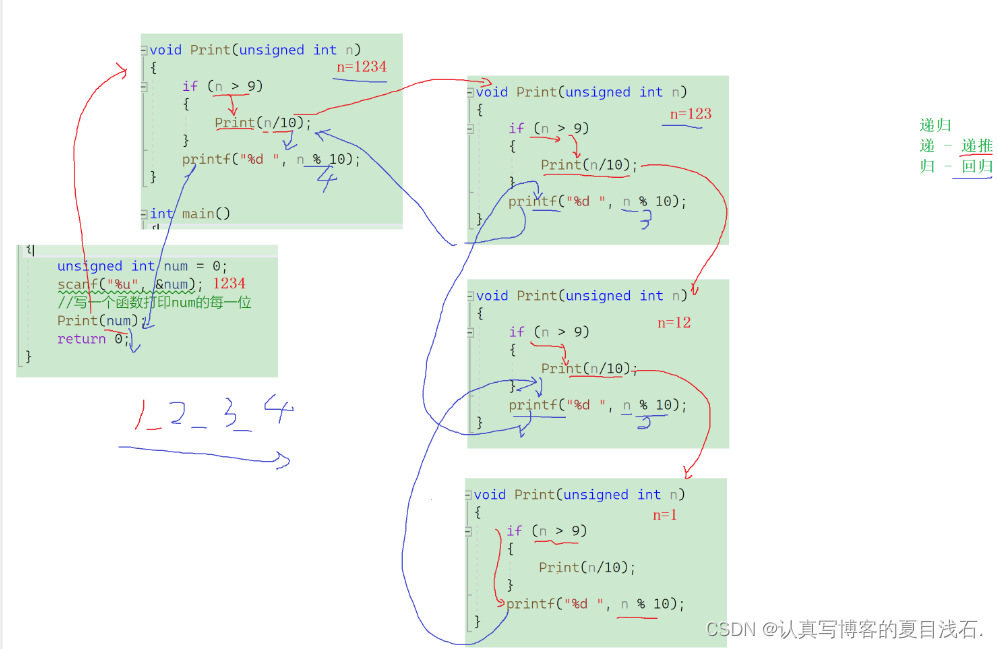
2.1 练习1:打印一个数的每一位
接受一个整型值(无符号),按照顺序打印它的每一位。
示例:
输入:1234,
输出: 1 2 3 4
思路:
- 递归就是把大事化小,函数自己调用自己。
- 按照顺序打印他的每一位,我们就用1234%10就会等于4,这样就打印出一个4了,那怎么打印其他的呢?123怎么来呢?1234/10=123,再继续123%10就等于3以此类推。
- 这里我们写一个 print 函数,让print函数自己调用自己实现递归。if 语句判断 n 是否是个位数,当 n 是个位数就直接打印n%10;当 n 不是个位数就先 n/10,再打印 n %10
#include <stdio.h>
void print(unsigned int n)
{
if (n > 9)
{
print(n / 10);
}
printf("%d ", n % 10);
}
int main()
{
unsigned int num = 0;
scanf("%u", &num);
print(num);//按照顺序打印num的每一位
return 0;
}
图解:

2.2 练习2:求字符串长度(strlen 模拟实现)
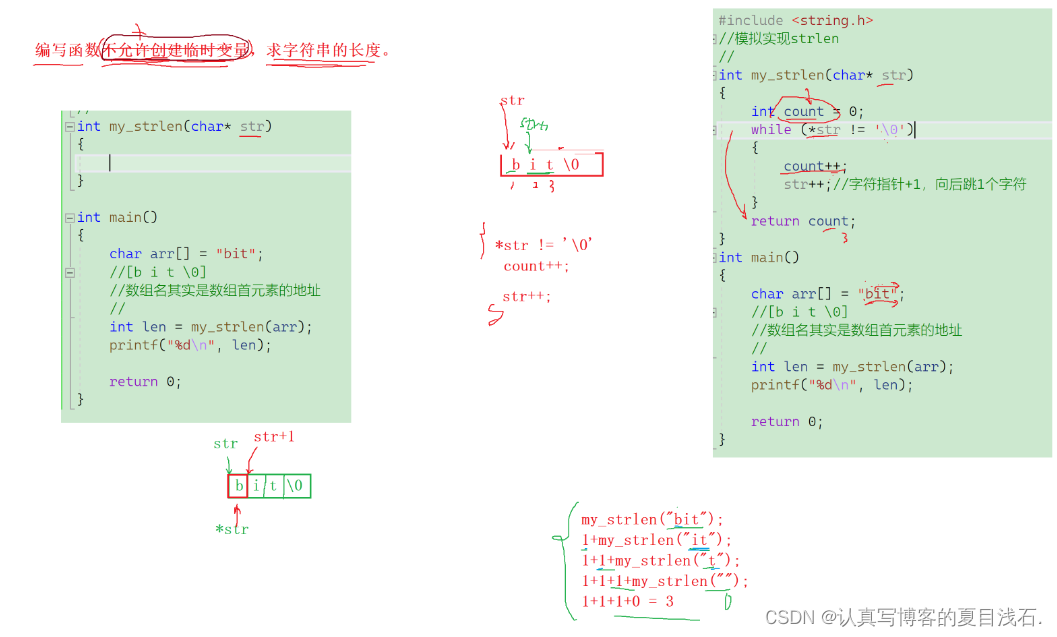
编写函数不允许创建临时变量,求字符串的长度。
示例:
输入:abc
输出:3
思路:
递归就是把大事化小,函数自己调用自己。
strlen 求字符串长度就是遇到 \0 才会停下。
我们要计算一个字符串的长度,字符串为 abc,我们可以把 my_strlen(arr) 转化成:
my_strlen(“abc”)
1+my_strlen(“bc”)
1+1+my_strlen(“c”)
1+1+1+my_strlen(" ") //空字符里面有 \0
#include <stdio.h>
#include <string.h>
int my_strlen(char* str)
{
if (*str != '\0')
return 1 + my_strlen(str + 1);
else
return 0;
}
int main()
{
char arr[] = "abc";
int len = my_strlen(arr);
printf("%d\n", len);
return 0;
}
图解:
3. 💐递归与迭代
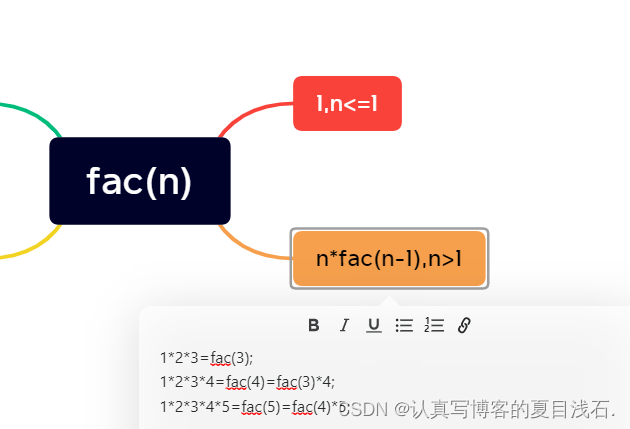
3.1练习3:求 n 的阶乘(不考虑溢出)
示例:
输入:5
输出:120
//递归求n的阶乘
#include <stdio.h>
int Fac(int n)
{
if (n <= 1)
return 1;
else
return n * Fac(n - 1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fac(n);
printf("%d\n", ret);
return 0;
}
3.1.2 迭代(非递归)求n的阶乘
//迭代(非递归)求n的阶乘
#include <stdio.h>
int Fac(int n)
{
int i = 0;
int ret = 1;
for (i = 1; i <= n; i++)
{
ret = ret * i;
}
return ret;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fac(n);
printf("%d\n", ret);
return 0;
}
总结:
一个问题既可以用递归的方式求解也可以用非递归的求解,非递归就是迭代,无论是递归的方式还是非递归的方式都很容易理解。迭代是指一件事情反复去做,但是迭代不一定是循环,循环是迭代的一种情况。
3.2 练习4:求第 n 个斐波那契数(不考虑溢出)
3.2.1 递归求第 n 个斐波那契数
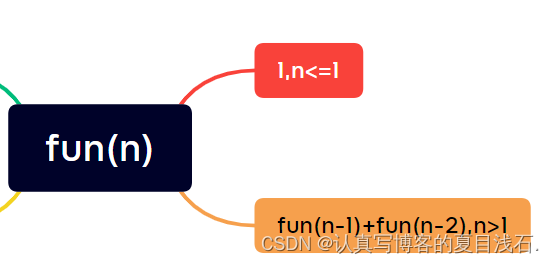

//递归实现
#include <stdio.h>
int Fib(int n)
{
if (n <= 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}
但是我们发现有问题:
在使用 fib 这个函数的时候如果我们要计算第40个斐波那契数字的时候特别耗费时间。为什么呢?我们发现 fib 函数在调用的过程中很多计算其实在一直重复。我们将代码修改一下:
#include <stdio.h>
int count = 0;//全局变量
int Fib(int n)
{
if (n == 3)
count++;
if (n <= 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
printf("count=%d\n",count);
return 0;
}
看输出结果我们会发现 count 是一个很大很大的值。我们在计算第40个斐波那契数的时候第3个数重复计算了39088169次,第3个数被重复计算了这么多次,那第4 ,5,6等数也都会被重复计算很多次。这个程序的效率就会很低,因为重复计算的次数太多了。所以斐波那契数是不适合使用递归求解的,接下来试试非递归的求解。
3.2.2 迭代(非递归)求第n个斐波那契数
//非递归求第n个斐波那契数
#include <stdio.h>
int Fib(int n)
{
int a = 1;
int b = 1;
int c = 1;
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}
许多问题是以递归的形式进行解释的,这只是因为它比非递归的形式更为清晰。
但是这些问题的迭代实现往往比递归实现效率更高,虽然代码的可读性稍微差些。
当一个问题相当复杂,难以用迭代实现时,此时递归实现的简洁性便可以补偿它所带来的运行时开销
4.🌻补充练习
4.1 计算一个数的每位之和(递归实现)
示例:
写一个递归函数DigitSum(n),输入一个非负整数,返回组成它的数字之和。
示例:调用DigitSum(1729),则应该返回1+7+2+9,它的和是19
输入:1729
输出:19
思路:我们将1729的每一位拆出来
DigitSum(1729)
DigitSum(172)+9
DigitSum(17)+9+2
DigitSum(1)+7+9+2
//计算一个数的每位之和(递归实现)
#include <stdio.h>
int DigitSum(unsigned int n)
{
if (n < 10)
return n;
else
return DigitSum(n / 10) + n % 10;
}
int main()
{
unsigned int num = 0;
scanf("%u", &num);
int sum = DigitSum(num);
printf("%d\n", sum);
return 0;
}
4.2 写一个函数实现n的k次方(递归实现)
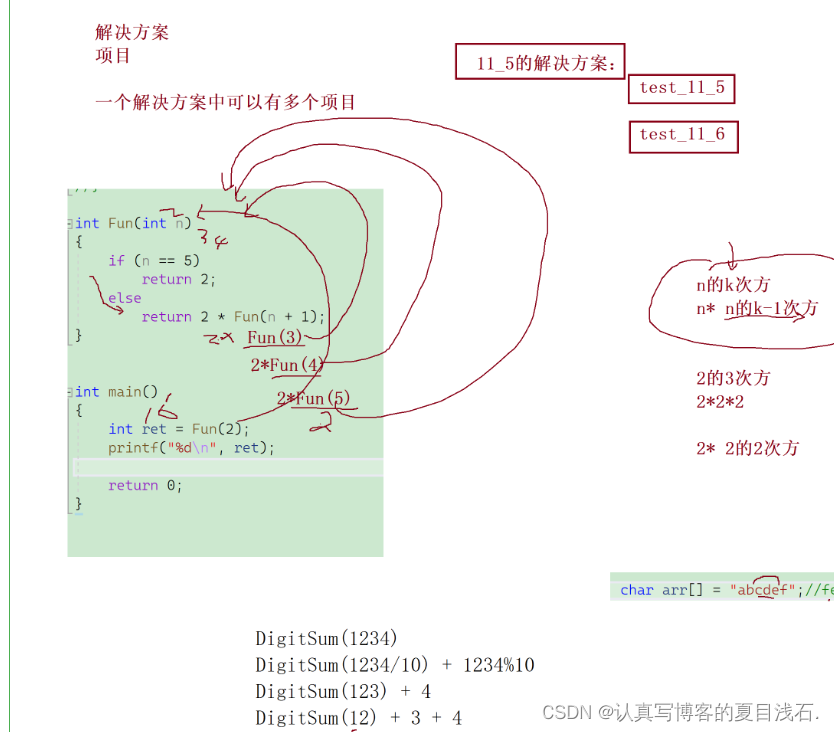
示例:
输入:2
输出 :8.000000
//递归实现n的k次方
#include <stdio.h>
double Pow(int n, int k)
{
if (k > 0)
return n * Pow(n, k - 1);
else if (k == 0)
return 1;
else
return 1.0 / Pow(n, -k);
//这种情况下返回的值是小数所以用double接收这个函数的返回值
}
int main()
{
int n = 0;
int k = 0;
scanf("%d %d", &n, &k);
double ret = Pow(n,k);
printf("%lf\n", ret);
return 0;
}
4.3 字符串逆序

编写一个函数 reverse_string(char * string)(递归实现)
实现:将参数字符串中的字符反向排列,不是逆序打印。
比如:
char arr[] = "abcdef";
逆序之后数组的内容变成:fedcba
4.3.1 非递归实现字符串逆序
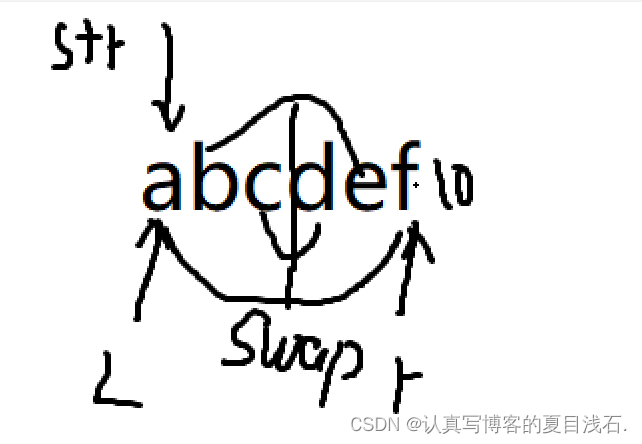
下标法思路:
- 数组arr[]=“abcdef”,我们发现逆序就是 a 和 f 交换,b 和 e 交换,c 和 d 交换,就是第一个字符和最后一个字符交换,第二个和倒数第二个交换,以此类推。
- 我们现在就是要找到他们就能进行交换了,我们给一个左边的下标 left = 0 给 a;给一个右下标 right = len-1 给 f。让左右下标锁定两个元素进行交换,交换完成后 left++,right- -,然后重新锁定新的元素进行交换,以此类推
//下标法
#include <stdio.h>
#include <string.h>
void reverse_string(char* str)
{
int len = strlen(str);
int left = 0;
int right = len - 1;
while (left < right)
{
char tmp = *(str + left);
*(str + left) = *(str + right);
*(str + right) = tmp;
left++;
right--;
}
}
int main()
{
char arr[] = "abcdef";
reverse_string(arr);
printf("%s\n", arr);//fedcba
return 0;
}
指针法思路:<指针法和下标法非常类似>
我们用一个 left 指针指向 a,用一个 right 指针指向 f ,然后再像前面下标法那样交换就可以了
//指针法
#include <stdio.h>
#include <string.h>
void reverse_string(char* str)
{
int len = strlen(str);
char* left = str;
char* right = str + len - 1;
while (left < right)
{
char tmp = *left;
*left = *right;
*right = tmp;
left++;
right--;
}
}
int main()
{
char arr[] = "abcdef";
reverse_string(arr);
printf("%s\n", arr);//fedcba
return 0;
}
补充:
strlen 是库函数,是计算字符串长度的,只针对字符串,关注 \0 的位置,\0 之前出现多少个字符,字符串的长度就是多少。
sizeof 是操作符,是计算数据占用内存空间的大小,单位是字节,不在乎内存中存放的是什么。
4.3.2 递归实现字符串逆序
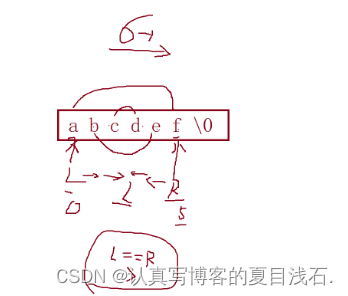
思路:把后面的字符赋值给前面的字符,后面的字符用\0覆盖
第一步:先创建一个变量tmp,将我们的 a 取出存放在 tmp 里面;
第二步:将后面的字符 f 存放在前面的字符 a 的位置(就是把 f 赋值给 a);
第三步:后面的字符 f 的位置用 \0 覆盖,然后逆序中间的字符 str+1 指向 b 的位置,逆序 bcde 字符;
第四步:将 tmp 中的 a 存放到后面字符的位置 上,以此类推。
//递归实现字符串逆序
#include <stdio.h>
int my_strlen(char* str)
{
int count = 0;
while (*str != '\0')
{
count++;
str++;
}
return count;
}
void reverse_string(char* str)
{
int len = my_strlen(str);
char tmp = *str;
*str = *(str + len - 1);
*(str + len - 1) = '\0';
if (my_strlen(str + 1) > 1)
reverse_string(str + 1);
*(str + len - 1) = tmp;
}
int main()
{
char arr[] = "abcdef";
reverse_string(arr);
printf("%s\n", arr);//fedcba
return 0;
}
🌺结语
蟹蟹大家看我的本篇博客,我是夏目浅石,我希望我们一起学习进步,刷题无数,咱们下期见。