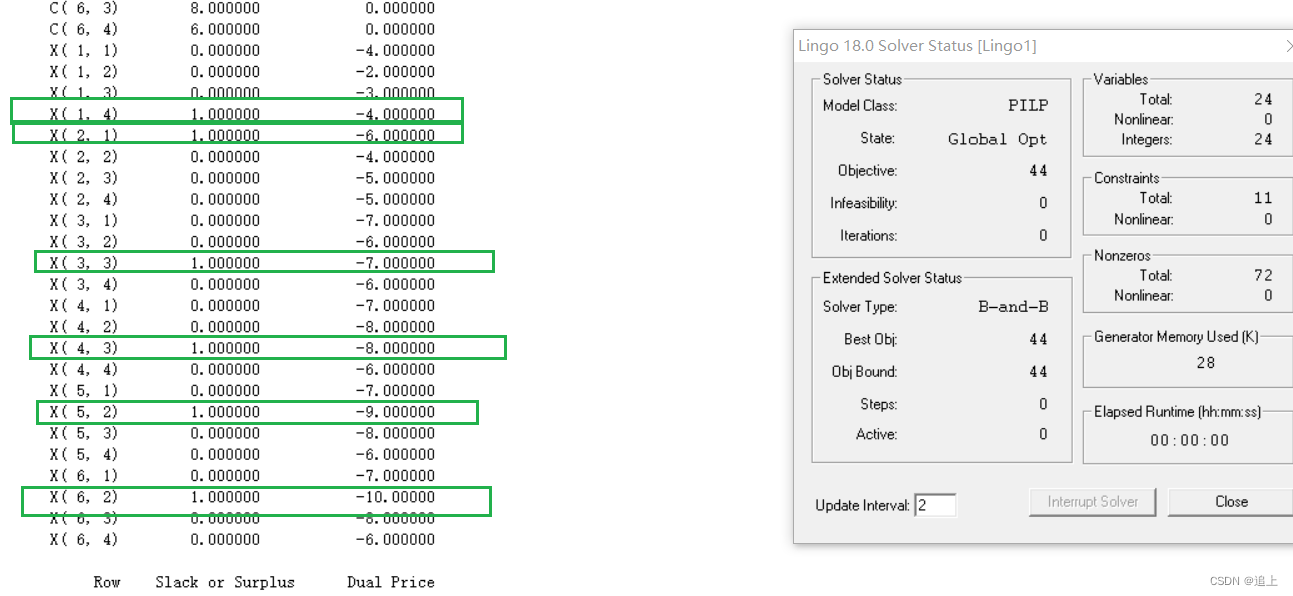
- 某公司新购置了某种设备 6 台,欲分配给下属的4 个企业,已知各企业获得这种设备后年创利润如表 1.1 所示,单位为千万元。问应如何分配这些设备能使年创总利润最大,最大利润是多少?
| 甲 | 乙 | 丙 | 丁 | |
|---|---|---|---|---|
| 1 | 4 | 2 | 3 | 4 |
| 2 | 6 | 4 | 5 | 5 |
| 3 | 7 | 6 | 7 | 6 |
| 4 | 7 | 8 | 8 | 6 |
| 5 | 7 | 9 | 8 | 6 |
| 6 | 7 | 10 | 8 | 6 |
甲公司2, 乙公5、6, 丙公司3、4,丁公司1,最大为44千万元
model:
sets:
goods/1..6/;
company/1..4/;
link(goods,company):c,x;
endsets
data:
c= 4 2 3 4
6 4 5 5
7 6 7 6
7 8 8 6
7 9 8 6
7 10 8 6;
enddata
Max=@sum(link:c*x);
@for(goods(i):@sum(company(j):x(i,j))=1);
@for(company(j):@sum(goods(i):x(i,j))<2);
@for(link:@bin(x));
end
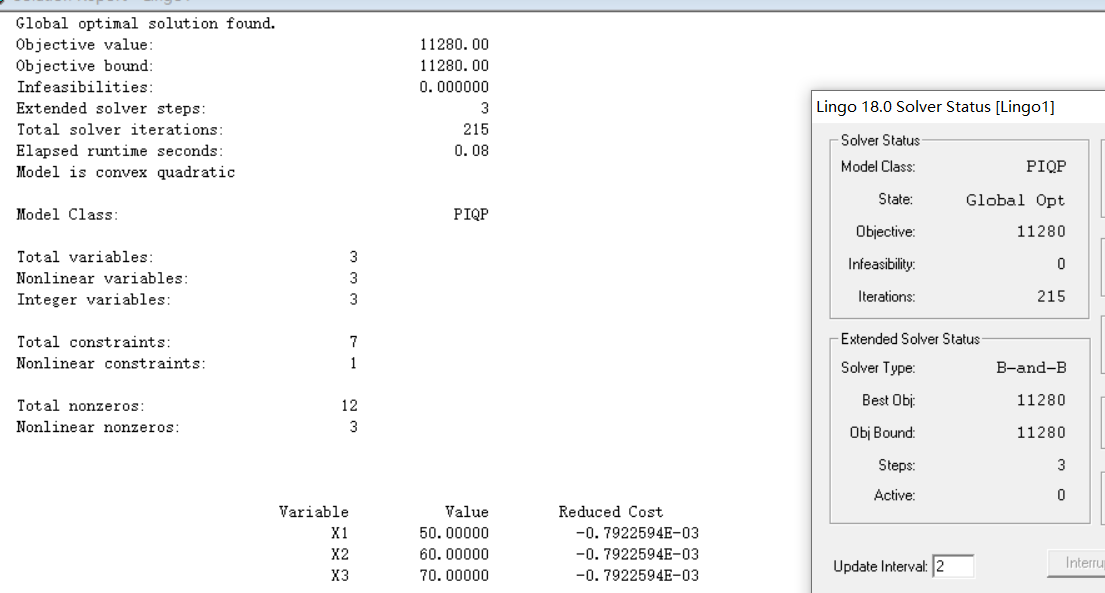
- 发动机最优生产计划模型求解。某工厂向用户提供发动机,按合同规定,其交货数量和日期是:第一季末交 40 台第二季末交 60 台,第三季末交 80 台。工厂的最大生产能力为每季 100 台,每季的生产费用是 50x + 0.2x2(元),此处 x为该季生产发动机的台数。若工厂生产得多,多余的发动机可移到下一季度向用户交货,此时工厂就需支付存储费,每台发动机每季的存储费为 4 元。问该厂每季应生产多少台发动机,才能既满足交货合同,又使工厂所花费的费用最少(假定第一季度无存货)?
MODEL:
min = 50*x1+0.2*x1*x1+(x1-40)*4+50*x2+0.2*x2*x2+(x1-40+x2-60)*4+50*x3+0.2*x3*x3;
x1 - 40 + x2 - 60 + x3 = 80;
x1 - 40 + x2 >= 60;
x1 >= 40;
x1 <= 100;
x2 <= 100;
x1 <= 100;
@gin(x1);@gin(x2);@gin(x3);
end
第一季度生产50台,第二季度生产60台,第三季度生产70台,总费用最小为11280元