生成树问题汇总

news2025/1/6 21:28:56

生成树问题汇总

  • 注
  • 1、最小(大)生成树
    • 思路
    • 代码
    • 例子：
      • 1、最小生成树结果是
      • 2、最大生成树结果
  • 2、在最小生成树中再加一条边，求新的最小生成树
    • 思路
    • 代码
      • 核心代码
      • 全部代码
    • 例子
  • 3、次小生成树
    • 思路:在上一个功能基础上进一步扩充
    • 代码
      • 核心代码
      • 全部代码
    • 例子
  • 4、判断最小生成树是否唯一
    • 思路
    • 代码
      • 核心代码
      • 全部代码
    • 例子
  • 5、极差(生成树：最长边-最短边)最小生成树
    • 思路
    • 代码
      • 核心代码
      • 完整代码
    • 例子

注

1、我们这里都采用kruskal算法，都使用邻接矩阵存储，这样是最方便的
2、生成树问题中，我们都认为图是：无向有权图
3、生成树，是在图的基础上完成的，虽然名字叫树，但本质上仍然是图，所以仍然用邻接矩阵存
4、完成生成树的问题时，必须要提前实现并查集，并查集是最基本的工具

1、一定记住，并查集序号是从1开始计算的
2、并查集详细解析见：第五章–二叉树 板子

class unions {
public:
	unions(int n) {//初始化
		this->n = n;
		for (int i = 0; i <= n; i++) {
			rank[i] = 0;
			father[i] = i;
		}
	}
	int find(int item) {
		//注意边界处理
		if (item > this->n || item <= 0) {
			return 0;
		}
		if (father[item] == item) {
			return item;
		}
		father[item] = find(father[item]);//路径压缩
		return father[item];
	}
	void merge(int x, int y) {
		link(find(x), find(y));
	}
private:
	int father[1000];//存爹数组
	int rank[1000];//秩
	int n;//规模
	void link(int x, int y) {//按秩合并
		if (rank[x] > rank[y]) {
			father[y] = x;
		}
		else {
			father[x] = y;
		}
		if (rank[x] == rank[y]) {
			rank[y]++;
		}
		return;
	}
};

1、最小(大)生成树

思路

基础算法：
1、给边按照升序(最小生成树)或者降序(最大生成树)排序
2、枚举所有边，如果边的端点属于不同的联通集合，那么该条边成功的连接了两者，合并进入并查集中
3、集合数为1时候，可以退出(但在实现时候没写，懒了，直接枚举所有边了，但这样不好)

代码

#include <iostream>
#include <string>
#include <stack>
#include <queue>
#include <unordered_map>
#include <vector>
#include <algorithm>
using namespace std;
class unions {//并查集
public:
	unions(int n) {
		this->n = n;
		for (int i = 0; i <= n; i++) {
			rank[i] = 0;
			father[i] = i;
		}
	}
	int find(int item) {
		//注意边界处理
		if (item > this->n || item <= 0) {
			return 0;
		}
		if (father[item] == item) {
			return item;
		}
		father[item] = find(father[item]);
		return father[item];
	}
	void merge(int x, int y) {
		link(find(x), find(y));
	}
private:
	int father[1000];
	int rank[1000];
	int n;
	void link(int x, int y) {
		if (rank[x] > rank[y]) {
			father[y] = x;
		}
		else {
			father[x] = y;
		}
		if (rank[x] == rank[y]) {
			rank[y]++;
		}
		return;
	}
};
//存储边的信息
struct Node_min {
	int x;
	int y;
	int dis;
	bool operator < (const Node_min & node) {
		//return dis > node.dis;//最大生成树，从大到小排序
		return dis < node.dis;//最小生成树，从小到大排序
	}
};
//所有示例的编号都从1开始
int minTree[100][100] = {};//存储生成树,都用邻接矩阵存储，方便
int n = 0;//全部的点数
int m = 0;//边数
int min_dis = 0;
vector<Node_min> edge;//存储全部边信息

//最小(大)生成树：kruskal算法
void function_one() {
	unions u(n);//一定看好点的编号，并查集从1开始
	int mins = 0;
	for (int i = 0; i < m; i++) {
		Node_min item = edge[i];
		if (u.find(item.x) != u.find(item.y)) {//只有新来的边的两个顶点，不在一个集合里，才能合并
			u.merge(item.x, item.y);//合并两个点
			cout << item.x << "-->" << item.y << endl;
			mins += item.dis;
			minTree[item.x][item.y] = item.dis;
			minTree[item.y][item.x] = item.dis;
		}
	}
	min_dis = mins;
	cout << min_dis << endl;//打印最小/最大权值
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}

int main()
{
	cin >> n >> m;
	edge.resize(m);//共m条边
	for (int i = 0; i < m; i++) {
		cin >> edge[i].x >> edge[i].y >> edge[i].dis;
	}
	sort(edge.begin(), edge.end());//按照边长排序

	cout << "开始构造最小(大)生成树" << endl;
	function_one();
	
	return 0;
}

例子：

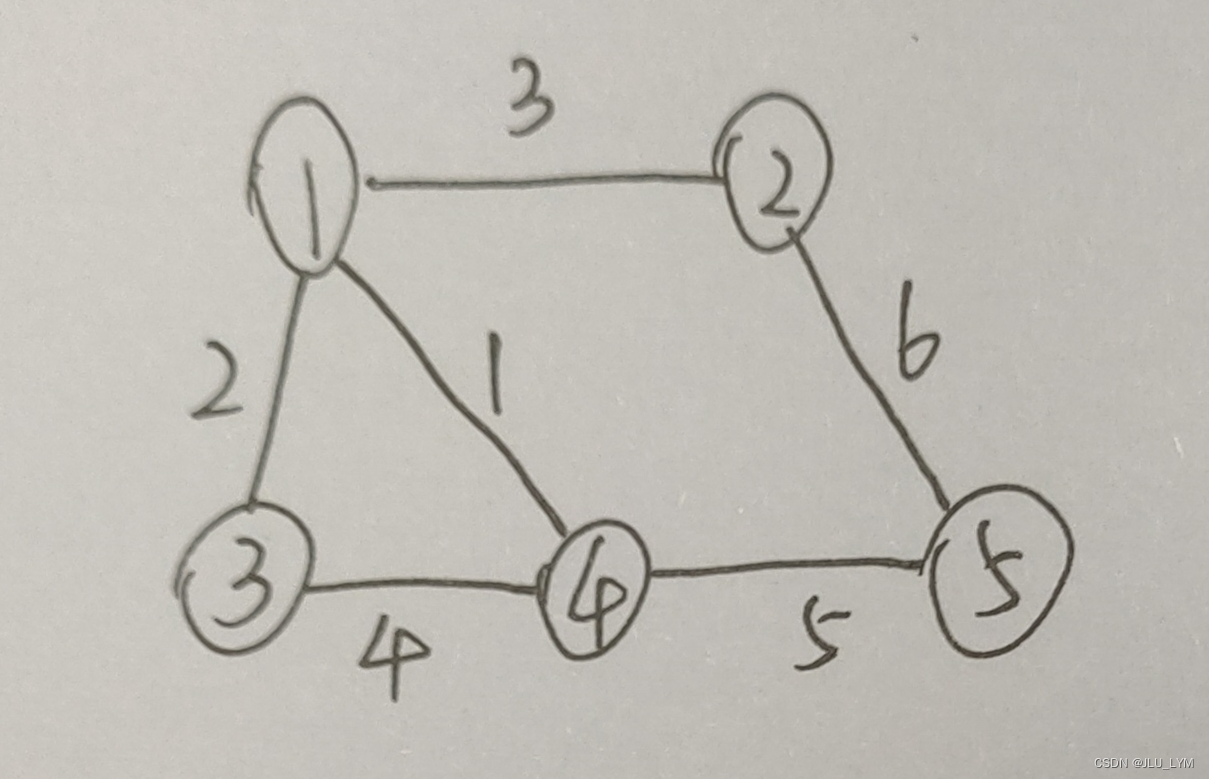
在这里插入图片描述

1、最小生成树结果是

在这里插入图片描述
程序输出：
在这里插入图片描述

2、最大生成树结果

在这里插入图片描述
在这里插入图片描述

2、在最小生成树中再加一条边，求新的最小生成树

思路

在a—b之间(二者在原最小生成树中未必直接相连)加一条边
1、必会产生环路。
2、在原最小生成树中，找a和b之间的，最长边(dfs函数)
3、新加的边>=最长边，则属于无效添加边，最小生成树不变；反之，替换掉最长边，这样，生成树权值进一步减少，成为新的最小生成树

代码

注:
1、先产生，最小生成树，在执行添加边操作
2、最小生成树中，到达任何一个点都是唯一路径的，所以到达之后，直接做标记即可

核心代码

int s1 = 0, e1 = 0;//全局变量带出最大值对应边的端点(起点、终点)
void dfs(int v, int b, bool visit[], int crew, int s, int e, int* ans) {//参数：当前点，目标点，辅助遍历数组，辅助记录当前最大值，辅助记录最大值边端点，用于带出最大值
	visit[v] = true;
	if (v == b) {//因为最小生成树没有环路，所以只可能是单一路径到这里，所以到这里就截止即可，看最大值
		*(ans) = crew;//crew就是在a-->b遍历途中，不断访问可以访问的点，在所有边中找到最大值，给他带出去
		s1 = s;//带出对应边端点
		e1 = e;
		return;
	}
	for (int i = 1; i <= n; i++) {
		if (minTree[v][i] != 0 && !visit[i]) {//枚举所有可到达的，并且没访问的点
			int tmp = crew, s0 = s, e0 = e;//记录本函数原始的数值
			//之后过程：对于当前要走的点，看看能否更新最大值，再dfs，再恢复，为下一次做准备
			if (minTree[v][i] > crew) {//发现一条边权值更大
				crew = minTree[v][i];//更新
				s = v;
				e = i;
			}
			dfs(i, b, visit, crew, s, e, ans);
			//往这个点走已经走完，所以要继续往别的点走，数据恢复到初始状态，准备走下一次(回溯想法)
			crew = tmp;
			s = s0;
			e = e0;
		}
	}
}
void function_two() {
	int a = 0, b = 0, newe = 0;
	cin >> a >> b >> newe;//从a到b，权值是newe
	bool visit[1000];
	for (int i = 0; i < n; i++) {//n为全局变量，记录总点数
		visit[i] = false;
	}
	int ans = 0;//记录a-->b最长的边
	dfs(a, b, visit, 0, 1, 1, &ans);
	cout << "a-->b之间最长边是从" << s1 << "-->" << e1 << "长度是" << ans << endl;
	if (ans <= newe) {
		cout << "输入的新边大于a-->b的最长边，所以原最小生成树不变" << endl;
	}
	else {
		cout << "输入的新边小于于a-->b的最长边，所以原最小生成树改变" << endl;
		minTree[s1][e1] = 0;
		minTree[e1][s1] = 0;//最长边删除
		minTree[a][b] = newe;
		minTree[b][a] = newe;//把新的边加进来
	}
	for (int i = 1; i <= n; i++) {//打印生成树
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}

全部代码

#include <iostream>
#include <string>
#include <stack>
#include <queue>
#include <unordered_map>
#include <vector>
#include <algorithm>
using namespace std;

//并查集(作为工具类使用)
class unions {
public:
	unions(int n) {
		this->n = n;
		for (int i = 0; i <= n; i++) {
			rank[i] = 0;
			father[i] = i;
		}
	}
	int find(int item) {
		//注意边界处理
		if (item > this->n || item <= 0) {
			return 0;
		}
		if (father[item] == item) {
			return item;
		}
		father[item] = find(father[item]);
		return father[item];
	}
	void merge(int x, int y) {
		link(find(x), find(y));
	}
private:
	int father[1000];
	int rank[1000];
	int n;
	void link(int x, int y) {
		if (rank[x] > rank[y]) {
			father[y] = x;
		}
		else {
			father[x] = y;
		}
		if (rank[x] == rank[y]) {
			rank[y]++;
		}
		return;
	}
};

//存储边的信息
struct Node_min {
	int x;
	int y;
	int dis;
	bool operator < (const Node_min & node) {
		return dis < node.dis;//最小生成树，从小到大排序
	}
};
//最小(大)生成树：kruskal算法
void function_one() {
	unions u(n);//一定看好点的编号，并查集从1开始
	int mins = 0;
	for (int i = 0; i < m; i++) {
		Node_min item = edge[i];
		if (u.find(item.x) != u.find(item.y)) {//只有新来的边的两个顶点，不在一个集合里，才能合并
			u.merge(item.x, item.y);//合并两个点
			cout << item.x << "-->" << item.y << endl;
			mins += item.dis;
			minTree[item.x][item.y] = item.dis;
			minTree[item.y][item.x] = item.dis;
		}
	}
	min_dis = mins;
	cout << min_dis << endl;//打印最小/最大权值
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}

//开始添加边并且调整生成树
int s1 = 0, e1 = 0;//全局变量带出最大值对应边的端点
void dfs(int v, int b, bool visit[], int crew, int s, int e, int* ans) {//参数：当前点，目标点，辅助遍历数组，辅助记录当前最大值，辅助记录最大值边端点，用于带出最大值
	visit[v] = true;
	if (v == b) {//因为最小生成树没有环路，所以只可能是单一路径到这里，所以到这里就截止即可，看最大值
		*(ans) = crew;//crew就是在a-->b遍历途中，不断访问可以访问的点，在所有边中找到最大值，给他带出去
		s1 = s;
		e1 = e;
		return;
	}
	for (int i = 1; i <= n; i++) {
		if (minTree[v][i] != 0 && !visit[i]) {
			int tmp = crew, s0 = s, e0 = e;
			if (minTree[v][i] > crew) {
				crew = minTree[v][i];
				s = v;
				e = i;
			}
			dfs(i, b, visit, crew, s, e, ans);
			//往这个点走已经走完，所以要继续往别的点走，数据恢复到初始状态，准备走下一次(回溯想法)
			crew = tmp;
			s = s0;
			e = e0;
		}
	}
}
void function_two() {
	int a = 0, b = 0, newe = 0;
	cin >> a >> b >> newe;
	bool visit[1000];
	for (int i = 0; i < n; i++) {//n为全局变量，记录总点数
		visit[i] = false;
	}
	int ans = 0;//记录a-->b最长的边
	dfs(a, b, visit, 0, 1, 1, &ans);
	cout << "a-->b之间最长边是从" << s1 << "-->" << e1 << "长度是" << ans << endl;
	if (ans <= newe) {
		cout << "输入的新边大于a-->b的最长边，所以原最小生成树不变" << endl;
	}
	else {
		cout << "输入的新边小于于a-->b的最长边，所以原最小生成树改变" << endl;
		minTree[s1][e1] = 0;
		minTree[e1][s1] = 0;//最长边删除
		minTree[a][b] = newe;
		minTree[b][a] = newe;//把新的边加进来
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}
int main()
{
	cin >> n >> m;
	edge.resize(m);//共m条边
	for (int i = 0; i < m; i++) {
		cin >> edge[i].x >> edge[i].y >> edge[i].dis;
	}
	sort(edge.begin(), edge.end());//按照边长，从小到大排序

	cout << "开始构造最小(大)生成树" << endl;
	function_one();
	cout << "开始加入一条新的边" << endl;
	function_two();
	return 0;
}

例子

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3、次小生成树

思路:在上一个功能基础上进一步扩充

1、枚举所有未加入的边，动态维护哪一条边加入之后，新的生成树权值最小，就是答案
2、在原图之上加入一条新的边(新的边一定加进来)，必定会产生环路，必须要删去原图中一条边，因为求得是第二小生成树，删去原图之中在这两个目标点之间最长的边，这样新的边对权值的增量最小，所以，找最长边函数和"图中加入新边"那个递归函数一致
3、新的生成树权值=原来的最小值-找到的最长边长+欲加入的边的长度

代码

核心代码

int s1 = 0, e1 = 0;//全局变量带出最大值对应边的端点(起点、终点)
void dfs(int v, int b, bool visit[], int crew, int s, int e, int* ans) {//参数：当前点，目标点，辅助遍历数组，辅助记录当前最大值，辅助记录最大值边端点，用于带出最大值
	visit[v] = true;
	if (v == b) {//因为最小生成树没有环路，所以只可能是单一路径到这里，所以到这里就截止即可，看最大值
		*(ans) = crew;//crew就是在a-->b遍历途中，不断访问可以访问的点，在所有边中找到最大值，给他带出去
		s1 = s;//带出对应边端点
		e1 = e;
		return;
	}
	for (int i = 1; i <= n; i++) {
		if (minTree[v][i] != 0 && !visit[i]) {//枚举所有可到达的，并且没访问的点
			int tmp = crew, s0 = s, e0 = e;//记录本函数原始的数值
			//之后过程：对于当前要走的点，看看能否更新最大值，再dfs，再恢复，为下一次做准备
			if (minTree[v][i] > crew) {//发现一条边权值更大
				crew = minTree[v][i];//更新
				s = v;
				e = i;
			}
			dfs(i, b, visit, crew, s, e, ans);
			//往这个点走已经走完，所以要继续往别的点走，数据恢复到初始状态，准备走下一次(回溯想法)
			crew = tmp;
			s = s0;
			e = e0;
		}
	}
}
//生成次小生成树
void function_three() {
	int sec_min = 9999;//新的权值，以下三行都是动态维护
	int s2 = 0, e2 = 0, dis2 = 0;//新加入的边的 起点终点
	int s0 = 0, e0 = 0;//要删除的原最小生成树边
	for (int i = 0; i < m; i++) {//枚举边
		bool visit[1000] = { false };//辅助数组
		if (minTree[edge[i].x][edge[i].y] == 0) {//说明这条边没进入最小生成树中，是潜在的可能的构成次小生成树的边
			int tmp_maxs = 0;//在edge[i].x和edge[i].y之间的最长边长，被edge[i].dis所替换
			dfs(edge[i].x, edge[i].y, visit, 0, 0, 0, &tmp_maxs);
			if (min_dis - tmp_maxs + edge[i].dis < sec_min) {//在所有这种生成树中动态找到最小值，即为答案
				sec_min = min_dis - tmp_maxs + edge[i].dis;
				s0 = s1, e0 = e1;//s1 e1 全局变量带出最大值(tmp_maxs)对应边的端点
				s2 = edge[i].x, e2 = edge[i].y, dis2 = edge[i].dis;
			}
		}
	}
	
	cout << "次小生成树的的值是" << sec_min << endl;
	minTree[s0][e0] = 0;
	minTree[e0][s0] = 0;//删除一条边边
	minTree[s2][e2] = dis2;
	minTree[e2][s2] = dis2;//把新的边加进来
	cout << "次小生成树：" << endl;
	for (int i = 1; i <= n; i++) {//打印生成树
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}

全部代码

#include <iostream>
#include <string>
#include <stack>
#include <queue>
#include <unordered_map>
#include <vector>
#include <algorithm>
using namespace std;

//并查集(作为工具类使用)
class unions {
public:
	unions(int n) {
		this->n = n;
		for (int i = 0; i <= n; i++) {
			rank[i] = 0;
			father[i] = i;
		}
	}
	int find(int item) {
		//注意边界处理
		if (item > this->n || item <= 0) {
			return 0;
		}
		if (father[item] == item) {
			return item;
		}
		father[item] = find(father[item]);
		return father[item];
	}
	void merge(int x, int y) {
		link(find(x), find(y));
	}
private:
	int father[1000];
	int rank[1000];
	int n;
	void link(int x, int y) {
		if (rank[x] > rank[y]) {
			father[y] = x;
		}
		else {
			father[x] = y;
		}
		if (rank[x] == rank[y]) {
			rank[y]++;
		}
		return;
	}
};

//存储边的信息
struct Node_min {
	int x;
	int y;
	int dis;
	bool operator < (const Node_min & node) {
		return dis < node.dis;//最小生成树，从小到大排序
	}
};
//最小(大)生成树：kruskal算法
void function_one() {
	unions u(n);//一定看好点的编号，并查集从1开始
	int mins = 0;
	for (int i = 0; i < m; i++) {
		Node_min item = edge[i];
		if (u.find(item.x) != u.find(item.y)) {//只有新来的边的两个顶点，不在一个集合里，才能合并
			u.merge(item.x, item.y);//合并两个点
			cout << item.x << "-->" << item.y << endl;
			mins += item.dis;
			minTree[item.x][item.y] = item.dis;
			minTree[item.y][item.x] = item.dis;
		}
	}
	min_dis = mins;
	cout << min_dis << endl;//打印最小/最大权值
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}

//开始添加边并且调整生成树
int s1 = 0, e1 = 0;//全局变量带出最大值对应边的端点
void dfs(int v, int b, bool visit[], int crew, int s, int e, int* ans) {//参数：当前点，目标点，辅助遍历数组，辅助记录当前最大值，辅助记录最大值边端点，用于带出最大值
	visit[v] = true;
	if (v == b) {//因为最小生成树没有环路，所以只可能是单一路径到这里，所以到这里就截止即可，看最大值
		*(ans) = crew;//crew就是在a-->b遍历途中，不断访问可以访问的点，在所有边中找到最大值，给他带出去
		s1 = s;
		e1 = e;
		return;
	}
	for (int i = 1; i <= n; i++) {
		if (minTree[v][i] != 0 && !visit[i]) {
			int tmp = crew, s0 = s, e0 = e;
			if (minTree[v][i] > crew) {
				crew = minTree[v][i];
				s = v;
				e = i;
			}
			dfs(i, b, visit, crew, s, e, ans);
			//往这个点走已经走完，所以要继续往别的点走，数据恢复到初始状态，准备走下一次(回溯想法)
			crew = tmp;
			s = s0;
			e = e0;
		}
	}
}
//生成次小生成树
void function_three() {
	int sec_min = 9999;//新的权值，以下三行都是动态维护
	int s2 = 0, e2 = 0, dis2 = 0;//新加入的边的 起点终点
	int s0 = 0, e0 = 0;//要删除的原最小生成树边
	for (int i = 0; i < m; i++) {
		bool visit[1000] = { false };//辅助数组
		if (minTree[edge[i].x][edge[i].y] == 0) {//说明这条边没进入最小生成树中，是潜在的可能的构成次小生成树的边
			int tmp_maxs = 0;//在edge[i].x和edge[i].y之间的最长边长，被edge[i].dis所替换
			dfs(edge[i].x, edge[i].y, visit, 0, 0, 0, &tmp_maxs);
			if (min_dis - tmp_maxs + edge[i].dis < sec_min) {//在所有这种生成树中动态找到最小值，即为答案
				sec_min = min_dis - tmp_maxs + edge[i].dis;
				s0 = s1, e0 = e1;//s1 e1 全局变量带出最大值(tmp_maxs)对应边的端点
				s2 = edge[i].x, e2 = edge[i].y, dis2 = edge[i].dis;
			}
		}
	}
	cout << "次小生成树的的值是" << sec_min << endl;
	minTree[s0][e0] = 0;
	minTree[e0][s0] = 0;//删除一条边边
	minTree[s2][e2] = dis2;
	minTree[e2][s2] = dis2;//把新的边加进来
	cout << "次小生成树：" << endl;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}
int main()
{
	cin >> n >> m;
	edge.resize(m);//共m条边
	for (int i = 0; i < m; i++) {
		cin >> edge[i].x >> edge[i].y >> edge[i].dis;
	}
	sort(edge.begin(), edge.end());//按照边长，从小到大排序

	cout << "开始构造最小(大)生成树" << endl;
	function_one();
	cout << "开始构建次小生成树" << endl;
	function_three();
	
	return 0;
}

例子

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4、判断最小生成树是否唯一

思路

1、kruskal算法基础之上
2、两条权值一样的边(边的两个端点分属于不同的连通分量才有讨论意义)
3、二者能够连接相同的两个连通块，说明二者谁进入最小生成树都行，就不唯一
4、注意一下
在这里插入图片描述

代码

核心代码

void function_four() {
	unions u(n);
	for (int i = 0; i < m; i++) {
		Node_min tmp = edge[i];
		if (u.find(tmp.x) == u.find(tmp.y)) {//只有该条边的端点分属于两个不同联通集团时候，才有判断价值
			continue;
		}
		int j = i + 1;
		while (j < m) {//从他之后找权值和他一样的边，看端点所属的连通分量是否一致
			if (edge[j].dis != tmp.dis) {//权值不一样不考虑
				break;
			}
			//这里一定要找全了，我们找的是两个联通的集团，没有固定对应关系
			if ((u.find(tmp.x) == u.find(edge[j].x) && u.find(tmp.y) == u.find(edge[j].y)) || (u.find(tmp.x) == u.find(edge[j].y) && u.find(tmp.y) == u.find(edge[j].x))) {
				cout << "最小生成树不唯一";
				cout << "边" << tmp.x << "--" << tmp.y << "和边" << edge[j].x << "--" << edge[j].y << "可任意选择" << endl;
				return;
			}
			j++;
		}
		u.merge(tmp.x, tmp.y);
	}
	cout << "最小生成树唯一";
	return;
}

全部代码

#include <iostream>
#include <string>
#include <stack>
#include <queue>
#include <unordered_map>
#include <vector>
#include <algorithm>
using namespace std;

//并查集(作为工具类使用)
class unions {
public:
	unions(int n) {
		this->n = n;
		for (int i = 0; i <= n; i++) {
			rank[i] = 0;
			father[i] = i;
		}
	}
	int find(int item) {
		//注意边界处理
		if (item > this->n || item <= 0) {
			return 0;
		}
		if (father[item] == item) {
			return item;
		}
		father[item] = find(father[item]);
		return father[item];
	}
	void merge(int x, int y) {
		link(find(x), find(y));
	}
private:
	int father[1000];
	int rank[1000];
	int n;
	void link(int x, int y) {
		if (rank[x] > rank[y]) {
			father[y] = x;
		}
		else {
			father[x] = y;
		}
		if (rank[x] == rank[y]) {
			rank[y]++;
		}
		return;
	}
};

//存储边的信息
struct Node_min {
	int x;
	int y;
	int dis;
	bool operator < (const Node_min & node) {
		return dis < node.dis;//最小生成树，从小到大排序
	}
};
//最小(大)生成树：kruskal算法
void function_one() {
	unions u(n);//一定看好点的编号，并查集从1开始
	int mins = 0;
	for (int i = 0; i < m; i++) {
		Node_min item = edge[i];
		if (u.find(item.x) != u.find(item.y)) {//只有新来的边的两个顶点，不在一个集合里，才能合并
			u.merge(item.x, item.y);//合并两个点
			cout << item.x << "-->" << item.y << endl;
			mins += item.dis;
			minTree[item.x][item.y] = item.dis;
			minTree[item.y][item.x] = item.dis;
		}
	}
	min_dis = mins;
	cout << min_dis << endl;//打印最小/最大权值
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << minTree[i][j] << ' ';
		}
		cout << endl;
	}
	return;
}
//判断是否唯一
void function_four() {
	unions u(n);
	for (int i = 0; i < m; i++) {
		Node_min tmp = edge[i];
		if (u.find(tmp.x) == u.find(tmp.y)) {//只有该条边的端点分属于两个不同联通集团时候，才有判断价值
			continue;
		}
		int j = i + 1;
		while (j < m) {
			if (edge[j].dis != tmp.dis) {//权值不一样不考虑
				break;
			}
			//这里一定要找全了，我们找的是两个联通的集团，没有固定对应关系
			if ((u.find(tmp.x) == u.find(edge[j].x) && u.find(tmp.y) == u.find(edge[j].y)) || (u.find(tmp.x) == u.find(edge[j].y) && u.find(tmp.y) == u.find(edge[j].x))) {
				cout << "最小生成树不唯一";
				cout << "边" << tmp.x << "--" << tmp.y << "和边" << edge[j].x << "--" << edge[j].y << "可任意选择" << endl;
				return;
			}
			j++;
		}
		u.merge(tmp.x, tmp.y);
	}
	cout << "最小生成树唯一";
	return;
}
int main()
{
	cin >> n >> m;
	edge.resize(m);//共m条边
	for (int i = 0; i < m; i++) {
		cin >> edge[i].x >> edge[i].y >> edge[i].dis;
	}
	sort(edge.begin(), edge.end());//按照边长，从小到大排序

	cout << "开始构造最小(大)生成树" << endl;
	function_one();
	cout << "开始判断最小生成树是否唯一" << endl;
	function_four();
	
	return 0;
}

例子

在这里插入图片描述
在这里插入图片描述

5、极差(生成树：最长边-最短边)最小生成树

在这里插入图片描述
在这里插入图片描述

思路

1、极差：生成树中，最长边-最小边，所有生成树中，找这个值的最小值
2、他也是生成树问题，在考研的范围之内，直接使用类似于kruskal算法(从最小的边开始枚举，最后一个加入的边一定是最长的)+控制变量法(控制最短边，从头开始枚举最短边，最后一条边一定最长)
3、需要把边从小到大排序，传统的kruskal算法是构建以dis最小的边为最短边的最小生成树(这句话就是，枚举边的时候，从哪里开始，kruskal算法就是从头开始)
4、但是本算法需要极差最小，只从头开始枚举最短边很明显不够
5、所以从头枚举最短边执行kruskal算法(就是从头开始依次建立最小生成树)，建立完成获得极差，直到从某一个点开始建立最小生成树失败，全停止，所有的极差中获取最小值
6、这样也相当于控制了最短边这个变量，使计算过程简化

代码

核心代码

void function_five() {
	int ans = 99999;//记录最小极差
	for (int i = 0; i < m; i++) {//外层循环，枚举最短边(以不同最短边分别进行建立最小生成树)

		unions u(n);//本次建立最小生成树所用的并查集

		Node_min item = edge[i];
		cout << "以" << item.x << "--" << item.y << "为最短边的最小生成树" << endl;
		int gap = item.dis;//用来计算极差，item.dis是最短边，相当于控制变量，控制最小值的边，找到最大值的边(最后一个进入最小生成树中的边)，算极差

		int sets = n;//集合数
		int val = 0;//最小生成树权值
		for (int j = i; j < m; j++) {
			Node_min tmp = edge[j];
			if (u.find(tmp.x) != u.find(tmp.y)) {
				cout << tmp.x << "--" << tmp.y << ' ';
				u.merge(tmp.x, tmp.y);
				val += tmp.dis;
				sets--;
				if (sets == 1) {//集合数为1，说明最后一条最大边进来，生成树建立完毕，如果退出时都不为1，说明建立失败
					gap = tmp.dis - gap;//这也是为什么用kruskal算法原因，控制最短边，只要能生成最小生成树 ，最后一条边，一定是最大边，以最快速度计算出极差
					break;
				}
			}
		}
		if (sets > 1) {//生成树构造失败：未能吧所有的点连接到一起(一个集合里面去)
			cout << endl;
			cout << "构造失败，停止全部构造" << endl;//只要这个失败了，后面不肯能还有成功的
			break;
		}
		else {
			cout << endl;
			cout << "该最小生成树权值：" << val << "极差是" << gap << endl;
			ans = min(ans, gap);
		}
	}
	cout << "极差最小生成树的极差是" << ans << endl;
	return;
}

完整代码

#include <iostream>
#include <string>
#include <stack>
#include <queue>
#include <unordered_map>
#include <vector>
#include <algorithm>
using namespace std;

//并查集(作为工具类使用)
class unions {
public:
	unions(int n) {
		this->n = n;
		for (int i = 0; i <= n; i++) {
			rank[i] = 0;
			father[i] = i;
		}
	}
	int find(int item) {
		//注意边界处理
		if (item > this->n || item <= 0) {
			return 0;
		}
		if (father[item] == item) {
			return item;
		}
		father[item] = find(father[item]);
		return father[item];
	}
	void merge(int x, int y) {
		link(find(x), find(y));
	}
private:
	int father[1000];
	int rank[1000];
	int n;
	void link(int x, int y) {
		if (rank[x] > rank[y]) {
			father[y] = x;
		}
		else {
			father[x] = y;
		}
		if (rank[x] == rank[y]) {
			rank[y]++;
		}
		return;
	}
};

//存储边的信息
struct Node_min {
	int x;
	int y;
	int dis;
	bool operator < (const Node_min & node) {
		return dis < node.dis;//最小生成树，从小到大排序
	}
};
//开始判定极差最小生成树
void function_five() {
	int ans = 99999;//记录最小极差
	for (int i = 0; i < m; i++) {//外层循环，枚举最短边(以不同最短边分别进行建立最小生成树)

		unions u(n);//本次建立最小生成树所用的并查集

		Node_min item = edge[i];
		cout << "以" << item.x << "--" << item.y << "为最短边的最小生成树" << endl;
		int gap = item.dis;//用来计算极差，item.dis是最短边，相当于控制变量，控制最小值的边，找到最大值的边，算极差

		int sets = n;//集合数
		int val = 0;//最小生成树权值
		for (int j = i; j < m; j++) {
			Node_min tmp = edge[j];
			if (u.find(tmp.x) != u.find(tmp.y)) {
				cout << tmp.x << "--" << tmp.y << ' ';
				u.merge(tmp.x, tmp.y);
				val += tmp.dis;
				sets--;
				if (sets == 1) {
					gap = tmp.dis - gap;//这也是为什么用kruskal算法原因，控制最短边，只要能生成最小生成树 ，最后一条边，一定是最大边，以最快速度计算出极差
					break;
				}
			}
		}
		if (sets > 1) {//生成树构造失败：未能吧所有的点连接到一起(一个集合里面去)
			cout << endl;
			cout << "构造失败，停止全部构造" << endl;//只要这个失败了，后面不肯能还有成功的
			break;
		}
		else {
			cout << endl;
			cout << "该最小生成树权值：" << val << "极差是" << gap << endl;
			ans = min(ans, gap);
		}
	}
	cout << "极差最小生成树的极差是" << ans << endl;
	return;
}
int main()
{
	cin >> n >> m;
	edge.resize(m);//共m条边
	for (int i = 0; i < m; i++) {
		cin >> edge[i].x >> edge[i].y >> edge[i].dis;
	}
	sort(edge.begin(), edge.end());//按照边长，从小到大排序
	
	cout << "开始构造极差最小的生成树" << endl;
	function_five();

	return 0;
}

例子

在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/75602.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

一个轻量级的分布式日志标记追踪神器，十分钟接入，非常好用！

一个轻量级的分布式日志标记追踪神器，十分钟接入，非常好用！

TLog简介 1、TLog通过对日志打标签完成企业级微服务的日志追踪。它不收集日志&#xff0c;使用简单&#xff0c; 产生全局唯一的追踪码。除了追踪码以外&#xff0c;TLog还支持SpanId和上下游服务信息 标签的追加。 2、为用户使用方便而设计&#xff0c;提供完全零侵入式接入…
阅读更多...
es入门（上）

es入门（上）

笔记来源于学习 b站中的【IT李老师】的elasticsearch课程 自己在实习做的es模块中的理解。 后续会有 中&#xff0c;下篇笔记更新&#xff0c;目前这一篇是上篇。 目录 Elastic Stack简介 1.1简介 1.2特色 1.3组件介绍 2.Elasticsearch的接收与核心概念 2.1搜索是什么…
阅读更多...
【Keras+计算机视觉+Tensorflow】OCR文字识别实战（附源码和数据集 超详细必看）

【Keras+计算机视觉+Tensorflow】OCR文字识别实战（附源码和数据集 超详细必看）

需要源码和数据集请点赞关注收藏后评论区留言私信~~~ 一、OCR文字识别简介 利用计算机自动识别字符的技术&#xff0c;是模式识别应用的一个重要领域。人们在生产和生活中&#xff0c;要处理大量的文字、报表和文本。为了减轻人们的劳动&#xff0c;提高处理效率&#xff0c;从…
阅读更多...
[python]初步练习脚本

[python]初步练习脚本

之前练习的python&#xff0c;编写的脚本&#xff0c;现在作为记录&#xff0c;方便查看~ python 初步练习脚本基础部分的练习脚本脚本代码1、helloworld.py&#xff0c;有for循环语句2、main.py3、range—test.py&#xff0c;范围4、RE.py&#xff0c;花式输出内容5、turtle练…
阅读更多...
Jekins安装和部署

Jekins安装和部署

1.官网下载 注意jekins各版本不同支持jdk的版本也不同 https://www.jenkins.io/download/ 如图进去后可看见最新版&#xff0c;而past releases是历史版本 查看自己各版本的支持 我下载的是2.346.1版本&#xff0c;是war包形式 2.启动jekins 直接在war包路径 java命令启动…
阅读更多...
lspci命令整理

lspci命令整理

1. 作用&#xff1a; 显示当前主机的所有PCI总线信息 2. 常用指令&#xff1a; lspci -nn 第一列的数字&#xff1a;总线编号(Bus Number)&#xff1a;设备编号&#xff08;Device Number&#xff09;&#xff1a;功能编号&#xff08;Function Number&#xff09; 第一个中括…
阅读更多...
全国青少年软件编程等级考试C语言标准解读(1_10级)

全国青少年软件编程等级考试C语言标准解读(1_10级)

考试性质 全国青少年软件编程等级考试标准&#xff08;C/C&#xff09;由中国电子学会科普培训与应用推广中心指定。由全国青少年电子信息科普创新联盟标准工作组开发&#xff0c;由中国电子学会普及工作委员会审核通过&#xff0c;适用于由中国电子学会主办的青少年软件编程等…
阅读更多...
vue中的process.env的理解

vue中的process.env的理解

创建项目的时候突然发现好多前端有好多地方用到了这个process.env.xxxx但是发现其实我的新项目并没有定义这个内容&#xff0c;于是就对这个变量产生了好奇&#xff0c;这里总结一下 上图是我在node命令行下执行的查看了一下变量&#xff0c;看这情况直接是把系统的环境变量给…
阅读更多...
少走弯路，关于在线客服系统的二三事

少走弯路，关于在线客服系统的二三事

日常生活中&#xff0c;我们购买一个服务或一个商品时&#xff0c;时常会遇到以下场景&#xff1a; 售前咨询&#xff1a;向商家咨询服务的信息咨询、商品的规格产品咨询、以及商场活动、优惠咨询等 售后服务&#xff1a;商品使用问题、商品不满意退/换货等 在移动通信没有普…
阅读更多...
Camera Surface 从应用到cameraserver的流转

Camera Surface 从应用到cameraserver的流转

一、Android相机应用与Surface Camera应用的预览一般通过SurfaceView去显示&#xff0c;SurfaceView作为显示的载体&#xff0c; Surface surface mSurfaceView.getSurfaceHolder().getSurface(); 获取的surface会通过Camera API1/API2的接口下发到framework层&#xff1b;…
阅读更多...
基于模型的设计（MBD）在汽车ECU软件开发中的实践

基于模型的设计（MBD）在汽车ECU软件开发中的实践

基于模型的设计&#xff08;Model-based Design&#xff0c;以下简称MBD&#xff09;是一种围绕模型展开的项目开发方法&#xff0c;指对开发对象或者项目产品进行精确建模&#xff0c;项目的需求分析、功能设计、系统框架、代码生成、测试验证等开发环节都在模型的基础上展开。…
阅读更多...
如何用策略模式，优化你代码里的的if-else？

如何用策略模式，优化你代码里的的if-else？

最近有一个学妹在跟我沟通如何有效的去避免代码中一长串的if else判断或者switch条件判断&#xff1f;针对更多的回答就是合理的去使用设计来规避这个问题。 在设计模式中&#xff0c;可以使用工厂模式或者策略模式来处理这类问题&#xff0c;之前已经分享了工厂模式&#xff…
阅读更多...
Hadoop集群中HDFS的API测试案例以及MapReduce的多种提交Job方式案例

Hadoop集群中HDFS的API测试案例以及MapReduce的多种提交Job方式案例

这两个案例默认是hadoop集群环境已经搭建好以及IDEA环境也已经配置好 1、HDFS客户端测试案例 1.1、pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www…
阅读更多...
Java使用ftl模板文件生成Word，以及Word转换图片或Pdf工具类

Java使用ftl模板文件生成Word，以及Word转换图片或Pdf工具类

Java使用ftl模板文件生成Word 一、写在前面 最近在项目中使用打印功能&#xff0c;发现这个功能我已经写过多次了&#xff0c;下面这个文章的发步日期在2020年&#xff0c;不得不感慨时间之快啊。 https://blog.csdn.net/weixin_43238452/article/details/109636200?spm1001…
阅读更多...
this关键字，是如何把你难倒的？

this关键字，是如何把你难倒的？

作为一名实战前端工程师&#xff0c;在jq时代&#xff0c;是经常被this关键字难倒的。几年前每次我意识到程序出现问题的时候&#xff0c;都本能反应是自己的this没有绑定好&#xff0c;于是重新绑定一下&#xff0c;就能解决了。但是他确实一直为难着我。 转眼到了2022年底&a…
阅读更多...
图解LeetCode——1780. 判断一个数字是否可以表示成三的幂的和（难度：中等）

图解LeetCode——1780. 判断一个数字是否可以表示成三的幂的和（难度：中等）

一、题目 给你一个整数 n &#xff0c;如果你可以将 n 表示成若干个不同的三的幂之和&#xff0c;请你返回 true &#xff0c;否则请返回 false 。 对于一个整数 y &#xff0c;如果存在整数 x 满足 y 3^x &#xff0c;我们称这个整数 y 是三的幂。 二、示例 2.1> 示例…
阅读更多...
SpringBoot面试杀手锏——自动配置原理

SpringBoot面试杀手锏——自动配置原理

引言 不论在工作中&#xff0c;亦或是求职面试&#xff0c;Spring Boot已经成为我们必知必会的技能项。除了某些老旧的政府项目或金融项目持有观望态度外&#xff0c;如今的各行各业都在飞速的拥抱这个已经不是很新的Spring启动框架。 当然&#xff0c;作为Spring Boot的精髓…
阅读更多...
凌恩客户文章|JCR 一区:多组学联合分析揭示PCOS真元凶

凌恩客户文章|JCR 一区:多组学联合分析揭示PCOS真元凶

期刊&#xff1a;Journal of Ovarian Research 影响因子&#xff1a;5.506 发表时间&#xff1a;2022年10月 客户单位&#xff1a;汕头大学医学院第一附属医院鄞国书课题组 一、研究背景 多囊卵巢综合征(PCOS)是导致育龄妇女不孕的最常见内分泌疾病…
阅读更多...
MyBatis二 MyBatis常见面试题

MyBatis二 MyBatis常见面试题

一 MyBatis是什么&#xff1f; MyBatis是一款优秀的持久层框架&#xff0c;一个半ORM &#xff08;对象关系映射&#xff09;框架&#xff0c;它支持定制化SQL、存储过程以及高级映射。MyBatis避免了几乎所有的JDBC代码和手动设置参数以及获取结果集。MyBatis可以使用简单的XM…
阅读更多...
postman+newman+jenkins持续集成

postman+newman+jenkins持续集成

今天为大家带来的是postmannewmanjenkins进行API接口测试的持续集成: 一. postman测试实战 postman测试API接口是通过JavaScript脚本完成测试中的功能, 在请求发起前后实现测试操作. 常用功能: 请求前脚本(pre-request scripts)设置请求前置操作如设置变量等 请求后在tests…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023