目录
- 第三节 函数的连续性
- (1)函数的连续性
- 例1(补充定义,函数连续)
- 例4(无穷小*有界量)
- 例6 (补充定义,三角函数的代换的妙用)
- (2)连续函数的运算和初等函数的连续性
- 1. 连续函数的运算
- 2. 初等函数的连续性
- 例7(结论)
- 例8(只有洛必达时才需要n化成x)
- 例10(初等函数秒杀)
- 例11
- 例14(绝对值)
- 例17
- (3)间断点及其分类
- 1. 间断点的定义
- 2. 间断点的分类
- 例20
- 例21
- 例22
- 例23
- 例25
- 补充:天生的间断点
- (4)闭区间上连续函数的性质(重要)
- 零点定理
- 例28(注意一定要说连续,这是基础)
- 例31 (公式证明 函数连续就该想到:最值介值有界零点)
- 介值定理的推广(用介值和最值推理)
- 例34 (积分中值定理的一般形式的证明)
- 总结
第三节 函数的连续性
(1)函数的连续性



左端点右连续,右端点左连续,则()变为【】
例1(补充定义,函数连续)

有理化 洛必达 等价
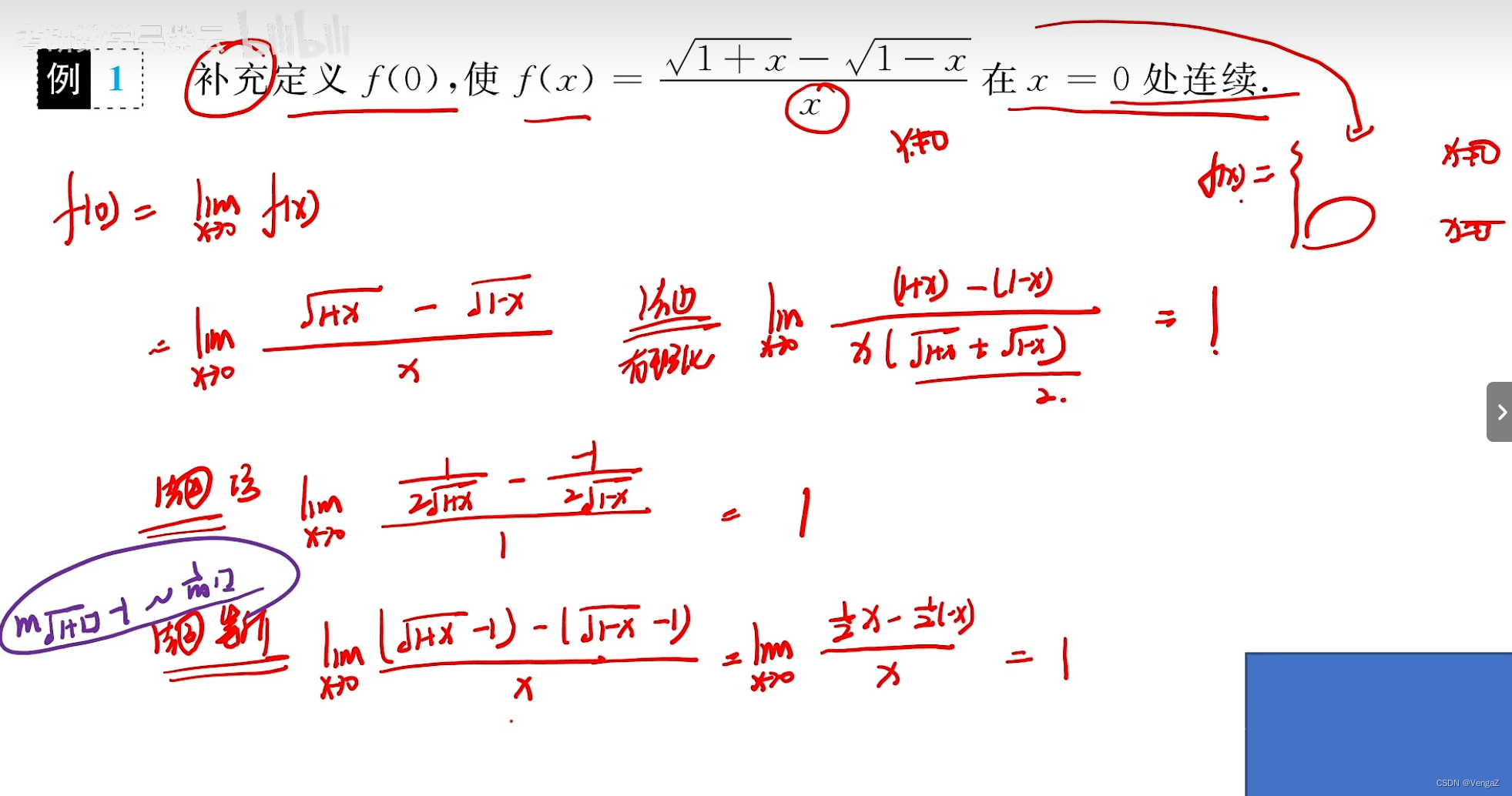
例4(无穷小*有界量)

趋于0的大于0次方等于无穷小,趋于0的小于等于0次方,不等于无穷小
例6 (补充定义,三角函数的代换的妙用)
开区间的补充

(2)连续函数的运算和初等函数的连续性
1. 连续函数的运算
有限次的四则运算或者复合运算之后还是连续

单调函数必为反函数,反函数不一定是单调函数
2. 初等函数的连续性
初等函数是基本初等函数经过有限次四则或者复合的函数

例7(结论)


例8(只有洛必达时才需要n化成x)

例10(初等函数秒杀)

例11

例14(绝对值)


中括号的部分可以考虑已经是连续,只需要考虑中括号没有包含的部分
例17

(3)间断点及其分类
1. 间断点的定义

2. 间断点的分类


例20


例21

例22

例23

例25


反例法(取恒等常数)

补充:天生的间断点
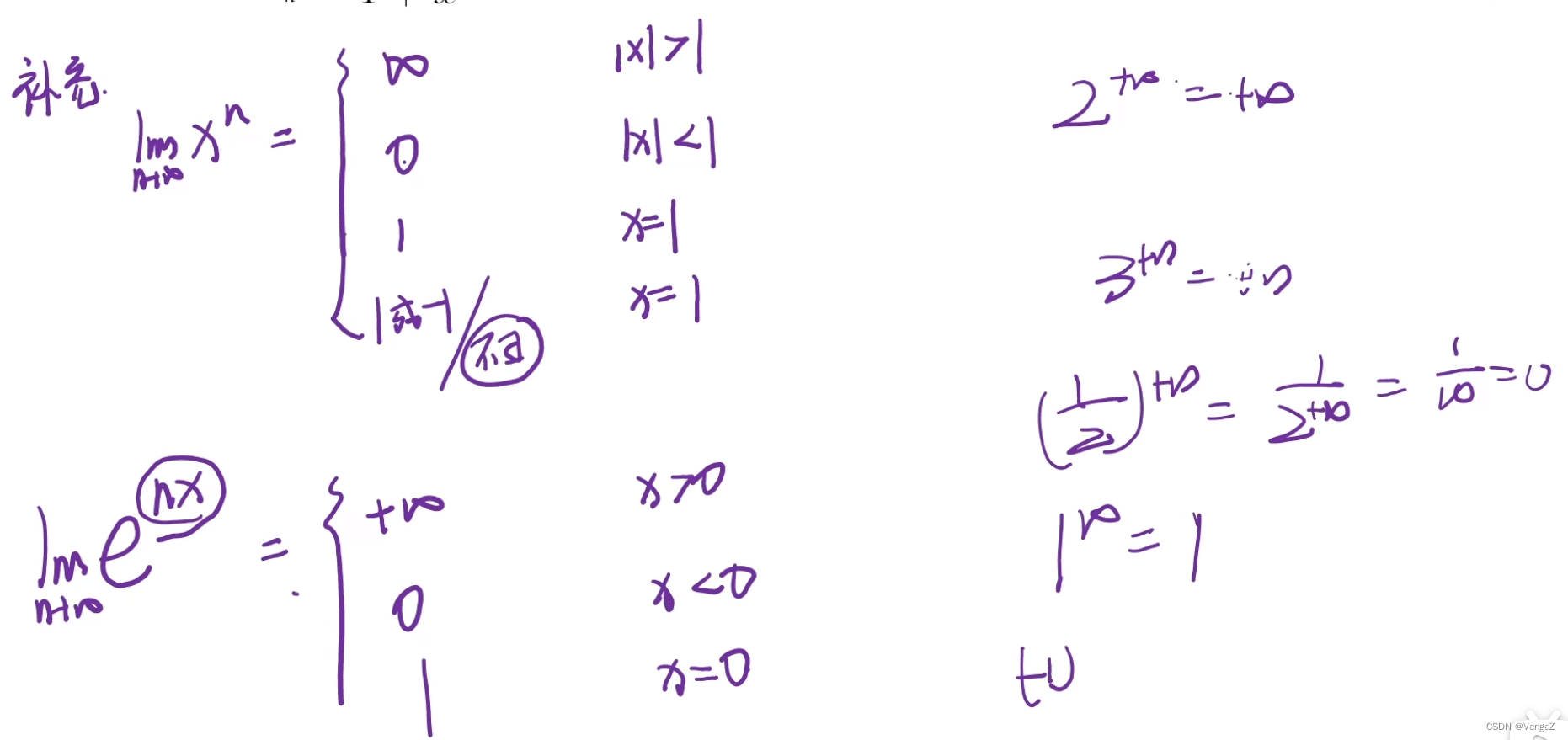
(4)闭区间上连续函数的性质(重要)

对于开区间以及闭区间,如果取值是闭区间则取值范围也是闭区间
零点定理

例28(注意一定要说连续,这是基础)

端点等号的情况得单独说
例31 (公式证明 函数连续就该想到:最值介值有界零点)
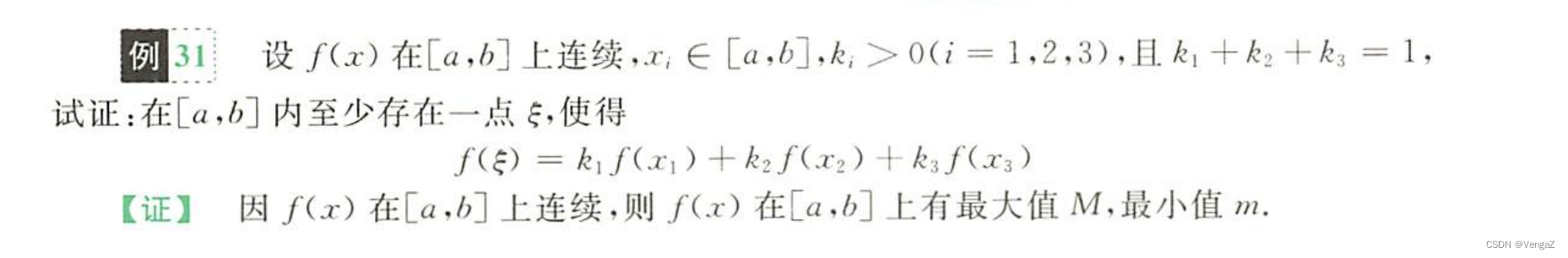
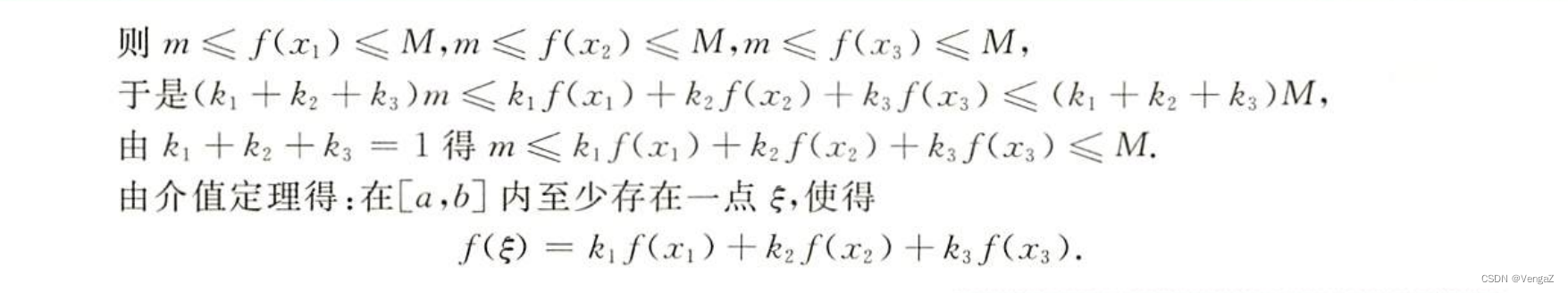
介值定理就是连续并且取值范围内,则存在点等于
例33类似

介值定理的推广(用介值和最值推理)

端点等号的情况得单独说
例34 (积分中值定理的一般形式的证明)
积分中值定理还有加强形式,由拉格朗日证明
此一般形式由介值和最值定理证明

总结
函数的连续性和间断点是在数学中研究函数性质和行为时经常讨论的概念。
连续性是指函数在某一点或某个区间上的无间断性质。具体来说,一个函数在某点x=a处连续,意味着在该点的左右两侧函数值存在极限,并且这两个极限相等,即lim(x→a-) f(x) = lim(x→a+) f(x) = f(a)。这表示函数在点a处没有跳跃、断裂或间断现象,图像可以被画出而不需要提笔。如果函数在整个定义域内的每个点都满足连续性,那么它被称为连续函数。
间断点是指函数在某点或某些点处不满足连续性的点。间断点可以分为三种类型:
-
可去间断点(Removable Discontinuity):在可去间断点处,函数在该点左右两侧的极限存在,但函数在该点处的值与极限不相等。这种间断点可以通过修正函数在该点的定义来移除,使得函数在该点处连续。
-
跳跃间断点(Jump Discontinuity):在跳跃间断点处,函数在该点左右两侧的极限存在,但左右两侧的极限不相等。函数在该点处的值会出现跃变,图像在该点处存在一个跳跃。
-
无穷间断点(Infinite Discontinuity):在无穷间断点处,函数在该点左右两侧的极限至少有一个趋于无穷大或负无穷大。这种间断点表示函数在该点处的值无法定义或者发散到无穷。
间断点的存在导致函数在这些点处无法保持连续性,而具体的间断类型取决于函数在该点的极限情况。在研究函数的性质和行为时,对于连续性和间断点的理解和分析是非常重要的。