实验四：最小生成树

一、实验目的：

理解最小生成树的画法。提高学生编写实验报告，总结实验结果的能力，培养学生的逻辑思维能力和算法设计思想。能够独立完成简单的算法设计和分析，进一步用他们来解决实际问题，帮助学生学习掌握C和C++语言程序设计的基本方法和各种调试手段，使学生具备程序设计的能力。

二、实验内容：

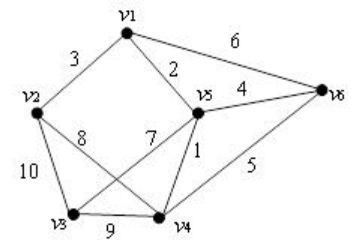
给定一个带权图，求其最小生成树

三、实验原理

避圈法或破圈法

四、程序代码与实验结果

在这里插入图片描述

#include <iostream>
#include <vector>
#include <limits>

using namespace std;

const int MAX = 100;
const int INF = numeric_limits<int>::max();  // 定义 INF 为 int 类型的最大值
vector<vector<int>> result(MAX,vector<int>(2,0));

// prim 算法函数，计算最小生成树的权值并返回
int prim(vector<vector<int>> &graph) {
    int n = graph.size();  // 获取图中节点数
    vector<bool> visited(n, false);  // 标记节点是否已被访问过
    vector<int> minDist(n, INF);  // 记录节点到最小生成树的最短距离
    vector<int> parent(n, -1);  // 记录节点在最小生成树中的父节点
    minDist[0] = 0;  // 从第 0 个节点开始，到自身的距离为 0
    int res = 0;  // 最小生成树的权值

    for (int i = 0; i < n; ++i) {  // 进行 n 次遍历，每次加入一个节点
        int u = -1;  // 记录当前未访问节点中，距离最小生成树最近的节点
        for (int j = 0; j < n; ++j) {  // 寻找未访问节点中距离最小生成树最近的节点
            if (!visited[j] && (u == -1 || minDist[j] < minDist[u])) {
                u = j;
            }
        }
        cout<<"最小生成树各边如下："<<endl;

        visited[u] = true;  // 标记该节点已被访问
        if (parent[u] != -1) {  // 输出加入最小生成树的边的权值和信息
            result[i-1][0] = parent[u]+1;
            result[i-1][1] = u+1;
            cout << parent[u] + 1 << "-" << u + 1 << ":" << minDist[u] << endl;
        }
        res += minDist[u];  // 将该节点到最小生成树的最短距离加入最小生成树的权值中

        for (int v = 0; v < n; ++v) {  // 更新未被访问节点到最小生成树的最短距离
            if (!visited[v] && graph[u][v] < minDist[v]) {
                minDist[v] = graph[u][v];
                parent[v] = u;  // 记录 v 在最小生成树中的父节点为 u
            }
        }
    }

    return res;  // 返回最小生成树的权值
}

int main() {
    // 定义邻接矩阵表示的图
    /*
     vector<vector<int>> graph = {
        {0, 1, 2, INF, INF},
        {1, 0, 4, 2, INF},
        {2, 4, 0, 3, 5},
        {INF, 2, 3, 0, 1},
        {INF, INF, 5, 1, 0}
    };

    */
    vector<vector<int>> graph(7, vector<int>(7, INF));

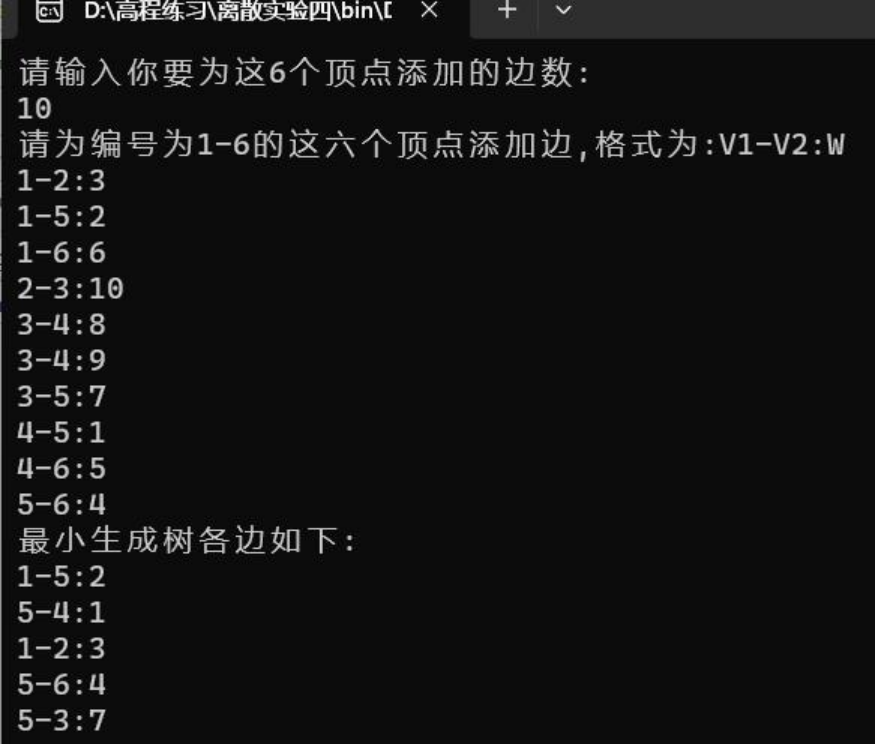
    cout<<"请输入你要为这6个顶点添加的边数："<<endl;
    int n;
    cin>>n;
    cout<< "请为编号为1-6的这六个顶点添加边，格式为：V1-V2:W" <<endl;
    int a,b,w;

    for(int i = 1; i <= n; i++){
         scanf("%d-%d:%d",&a,&b,&w);
         graph[a-1][b-1] = graph[b-1][a-1] = w;
    }



    // 输出最小生成树的权值
   prim(graph);


    return 0;
}