1可选实验室: 特征缩放和学习率(多变量)
1.1 目标
在这个实验室里:
- 利用前一实验室开发的多变量线性回归模型程序
- 在具有多种功能的数据集上运行梯度下降法
- 探讨学习速度 alpha 对梯度下降法的影响
- 通过使用 z 分数标准化的特征缩放来提高梯度下降法的性能
1.2 工具
您将使用在上一个实验中开发的函数以及matplotlib和NumPy。
import numpy as np
np.set_printoptions(precision=2)
import matplotlib.pyplot as plt
dlblue = '#0096ff'; dlorange = '#FF9300'; dldarkred='#C00000'; dlmagenta='#FF40FF'; dlpurple='#7030A0';
plt.style.use('./deeplearning.mplstyle')
from lab_utils_multi import load_house_data, compute_cost, run_gradient_descent
from lab_utils_multi import norm_plot, plt_contour_multi, plt_equal_scale, plot_cost_i_w1.3 表示法

2 问题陈述
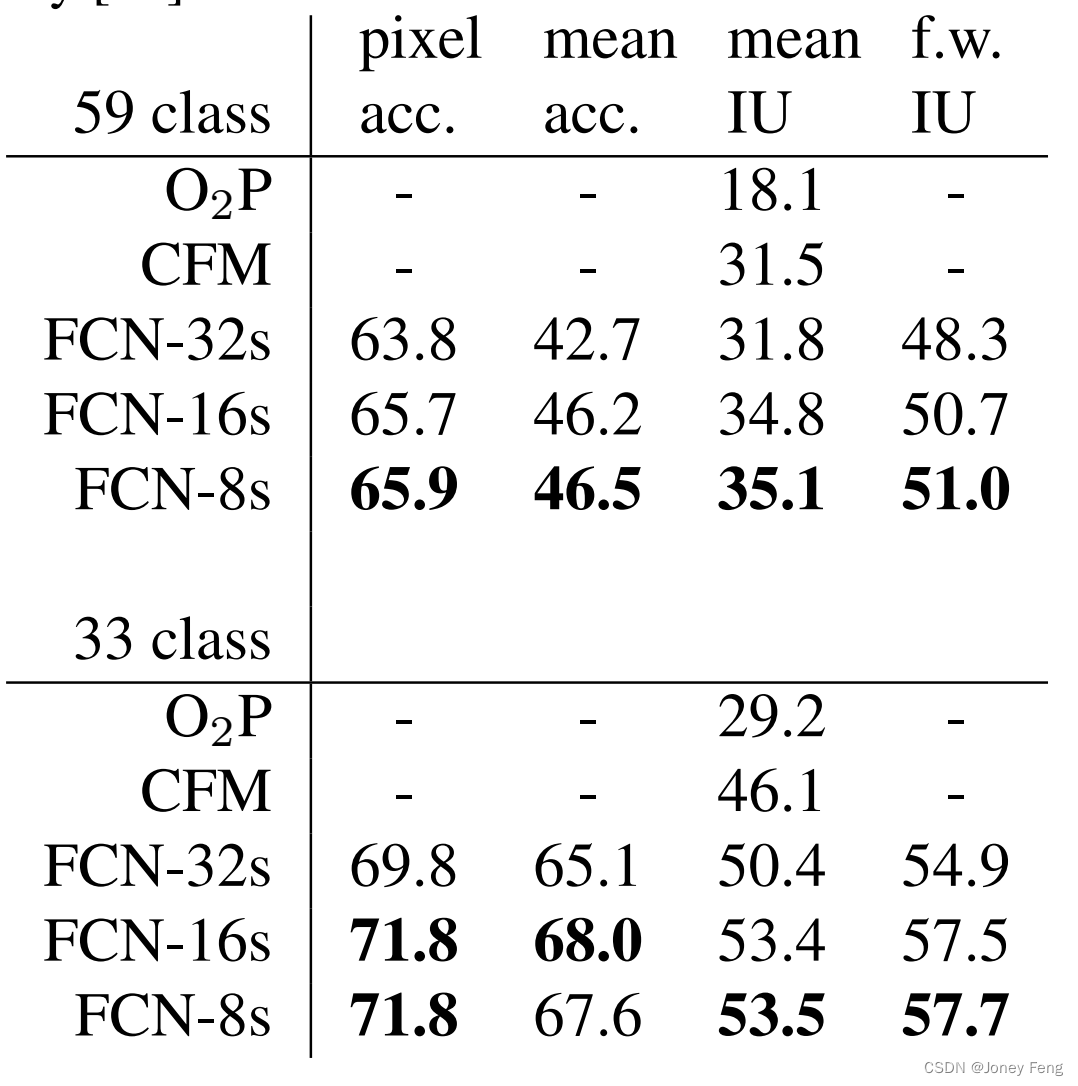
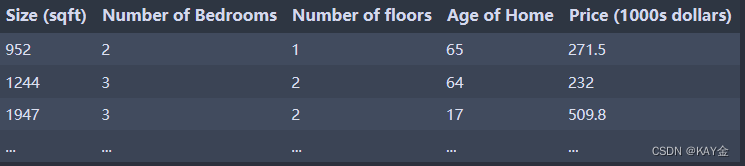
与前面的实验一样,您将使用房价预测的激励实例。培训数据集包含许多示例,其中4个特征(大小、卧室、楼层和年龄)如下表所示。注意,在这个实验室中,尺寸特性是在平方英尺,而早期的实验室使用1000平方英尺。这个数据集比以前的实验室大。
我们希望利用这些价值建立一个线性回归模型,这样我们就可以预测其他房子的价格——比如,一套1200平方英尺、3间卧室、1层楼、40年历史的房子。
2.1 数据集
# load the dataset
X_train, y_train = load_house_data()
X_features = ['size(sqft)','bedrooms','floors','age']
fig,ax=plt.subplots(1, 4, figsize=(12, 3), sharey=True)
for i in range(len(ax)):
ax[i].scatter(X_train[:,i],y_train)
ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("Price (1000's)")
plt.show()让我们通过绘制每个特征与价格的关系来查看数据集及其特征。
输出为:
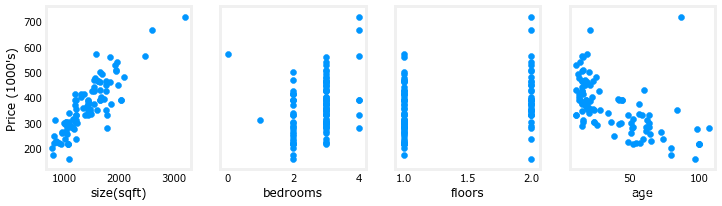
绘制每个特性与目标价格的对比图,可以提供一些指示,说明哪些特性对价格的影响最大。可以看出,增加规模也会增加价格。卧室和地板似乎对房价没有太大影响。较新的房子比较旧的房子有更高的价格。
2.2 梯度下降法多变量
下面是你在上一个实验室里开发的多变量梯度下降法方程:

其中,n 是特性的数量,参数 wj,b,同时更新

m是数据集中训练例子的数量。fw,b (x (i))是模型的预测值,而 y (i)是目标值。
2.3 学习率

讲座讨论了一些与设置学习速率 α 有关的问题。学习速率控制参数更新的大小。见上方程式(1)。它由所有参数共享。
让我们运行梯度下降法并尝试一些 α 设置在我们的数据集上。
2.3.1 𝛼= 9.9e-7
#set alpha to 9.9e-7
_, _, hist = run_gradient_descent(X_train, y_train, 10, alpha = 9.9e-7)
输出:
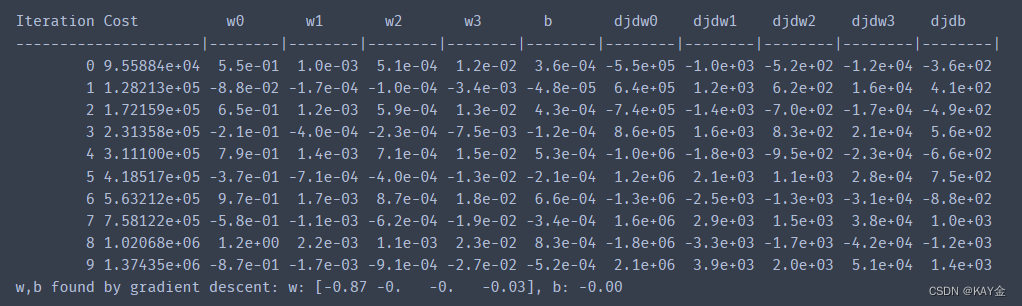
看来学习速度太快了。解不会收敛。成本不降反升。
让我们描绘一下结果:
plot_cost_i_w(X_train, y_train, hist) 输出:
右边的图显示了其中一个参数 w0的值
.在每次迭代中,它都超出了最优值,结果是成本最终增加而不是接近最小值。请注意,这不是一个完全准确的图片,因为有4个参数被修改,而不是只有一个。此图仅显示 w0,其他参数固定为良性值。在本图和后面的图中,你可能会注意到蓝色和橙色的线条有些偏离。
2.3.2 𝛼= 9e-7
让我们尝试一个小一点的值,看看会发生什么。
#set alpha to 9e-7
_,_,hist = run_gradient_descent(X_train, y_train, 10, alpha = 9e-7)
plot_cost_i_w(X_train, y_train, hist)输出:
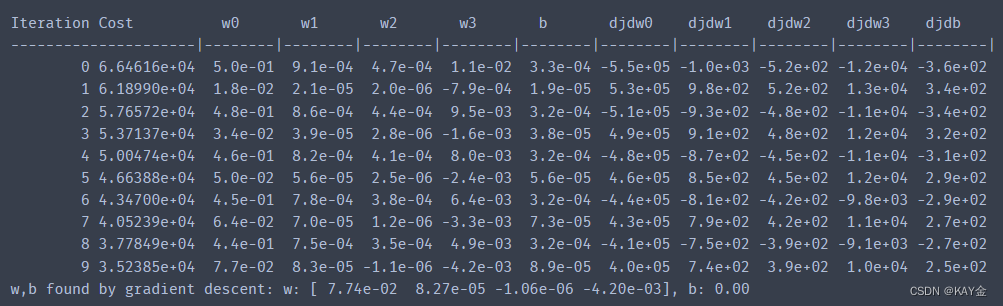
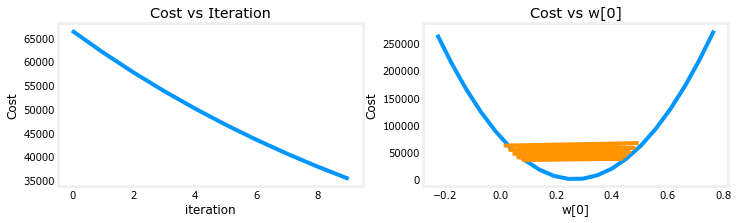
成本在整个运行过程中不断下降,表明 alpha 不是太大。
在左边,您可以看到成本正在减少。在右边,你可以看到 w0仍然围绕最小值振荡,但是它在减少而不是增加每次迭代。上面注意,当 w [0]跳过最佳值时,dj _ dw [0]每次迭代都改变符号。这个 alpha 值将会收敛。您可以改变迭代次数,以查看它的行为。
2.3.3 𝛼= 1e-7
让我们试试小一点的 α 值,看看会发生什么。
#set alpha to 1e-7
_,_,hist = run_gradient_descent(X_train, y_train, 10, alpha = 1e-7)
plot_cost_i_w(X_train,y_train,hist)输出:


成本在整个运行过程中不断下降,表明 α 不是太大。
在左边,您可以看到成本正在减少,因为它应该这样做。在右边你可以看到 w0正在减少,但是没有越过最小值。注意上面的 dj _ w0在整个运行过程中都是负的。这个解决方案也会收敛,尽管不像前面的例子那么快。
2.4 特征缩放

讲座描述了重新缩放数据集的重要性,使特征具有相似的范围。如果你对为什么会出现这种情况的细节感兴趣,请点击下面的“细节”标题。如果没有,下面的部分将介绍如何进行特性扩展的实现。
让我们再来看看 α = 9e-7的情况。这非常接近我们可以不发散地设置 α 的最大值。这是显示最初几个迭代的短暂过程:

以上,虽然成本正在下降,很明显,w0比其他参数进展更快,因为它的梯度大得多。
下图显示了使用 α= 9e-7进行长时间运行的结果。这需要几个小时。

以上,你可以看到成本降低后,其最初的减少缓慢。注意 w0和 w0、 w1、 w2以及 dj _ dw0和 dj _ dw1-3之间的区别。W0很快达到接近最终值,dj _ dw0很快降低到一个很小的值,表明 w0接近最终值。其他参数的降低要慢得多。
为什么会这样? 有什么我们可以改进的吗? 看下面:

上图显示了为什么更新得不均匀。
- α由所有参数更新(w 和 b)共享
- 常见误差项乘以 w 的特征(不是 b)
- 这些特性的数量级差异很大,使得一些特性的更新速度比其他特性快得多。在这种情况下,w0乘以“ size (sqft)”,通常大于1000,而 w1乘以“ number of bedrooms”,通常是2-4。
解决方案是特征缩放。
讲座讨论了三种不同的技巧:
- 特性缩放,本质上是将每个特性除以用户选择的值,得到 -1到1之间的范围。
- 平均标准化: xi: = (xi-μi)/(max-min)
- Z 分数标准化,我们将在下面探讨。
2.4.1 Z-分数正规化
在 z 分数标准化后,所有特性的平均值为0,标准差为1。
要实现 z 分数标准化,调整输入值,如下公式所示:

其中 j 选择 X 矩阵中的一个特征或列。μj 是特征(j)所有值的平均值,σj 是特征(j)的标准差。

实现注意: 当标准化功能时,存储用于标准化的值很重要——平均值和用于计算的标准差。在学习了模型中的参数之后,我们通常想要预测我们从未见过的房子的价格。给定一个新的 x 值(客厅面积和卧室数量) ,我们必须首先使用先前从训练集中计算出的平均值和标准差对 x 进行标准化。
def zscore_normalize_features(X):
"""
computes X, zcore normalized by column
Args:
X (ndarray): Shape (m,n) input data, m examples, n features
Returns:
X_norm (ndarray): Shape (m,n) input normalized by column
mu (ndarray): Shape (n,) mean of each feature
sigma (ndarray): Shape (n,) standard deviation of each feature
"""
# find the mean of each column/feature
mu = np.mean(X, axis=0) # mu will have shape (n,)
# find the standard deviation of each column/feature
sigma = np.std(X, axis=0) # sigma will have shape (n,)
# element-wise, subtract mu for that column from each example, divide by std for that column
X_norm = (X - mu) / sigma
return (X_norm, mu, sigma)
#check our work
#from sklearn.preprocessing import scale
#scale(X_orig, axis=0, with_mean=True, with_std=True, copy=True)让我们看看 Z 分数标准化所涉及的步骤。
mu = np.mean(X_train,axis=0)
sigma = np.std(X_train,axis=0)
X_mean = (X_train - mu)
X_norm = (X_train - mu)/sigma
fig,ax=plt.subplots(1, 3, figsize=(12, 3))
ax[0].scatter(X_train[:,0], X_train[:,3])
ax[0].set_xlabel(X_features[0]); ax[0].set_ylabel(X_features[3]);
ax[0].set_title("unnormalized")
ax[0].axis('equal')
ax[1].scatter(X_mean[:,0], X_mean[:,3])
ax[1].set_xlabel(X_features[0]); ax[0].set_ylabel(X_features[3]);
ax[1].set_title(r"X - $\mu$")
ax[1].axis('equal')
ax[2].scatter(X_norm[:,0], X_norm[:,3])
ax[2].set_xlabel(X_features[0]); ax[0].set_ylabel(X_features[3]);
ax[2].set_title(r"Z-score normalized")
ax[2].axis('equal')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
fig.suptitle("distribution of features before, during, after normalization")
plt.show()输出:

上图显示了两个训练集参数之间的关系,"age" and "sqft"。这些都是等比例绘制的。
左: 非标准化: “ size (sqft)”特征的值范围或方差比年龄范围大得多
中间: 第一步查找删除每个特性的平均值或平均值。这样就剩下了以零为中心的特性。很难看出“ age”特性之间的差异,但“ size (sqft)”显然在零附近。
右: 第二步除以方差,这样两个特征的中心位置都为零,尺度相似。
让我们对数据进行标准化,并将其与原始数据进行比较。
# normalize the original features
X_norm, X_mu, X_sigma = zscore_normalize_features(X_train)
print(f"X_mu = {X_mu}, \nX_sigma = {X_sigma}")
print(f"Peak to Peak range by column in Raw X:{np.ptp(X_train,axis=0)}")
print(f"Peak to Peak range by column in Normalized X:{np.ptp(X_norm,axis=0)}")输出:
X_mu = [1.42e+03 2.72e+00 1.38e+00 3.84e+01], X_sigma = [411.62 0.65 0.49 25.78] Peak to Peak range by column in Raw X:[2.41e+03 4.00e+00 1.00e+00 9.50e+01] Peak to Peak range by column in Normalized X:[5.85 6.14 2.06 3.69]
通过归一化,每个列的峰值到峰值范围从几千减少到2-3。
fig,ax=plt.subplots(1, 4, figsize=(12, 3))
for i in range(len(ax)):
norm_plot(ax[i],X_train[:,i],)
ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("count");
fig.suptitle("distribution of features before normalization")
plt.show()
fig,ax=plt.subplots(1,4,figsize=(12,3))
for i in range(len(ax)):
norm_plot(ax[i],X_norm[:,i],)
ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("count");
fig.suptitle(f"distribution of features after normalization")
plt.show()输出:
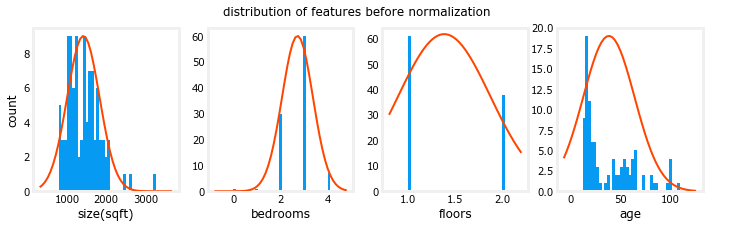

注意,在上面,规范化数据的范围以零为中心,大致为 +/-1。最重要的是,每个特性的范围是相似的。
让我们用归一化的数据重新运行我们的梯度下降法算法。注意 alpha 的大得多的值。这将加速下降。
w_norm, b_norm, hist = run_gradient_descent(X_norm, y_train, 1000, 1.0e-1, )输出:
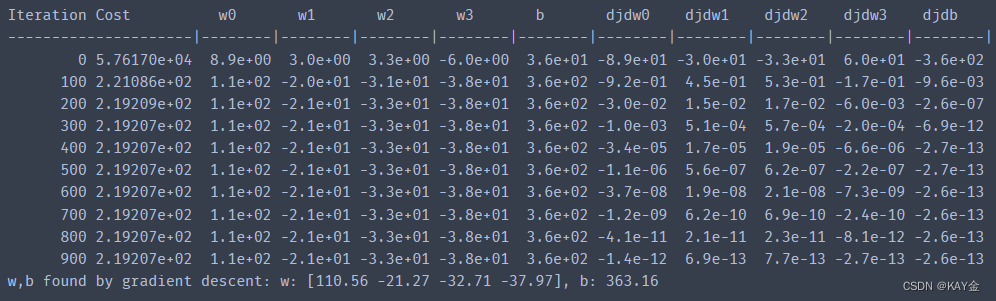
缩放功能获得非常准确的结果,快得多!.请注意,在这个相当短的运行结束时,每个参数的渐变都很小。对于具有归一化特征的回归来说,0.1的学习率是一个良好的开端。让我们把我们的预测和目标值对比一下。注意,预测是使用归一化特征,而图显示使用原始特征值。
#predict target using normalized features
m = X_norm.shape[0]
yp = np.zeros(m)
for i in range(m):
yp[i] = np.dot(X_norm[i], w_norm) + b_norm
# plot predictions and targets versus original features
fig,ax=plt.subplots(1,4,figsize=(12, 3),sharey=True)
for i in range(len(ax)):
ax[i].scatter(X_train[:,i],y_train, label = 'target')
ax[i].set_xlabel(X_features[i])
ax[i].scatter(X_train[:,i],yp,color=dlorange, label = 'predict')
ax[0].set_ylabel("Price"); ax[0].legend();
fig.suptitle("target versus prediction using z-score normalized model")
plt.show()输出:
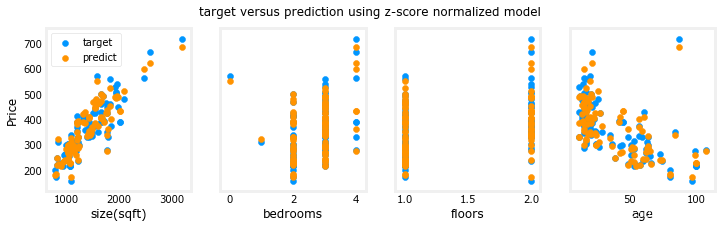
结果看起来不错,需要注意以下几点:
- 有了多个特征,我们不能再有一个单一的plot显示结果与特征。
- 在生成图形时,使用归一化特征。任何使用从规范化训练集中学到的参数的预测也必须进行规范化。
预测生成我们的模型的要点是使用它来预测数据集中没有的房价。让我们来预测一套1200平方英尺、3间卧室、1层楼、40年历史的房子的价格。回想一下,你必须用训练数据标准化时得到的平均值和标准差来标准化数据。
# First, normalize out example.
x_house = np.array([1200, 3, 1, 40])
x_house_norm = (x_house - X_mu) / X_sigma
print(x_house_norm)
x_house_predict = np.dot(x_house_norm, w_norm) + b_norm
print(f" predicted price of a house with 1200 sqft, 3 bedrooms, 1 floor, 40 years old = ${x_house_predict*1000:0.0f}")输出:
[-0.53 0.43 -0.79 0.06] predicted price of a house with 1200 sqft, 3 bedrooms, 1 floor, 40 years old = $318709
成本轮廓
查看特性扩展的另一种方法是根据成本轮廓。当特征尺度不匹配时,等高线图中的成本与参数的关系图是不对称的。
在下面的图中,参数的比例尺是匹配的。左边的图是 w [0]的成本等高线图,平方英尺与 w [1]的比值,以及标准化特征之前的卧室数量。曲线是如此的不对称,完成等高线的曲线是不可见的。相比之下,当特征标准化时,成本轮廓更加对称。其结果是,在梯度下降法期间对参数的更新可以使每个参数取得相同的进展。
plt_equal_scale(X_train, X_norm, y_train) 输出: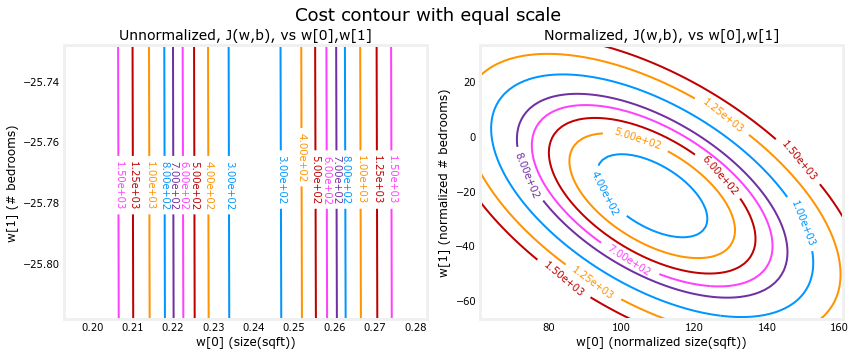
3 总结
在这个实验室里:
- 利用你在以前的实验室中开发的具有多种功能的线性回归程序
- 探讨了学习速率 α 的影响
- 利用 z 分数归一化发现了特征尺度在加速收敛中的价值