原题链接:
PTA | 程序设计类实验辅助教学平台
题面:
副本是游戏里的一个特色玩法,主要为玩家带来装备、道具、游戏资源的产出,满足玩家的游戏进程。
在 MMORPG《最终幻想14》里,有一个攻略人数最大达到 48 人的副本“零式贡希尔德神庙”,其中守关 BOSS “天佑女王”有一个很有趣的技能:“女王的大敕令”。
技能在一个 5×5 的棋盘上展开。每位玩家根据给定的两个步长,从某个方格出发,在棋盘上先走 D1 步,再走 D2 步。其中“步长”指的是曼哈顿距离,即:设两个方格的坐标分别为 (Xi,Yi) 以及 (Xj,Yj),则这两个方格的曼哈顿距离 D=∣Xi−Xj∣+∣Yi−Yj∣。
例如下图中的 A 点与 B 点的曼哈顿距离为 5:
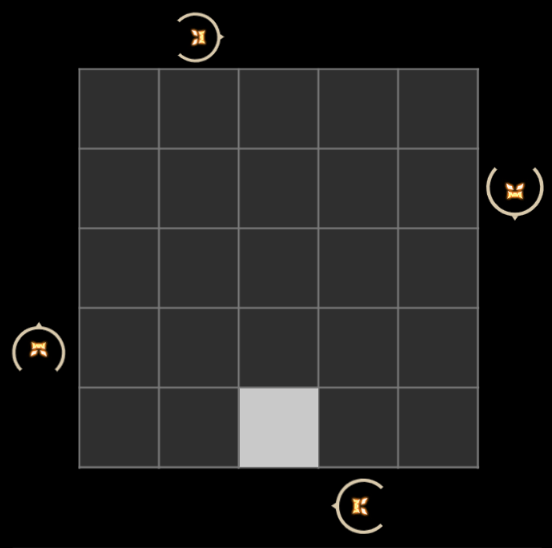
技能开始时,场地外围会出现 4 只小怪,东南西北(即棋盘的右、下、左、上)方向各出现一只小怪,且小怪一定出现在某行或某列对应的位置上。第 i 只小怪会顺时针朝固定方向移动 ni 步(题目保证不会移出界,即移动后仍然在对应着某行/某列的位置上),且:
- 北边的小怪固定向右移动;
- 东边的小怪固定向下移动;
- 南边的小怪固定向左移动;
- 西边的小怪固定向上移动。
小怪出现后,棋盘上还会出现一个发光的格子,这是玩家移动的目标点,如图所示:
玩家必须在不被小怪杀死的前提下,按规定步长,用两个回合到达目标点。技能流程如下:
1、玩家先选择一个起始方格;
2、东、西两侧的小怪开始按照固定方向移动,移动完毕后 4 只小怪会同时开展攻击,其中东、西两侧的小怪攻击自己所对应的一整行,南、北两侧的小怪攻击自己所对应的一整列。玩家若处在攻击区内则任务失败。
3、玩家移动 D1 步,到达某个方格;
4、南、北两侧的小怪开始按照固定方向移动,移动完毕后 4 只小怪会同时开展攻击,同第 2 步;
5、玩家移动 D2 步,此时必须到达目标点,否则任务失败。
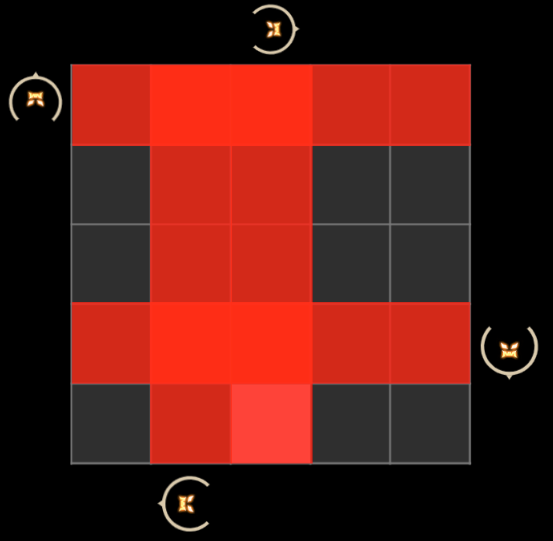
以下是上面的 4 只小怪都移动后的攻击范围的示意图:
给定小怪起始位置以及移动步数 ni 和目标点位置,请输出所有安全的移动方案,包括起始点以及第一次移动的目的地。
输入格式:
输入第一行是四个数 C1,C2,R1,R2,分别表示:
- 北边(上面)的小怪 1 在第 C1 列的位置上;
- 南边(下面)的小怪 2 在第 C2 列的位置上;
- 西边(左边)的小怪 3 在第 R1 行的位置上;
- 东边(右边)的小怪 4 在第 R2 行的位置上。
输入第二行是四个数 ni(i=1,⋯,4),按照上面的顺序给出小怪移动的步数,保证小怪移动后仍然处于某行或某列对应的位置上。
输入第三行是四个数 row,col,D1,D2,依次表示目标点的位置,以及玩家要走的两个步长。这里某方格的“位置” (row,col) 指的是该方格的行号、列号组成的二元组。
我们假设左上角的方格位置为 (1, 1)。
输出格式:
输出安全移动的方案,方案由两个位置共四个数组成,前两个数为初始选择的方格的位置,后两个数为第一次停留的位置。
对于多个方案的情况,先按初始方格位置从小到大输出,初始方格相同时按第一次停留位置从小到大输出。一个坐标 (ri,ci) 比另一个坐标 (rj,cj) 小,当且仅当 ri<rj,或 ri=rj 的同时有 ci<cj。
输入样例:
2 4 4 2 1 2 3 2 5 3 3 4输出样例:
2 1 2 4 2 3 3 1 2 3 3 5
解题思路:
先预处理出怪物两次攻击分别影响到的行和列。然后枚举合适的方案。
先枚举玩家的初始位置,在此基础上枚举玩家第一次移动的目标位置。
位置的限制条件:
1、不可在敌人当前攻击轮次的攻击范围内。
2、当前位置可达、并且可从当前位置抵达终点。比较特殊的是初始位置的判断,初始位置到终点的曼哈顿距离如果和d1+d2的差值是2的倍数,那么我们是存在可能从这个位置先走d1步再走d2步到达终点位置的,否则这个位置不可行。
具体实现细节见代码。
代码(CPP):
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e3 + 10;
const int INF = 0x3fffffff;
const int mod = 1000000007;
int C1; // 北(上)
int C2; // 南(下)
int R1; // 西(左)
int R2; // 东(右)
int n1, n2, n3, n4; // 怪物移动步数
int row, col, d1, d2; // 目标点的位置,玩家要走的两个步长
int fc1, fc2, fr1, fr2; // 第一次攻击后
int sc1, sc2, sr1, sr2; // 第二次攻击后
void initAttack() {
int c1, c2, r1, r2;
c1 = C1, c2 = C2, r1 = R1, r2 = R2;
// 第一轮
r1 -= n3;
r2 += n4;
fc1 = c1;
fc2 = c2;
fr1 = r1;
fr2 = r2;
// 第二轮
c1 += n1;
c2 -= n2;
sc1 = c1;
sc2 = c2;
sr1 = r1;
sr2 = r2;
}
void solve() {
cin >> C1 >> C2 >> R1 >> R2;
cin >> n1 >> n2 >> n3 >> n4;
cin >> row >> col >> d1 >> d2;
// 预处理两次攻击分别的覆盖行列范围
initAttack();
// 枚举判断合适的方案
for (int r = 1; r <= 5; r++) { // 枚举初始站位
if (r == fr1 || r == fr2) // 该行在第一轮攻击范围
continue;
for (int c = 1; c <= 5; c++) {
if (c == fc1 || c == fc2) // 该列在第一轮攻击范围
continue;
if (((abs(r - row) + abs(c - col)) - (d1 + d2)) % 2 != 0) // 该初始点走d1+d2步无法到达终点
continue;
// 枚举到可能适合的初始站位了, 判断这个初始站位是否可以到达终点
for (int rr = 1; rr <= 5; rr++) { // 枚举第一次行走的方格
if (rr == sr1 || rr == sr2) // 该行在第二轮攻击范围
continue;
for (int cc = 1; cc <= 5; cc++) {
if (cc == sc1 || cc == sc2) // 该列在第二轮攻击范围
continue;
if ((abs(rr - r) + abs(cc - c)) != d1) // 这个位置不可以从初始位置到达
continue;
if ((abs(rr - row) + abs(cc - col)) != d2) // 这个位置不可以抵达终点
continue;
// 找到了适合的方案,输出
cout << r << " " << c << " " << rr << " " << cc << endl;
}
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(18);
solve();
return 0;
}