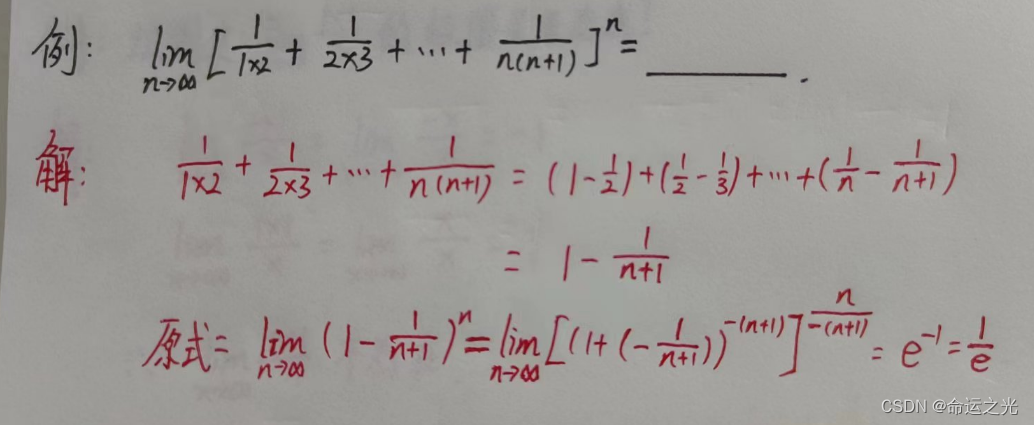【微信小程序-uniapp】CustomDialog 居中弹窗组件
news2026/2/9 0:01:28
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/754572.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
nginx的前端集成
对于springcloud项目,后端我们有很多的微服务,当然前端我们也可以有很多的小项目进行集成
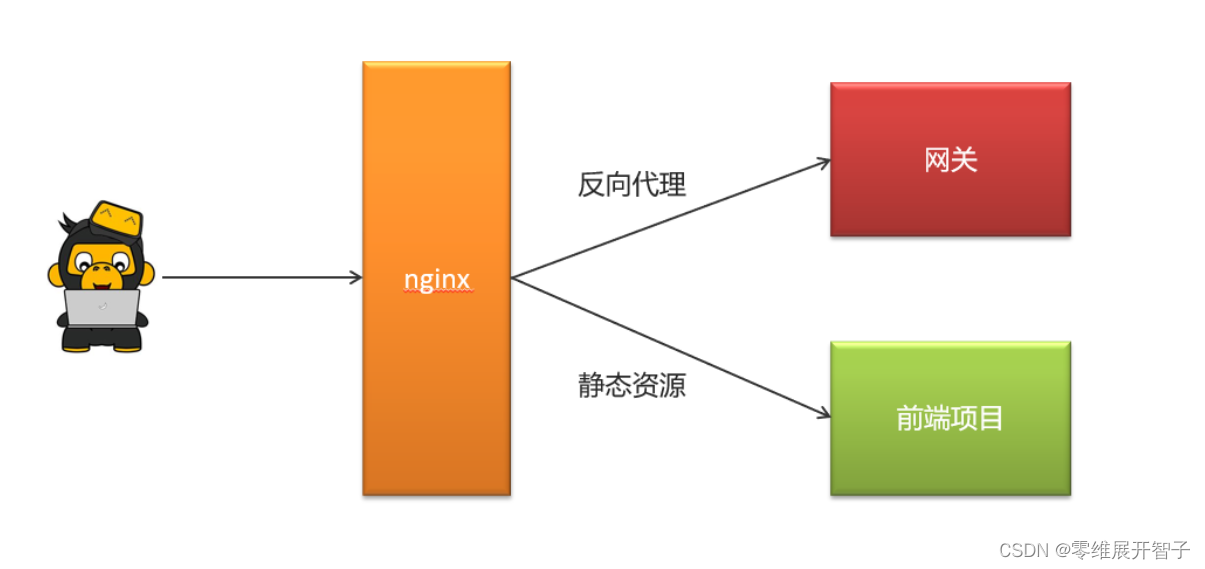
前端项目部署思路 通过nginx来进行配置,功能如下 通过nginx的反向代理功能访问后台的网关资源 通过nginx的静态服务器功能访问前端静态页面 配置ng…
错过直播?快收藏详实回顾!Get「研发效能管理」7 步实践指南与案例剖析
目录
效能提升,无论企业规模大小,研发效能管理不可或缺
头部大厂
腰部厂商
中小型企业
研发效能管理 GDAI 模型,监管与迭代相辅相成,效能螺旋上升
研发效能管理 7 步走,明晰 6 大角色场景,有的放矢&a…
自动化测试面临的问题剖析
前面的文章为大家介绍了我们内部在使用的一些自动化框架,大家可以了解到我们使用的自动化测试框架太多。测试工程师就会面临这样的问题:到底应该选择哪个框架?应该选择哪种脚本语言?有什么办法能降低编写脚本的门槛?这…
攻防世界-Crypto-easy_ECC
题目描述:一道数学题
已知椭圆曲线加密Ep(a,b)参数为
p 15424654874903
a 16546484
b 4548674875
G(6478678675,5636379357093)
私钥为
k 546768
求公钥K(x,y)
1. 思路分析
这个没啥好说的,就是一道数学题,关键在于ECC算法的原…
安装部署rancher2.7.0,然后导入K8S集群,管理集群
1. 安装rancher2.7.0
docker run -d --name rancher --restartunless-stopped --privileged -p 80:80 -p 443:443 -v /var/lib/rancher:/var/lib/rancher/ -v /var/log/rancher/auditlog:/var/log/auditlog rancher/rancher:v2.7.02.浏览器登录
2.1 利用默认账号登…
中电金信:技术实践|异构数据库迁移之“痛”
导语:
近几年,国产化创新潮流席卷全国,异构数据库迁移成了不少同行、客户争相讨论的话题,大家或争论方案、或求解答疑、或讨论产品,总之问题林林总总,涉及的面还很多,笔者也在近期的几个项目中…
Java正则表达式简介及Jar包
Java提供了java.util.regex包,用于与正则表达式进行模式匹配。 Java正则表达式与Perl编程语言非常相似,非常容易学习。
正则表达式定义了字符串的模式。
正则表达式可以用来搜索、编辑或处理文本。
正则表达式并不仅限于某一种语言,但是在…
低代码技术:提高效率降低成本的全新选择
一、前言 企业想要独立的应用程序,开发者在寻求更快速、更高效、更灵活的开发方法,以适应快速变化的市场需求。在这个背景下,低代码技术以提高效率降低成本的方式走进人们视野,成为了一种全新的应用程序开发方式。 二、相比传统的…
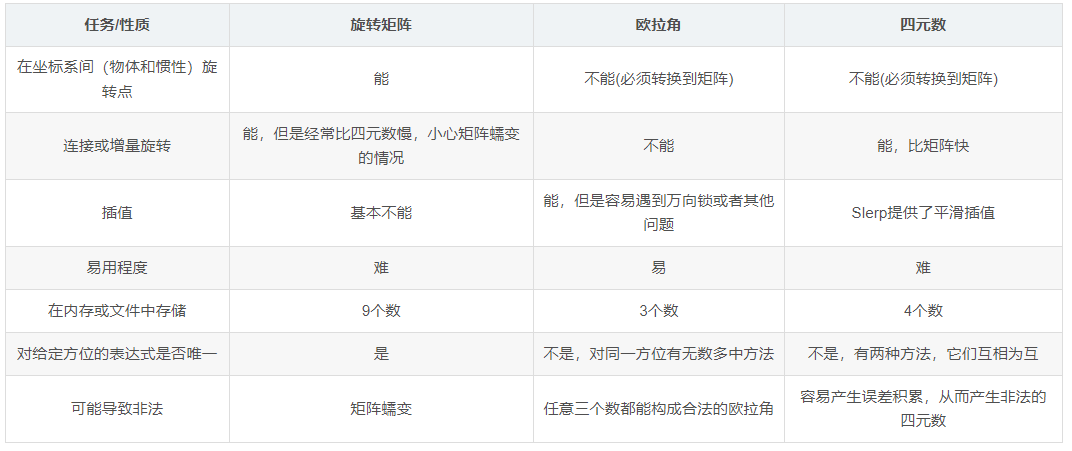
刚体三维运动学【旋转矩阵】【欧拉角】【四元素】
一些概念
轴角法、旋转矩阵、欧拉角、四元数主要用于:向量的旋转、坐标系之间的转换、角位移的计算、方位的平滑插值计算。坐标系的旋转一共有三种表示方法:旋转矩阵、欧拉角和四元数。一般指地面系(世界系)和机体系之间的旋转关…
UE4.27 编译及打包HTML5相关资料
UE4.27 编译及打包HTML5相关资料
UE官方资料 https://docs.unrealengine.com/4.27/zh-CN/SharingAndReleasing/HTML5/GettingStarted/ B站视频资料 UE4.27可以打包HTML5啦 Github 中文文档
https://github.com/Xi3Chen/UE4.27PackingH5DDoc emsdk 交叉编译环境安装 Emscripte…
零售数字化转型如何破局?这篇文章全说清了!
“数字化转型”,一个老生常谈的话题。自19世纪互联网崭露头角,亚马逊和eBay等电商平台崛起,引领电子商务的发展。传统零售业开始意识到在线渠道的重要性,并纷纷推出自己的电子商务网站,从自此进入数字化转型的赛道当中…
【UniApp开发小程序】请求包创建+登录功能实现
文章目录 请求包创建创建文件夹请求工具request.js 登录功能实现请求方法页面涉及知识点错误提示前端校验设置token到客户端缓存中路由跳转 请求包创建
小程序的数据需要向后端发请求进行获取,为了简化后续的开发,需要创建一个包专门存放所有发请求的js…
Kong 自定义插件安装和调试
文件格式
官方文档
├── kong-plugin-mepjwt-0.1.0-1.all.rock # luarocks安装依赖 luarocks pack生成的文件
├── kong-plugin-mepjwt-0.1.0-1.rockspec # luarocks的安装依赖
└── mepjwt├── handler.lua # 主要处理业务逻辑的文件├── jwt_parser.lua # 依…
Android Framework岗位面试真题分享
Handler是Android中的消息处理机制,是一种线程间通信的解决方案,同时你也可以理解为它天然的为我们在主线程创建一个队列,队列中的消息顺序就是我们设置的延迟的时间,如果你想在Android中实现一个队列的功能,不妨第一时…
【量化课程】02_1.宏观经济学基础概念
2.1_宏观经济学基础概念 文章目录 2.1_宏观经济学基础概念1. 宏观经济简单背景1.1 微观经济学时期1.2 宏观经济学开端1.3 宏观经济学研究的问题1.4 宏观经济与理财的联系 2. 宏观经济分析及关键指标2.1 教材中的宏观经济分析框架和指标2.1.1 国内生产总值GDP2.1.2 边际消费倾向…
vcruntime140.dll重新安装方法,vcruntime140.dll修复教程
vcruntime140.dll是Microsoft Visual C Redistributable的一部分,它是Windows操作系统上非常重要的一个动态链接库文件。这个文件包含了一些运行时库函数,用于支持运行在Windows上使用了Microsoft Visual C开发的软件。如果电脑系统中缺失vcruntime140.d…
【Unity面试篇】Unity 面试题总结甄选 |Unity性能优化 | ❤️持续更新❤️
前言
关于Unity面试题相关的所有知识点:🐱🏍2023年Unity面试题大全,共十万字面试题总结【收藏一篇足够面试,持续更新】为了方便大家可以重点复习某个模块,所以将各方面的知识点进行了拆分并更新整理了新…
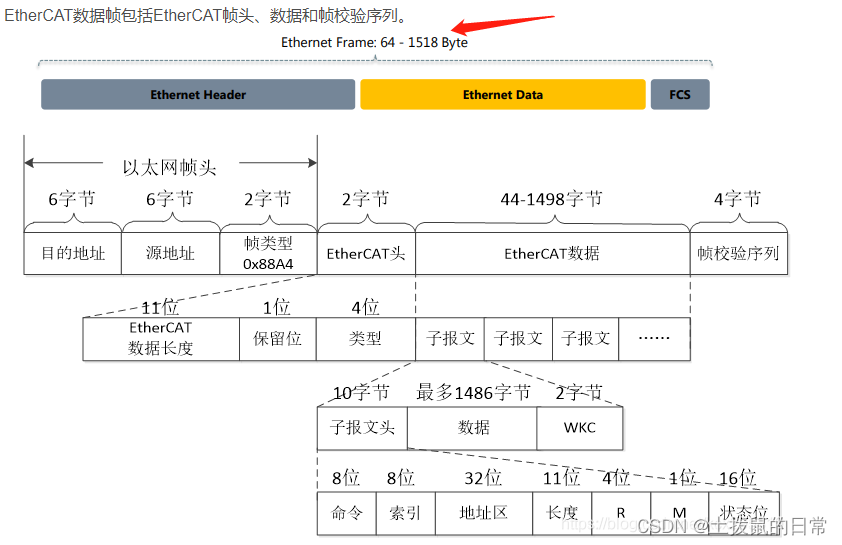
SOEM_1(笔记,从别的博客文章学的笔记)
目录介绍:
doc:帮助文档、 osal:主要是用于符合OSADL和实时进程创建。也就是说:发送EtherCAT数据包不能抖动太大,如果直接使用linux提供的原生线程,可能实时性无法满足。需要对Linux内核打上实时补丁&…
高等数学❤️第一章~第二节~极限❤️极限的概念与性质~数列极限详解
【精讲】高等数学中的数列极限解析 博主:命运之光的主页 专栏:高等数学 目录
导言
一、数列极限的定义
二、数列极限的判定方法
三、数列极限的性质
必需记忆知识点 例题(用于熟悉数列极限)
例题1
例题2
例题3
结论 导言…
【QQ好友列表展示-设置HeaderView Objective-C语言】
一、好,看一下,刚才我们这个btnGroupTitle的frame为什么是0 现在我们首先知道,当你程序一运行起来以后,你这里的self,就是 当你程序运行起来以后,这个headerView 的frame,默认应该是0的
就是我们看到的效果,它应该都是0 的
一开始都是0 的
那么其实也就是说,是这样…