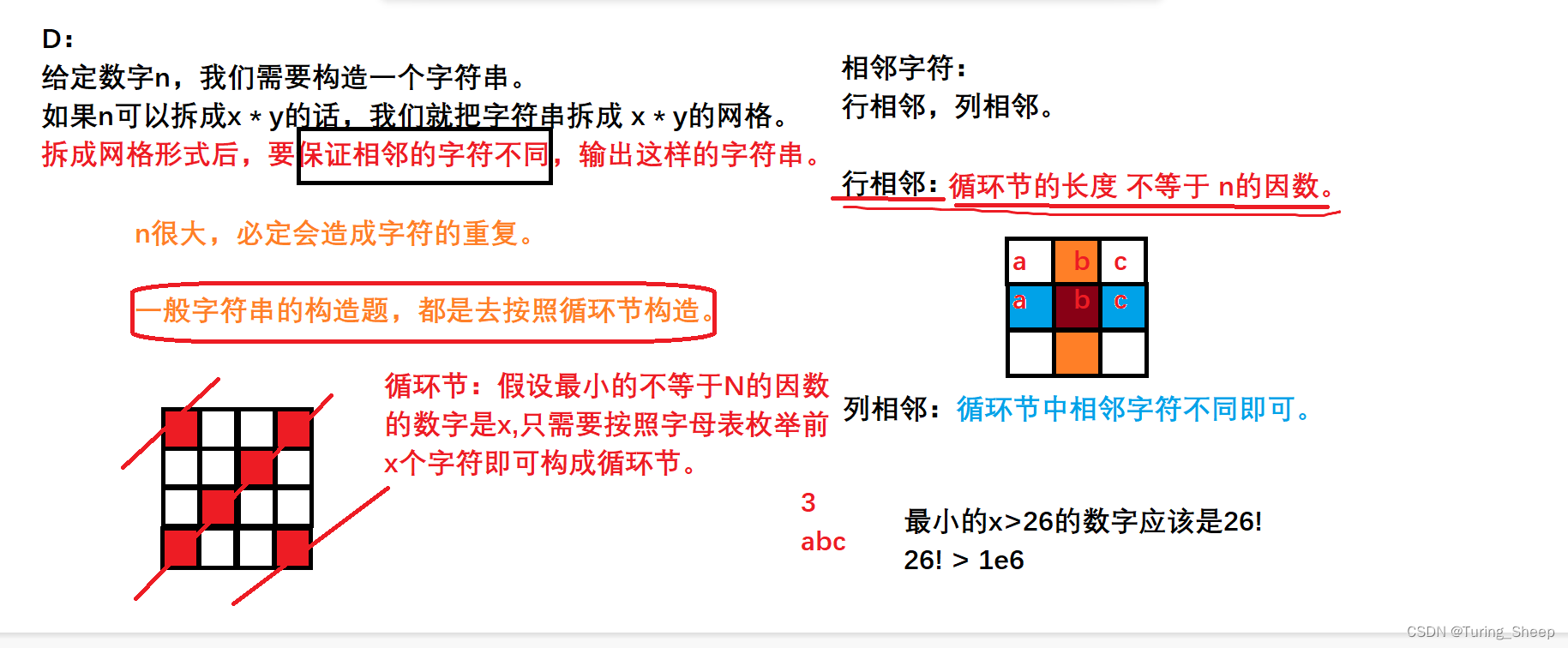
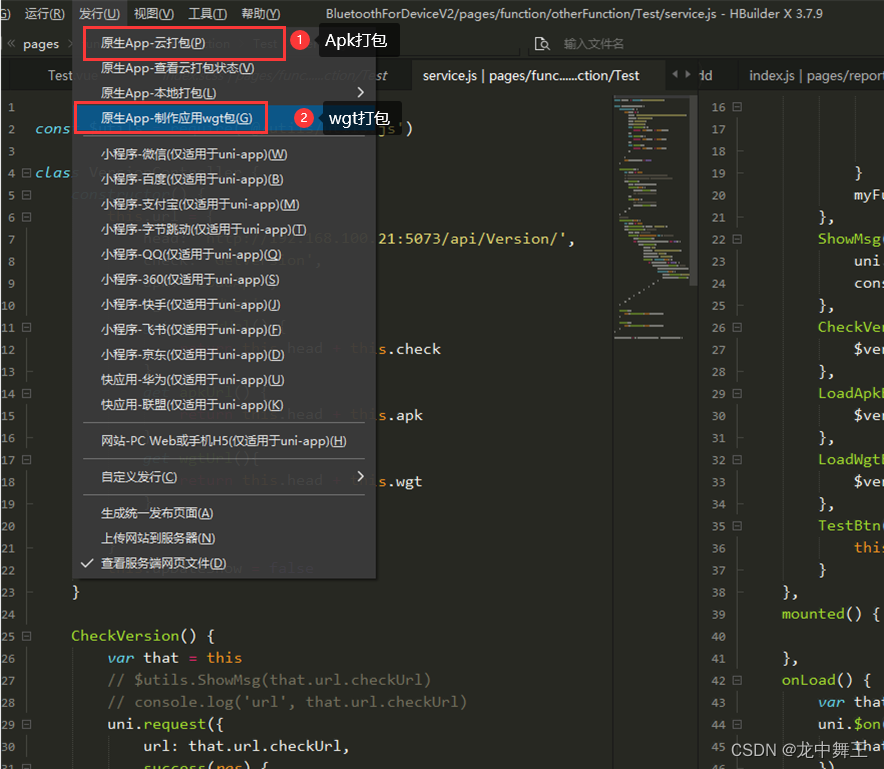
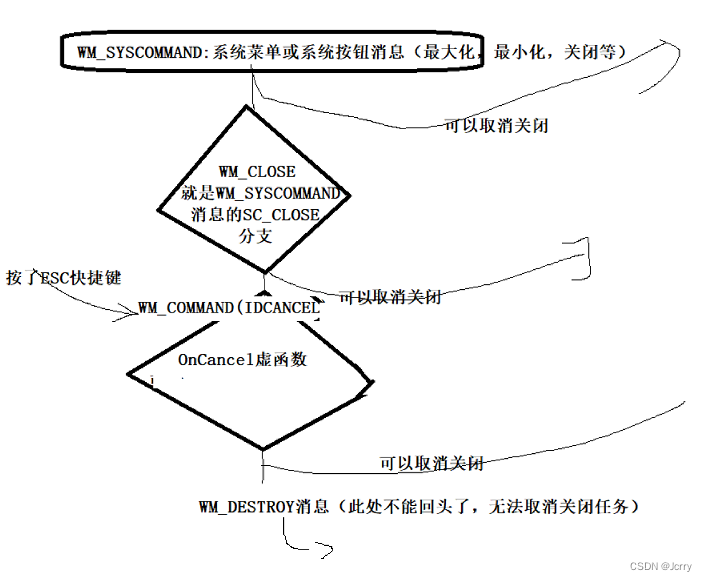
一些概念
- 轴角法、旋转矩阵、欧拉角、四元数主要用于:向量的旋转、坐标系之间的转换、角位移的计算、方位的平滑插值计算。
- 坐标系的旋转一共有三种表示方法:旋转矩阵、欧拉角和四元数。
- 一般指地面系(世界系)和机体系之间的旋转关系。
- 已知点p在机体系的坐标,求在地面系的坐标。
- 为什么要进行坐标转换??一个公式的所有物理量要表示在同一个坐标系内。
- 欧拉角 、四元素和旋转矩阵这些表示方式都是为 表示一种旋转过程。从姿态A转到姿态B,使用旋转T,则T可用这些方式表示。
对比
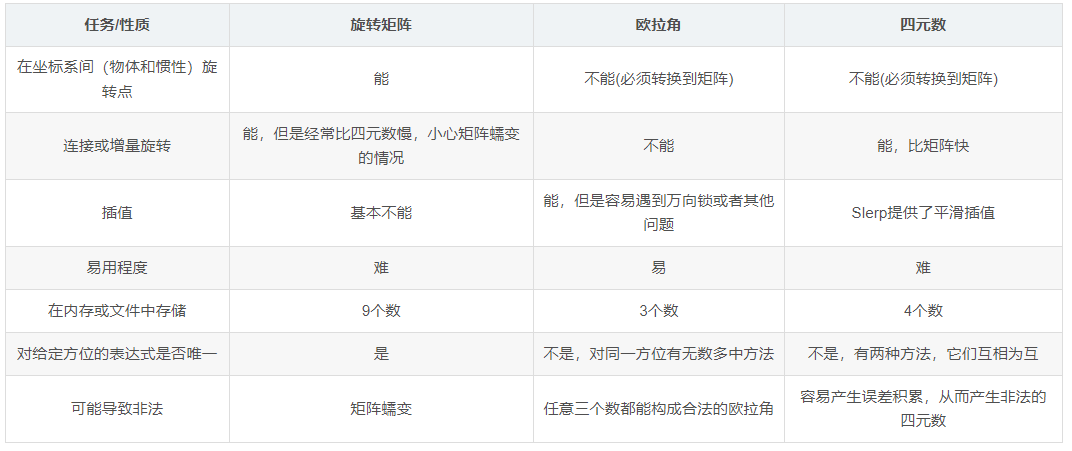
旋转矩阵,欧拉角,四元数主要用于:向量的旋转、坐标系之间的转换、角位移的计算、方位的平滑插值计算。
不同的方位表示方法适用于不同的情况:
- 欧拉角最容易使用。当需要为世界中的物体指定方位时,欧拉角能大大简化人机交互,包括直接键盘输入方位、在代码中指定方位(如为渲染设定摄像机)、在调试中测试。
- 如果需要在坐标系之间转换向量,就选择矩阵形式。另一种方法是用欧拉角作为方位的“主拷贝“,但同时维护一个旋转矩阵,当欧拉角发生改变时,矩阵也要同时进行更新。
- 当需要大量保存方位数据(如动画)时,就使用欧拉角或者四元数,欧拉角少占用25%内存,但是转换到矩阵慢。如果动画数据需要嵌套坐标系之间的连接,四元数可能是最好的选择。
- 平滑插值只能用四元数。用其它形式则必须转到四元数,插值完毕再转回去。
轴角法
描述两个坐标系之间的旋转关系;
用一次旋转表示两坐标系的旋转关系;
原理概述
在三维空间中。一个xyz坐标系绕某一个定轴旋转某一个角度就得到了新的坐标系x’y’z’。那反过来说,一个xyz坐标系和另一个x’y’‘z’,是否可以找到一个轴和一角,旋转一次就可以使两个坐标系重合呢?答案是肯定的,那就是轴角法!
轴角法用一个以单位矢量定义的旋转轴,再加上一个标量定义的旋转角来表示旋转。通常的表示[x,y,z,theta],前面三个表示轴,最后一个表示角度。表示非常直观,也很紧凑。
优缺点
优点一:同轴的两次旋转可以直接相加来等效为一次旋转。
优点二:定义简单,相对直观。
硬伤一:当旋转角度是0的时候,旋转轴可以是任意的,即当旋转角是0时旋转关系不唯一。
硬伤二:两次连续的旋转怎样合成呢?或者说是两个旋转如何做差呢?答案是没办法,除非借助其他表示方法。
事实上,有人已经证明了,虽然旋转的自由度是三,但是仅仅用三个数表示必然会出问题。
那需要几个呢?最少四个数,即四元素。
四元数和轴角法什么关系呢?是如何解决轴角法两大硬伤的呢??
参考:https://zhuanlan.zhihu.com/p/94584704
四元素
描述两个坐标系之间的旋转关系;
用一次旋转表示两坐标系的旋转关系;
四元数和轴角法的关系?因此可以把四元数认为是轴角法的一个数学工具. 它解决了轴角法两个致命的缺点!
解决了轴角法、旋转矩阵发中,旋转关系不唯一(死锁?万向锁?)的致命问题!
旋转矩阵
描述两个坐标系之间的旋转关系;
经过三次旋转;
用途
- 两坐标之间的旋转关系(坐标转换);
- 点p绕某轴旋转了某个角度,求旋转后的坐标(向量旋转);
- 方位的平滑插值计算;
坐标系的旋转问题
点绕坐轴系旋转后的坐标求解问题
欧拉角
旋转遵循右手定则;
旋转方式不同领域有不同的规范,不同之处在于以下两点:
(1)绕定轴还是动轴;
(2)xyz轴先绕哪个轴再绕哪个轴?
在航天航空领域,欧拉角的定义为:
将坐标系旋转关系分解为3个方向上的转动;
按照Z–>Y–>X的顺序转动;
步骤:
一开始,地面系oxyz与机体系o’x’y’z’重合;
机体系先绕z轴旋转得到偏航角yaw;
再绕旋转后的y’轴旋转得到俯仰角pitch;
最后绕旋转后的x’轴旋转得到横滚角roll;
参考:https://zhuanlan.zhihu.com/p/98320567