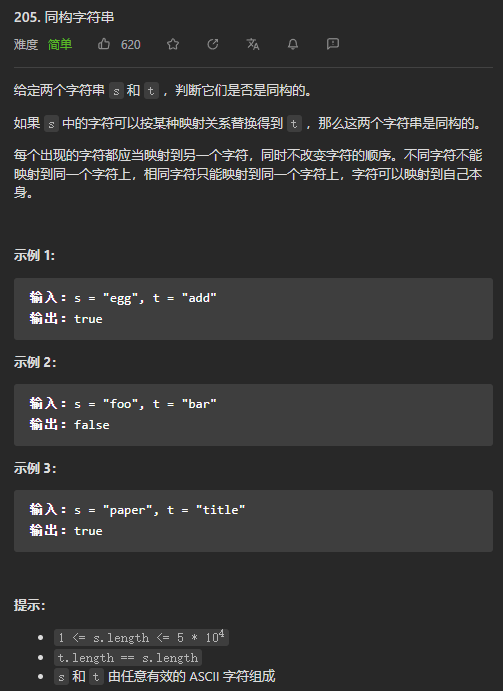
需要判断s和t每个位置上的字符是否都一一对应，即s的任意一个字符被t中唯一的字符对应，同时t的任意一个字符被s中唯一的字符对应。这也被称为【双射】的关系。

以示例二为例，t中的字符a和r虽然有唯一的映射o，但对于s中的字符o来说，其存在两个映射{a,r}，故不满足条件。

因此，维护两张哈希表，第一张哈希表s2t以s中字符为键，映射至t的字符为值，第二张哈希表t2s以t中字符为键，映射至s的字符为值。从左至右遍历两个字符串的字符，不断更新两张哈希表，如果出现冲突（即当前下标index对应的字符s[index]已经存在映射且不为t[index]或当前下标index对应的字符t[index]已经存在映射且不为s[index]）时，说明两个字符串无法构成同构，返回false。

如果遍历结束没有出现冲突，则表明两个字符串是同构的。

import java.util.HashMap;
import java.util.Map;

class Solution {
    public boolean isIsomorphic(String s, String t) {
        Map<Character, Character> s2t = new HashMap<>();
        Map<Character, Character> t2s = new HashMap<>();
        int len = s.length();
        for (int i = 0; i < len; i++) {
            char x = s.charAt(i);
            char y = t.charAt(i);
            if ((s2t.containsKey(x) && s2t.get(x) != y) || (t2s.containsKey(y) && t2s.get(y) != x)) {
                return false;
            }
            s2t.put(x, y);
            t2s.put(y, x);
        }
        return true;
    }
}

复杂度分析：

• 时间复杂度：O(n)，其中n为字符串的长度。只需同时遍历一遍字符串s和t即可。
• 空间复杂度：O($|\sum |$)，其中$\sum$是字符串的字符集。哈希表存储字符的空间取决于字符串的字符集大小，最坏情况下每个字符均不相同，需要O(|$\sum$|)的空间。