跳表结构设计

跳表是在链表基础上改进过来的，实现了一种「多层」的有序链表，这样的好处是能快读定位数据。

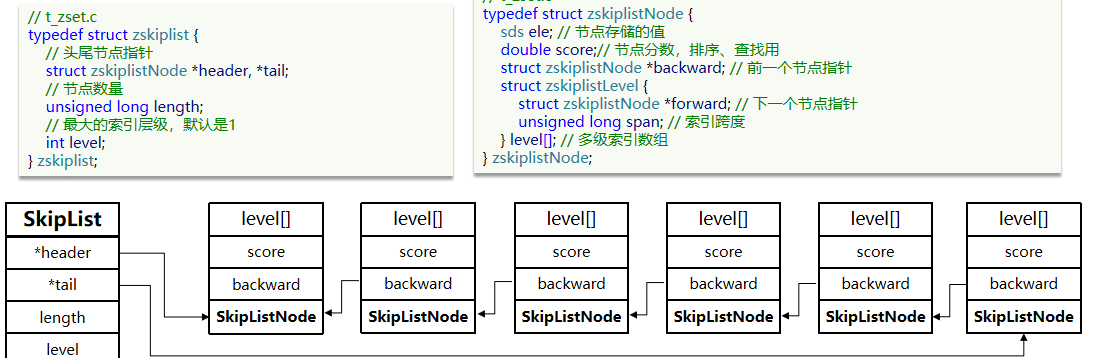
跳表结构里包含：

跳表的头尾节点，便于在O(1)时间复杂度内访问跳表的头节点和尾节点；
跳表的长度，便于在O(1)时间复杂度获取跳表节点的数量；
跳表的最大层数，便于在O(1)时间复杂度获取跳表中层高最大的那个节点的层数量；

跳表节点结构设计

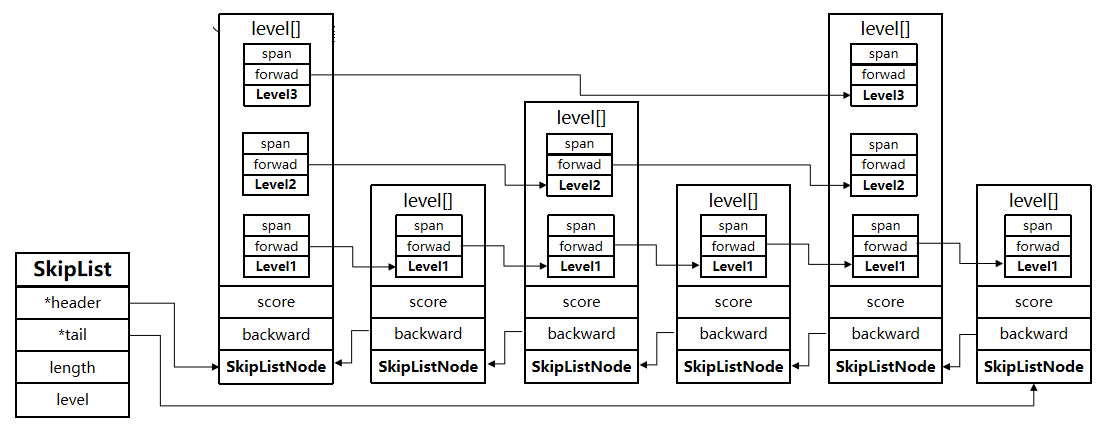
图中头节点有 L1~L3 三个头指针，分别指向了不同层级的节点，然后每个层级的节点都通过指针连接起来：

L1 层级共有 5 个节点，分别是节点1、2、3、4、5；
L2 层级共有 3 个节点，分别是节点1、3、5；
L3 层级只有 1 个节点，也就是节点1、5 。

跳表节点查询过程

查找一个跳表节点的过程时，跳表会从头节点的最高层开始，逐一遍历每一层。在遍历某一层的跳表节点时，会用跳表节点中的 SDS 类型的元素和元素的权重来进行判断，共有两个判断条件：

如果当前节点的权重「小于」要查找的权重时，跳表就会访问该层上的下一个节点。
如果当前节点的权重「等于」要查找的权重时，并且当前节点的 SDS 类型数据「小于」要查找的数据时，跳表就会访问该层上的下一个节点。
若上面两个条件都不满足，或者下一个节点为空时，跳表就会使用目前遍历到的节点的 level 数组里的下一层指针，然后沿着下一层指针继续查找，这就相当于跳到了下一层接着查找。

情景：有个 3 层级的跳表，查找【元素：abcd，权重：4】的节点，查找的过程是这样的

先从头节点的最高层开始，L2 指向了「元素：abc，权重：3」节点，这个节点的权重比要查找节点的小，所以要访问该层上的下一个节点；
但是该层的下一个节点是空节点（ leve[2]指向的是空节点），于是就会跳到「元素：abc，权重：3」节点的下一层去找，也就是 leve[1];
「元素：abc，权重：3」节点的 leve[1] 的下一个指针指向了「元素：abcde，权重：4」的节点，然后将其和要查找的节点比较。虽然「元素：abcde，权重：4」的节点的权重和要查找的权重相同，但是当前节点的 SDS 类型数据「大于」要查找的数据，所以会继续跳到「元素：abc，权重：3」节点的下一层去找，也就是 leve[0]；
「元素：abc，权重：3」节点的 leve[0] 的下一个指针指向了「元素：abcd，权重：4」的节点，该节点正是要查找的节点，查询结束。

跳表节点层数设置

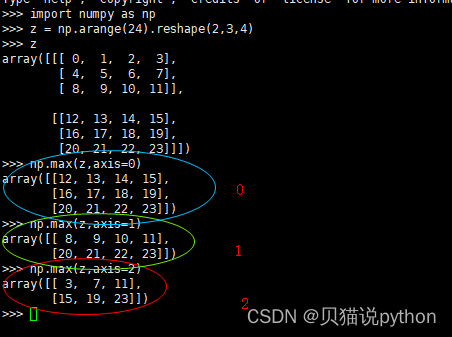
跳表的相邻两层的节点数量最理想的比例是 2:1，查找复杂度可以降低到 O(logN)

Redis实现做法是，跳表在创建节点时候，会生成范围为[0-1]的一个随机数，如果这个随机数小于 0.25（相当于概率 25%），那么层数就增加 1 层，然后继续生成下一个随机数，直到随机数的结果大于 0.25 结束，最终确定该节点的层数。

最大层数有阈值限制，ZSKIPLIST_MAXLEVEL控制，Redis 7.0 定义为 32，Redis 5.0 定义为 64，Redis 3.0 定义为 32。

创建跳表时，就会直接创建ZSKIPLIST_MAXLEVEL层高的头节点，源码如下：

/* Create a new skiplist. */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

为什么用跳表不用红黑树？

从内存占用上来比较，跳表比平衡树更灵活一些。平衡树每个节点包含 2 个指针（分别指向左右子树），而跳表每个节点包含的指针数目平均为 1/(1-p)，具体取决于参数 p 的大小。如果像 Redis里的实现一样，取 p=1/4，那么平均每个节点包含 1.33 个指针，比平衡树更有优势。
在做范围查找的时候，跳表比平衡树操作要简单。
从算法实现难度上来比较，跳表比平衡树要简单得多。平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而跳表的插入和删除只需要修改相邻节点的指针，操作简单又快速。