我的评价是毒瘤😅

首先想到的肯定是原树上的直径。

于是得到第一个结论：这条边的两个端点一定在直径上。

第二个结论：每个点距离最远的那个点是直径的两个端点之一。

发现直径上形成了一个环。显然这个环的长度应该$\ge L$，因此对于环外的点是很好讨论的。

发现环上的点比较难处理，所以想到二分来增加限制。设直径的两个端点是$u,v$，假设固定了环的右端点$i$，发现可以直接把$\text{dist(u,j)}$的范围解出来，二分即可。

写了一发，结果直接全$\text{wa}$。。。请教某位不愿透露姓名的大佬过后发现第二个结论是错的。。。并且给出了构造。。。

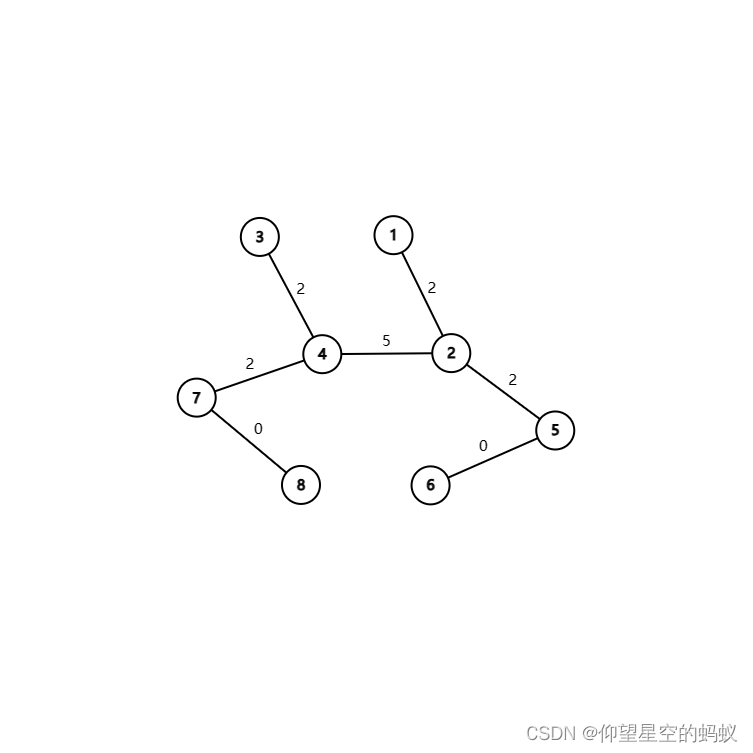
比如说这个图。。。显然直径是$8\to 6$，考虑在$5,7$之间添加一条长度为$3$的边，这样距离最远的点对是$1,3$，显然都不是直径的端点。。。

其实之前那个做法都想的差不多了，就是拆式子。。。

又要重新推一遍。。。烦死了。。。考场上肯定是打不完了。。。

考虑限制点对的时候，如果钦定$i<j$，去判断$di{s}_i+di{s}_j+dis(j,u)-dist(i,u)>mid$，那么无论怎么做都是二维数点；但是实际上可以证明二分的下界是$2\max (di{s}_i)$，这样就不用考虑$i,j$的大小关系了，可以优化掉一个$\log$。总之发现只用移动指针就做完了。

虽然对复杂度影响也不是很大。

复杂度$O(n\log n)$。

$\text{remark}$ 感觉挺难想到一来就拆式子的。。。

#include<bits/stdc++.h>
#define fi first
#define se second
#define ll long long
#define pb push_back
#define db double
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N=1e5+5;
int n,U,V,a[N],cnt,ban[N];
ll len,diam,dis[N],pre[N],dis2[N],Max[N],tmp[N];
vector<pair<int,int>>G[N];
void dfs(int u,int topf,int &rt){
    if(rt==0||dis[u]>dis[rt])rt=u;
    for(auto v:G[u]){
        if(v.fi==topf)continue;
        pre[v.fi]=u,dis[v.fi]=dis[u]+v.se,dfs(v.fi,u,rt);
    }
}
int find(ll L,ll R,int ps){
    int l=lower_bound(tmp+1,tmp+1+ps,L)-tmp;
    int r=upper_bound(tmp+1,tmp+1+ps,R)-tmp;
    if(r-l>0)return 1;
    return 0;
}
void locate(int u,int topf,ll &Max){
    Max=max(Max,dis2[u]);
    for(auto v:G[u]){
        if(v.fi==topf||ban[v.fi])continue;
        dis2[v.fi]=dis2[u]+v.se,locate(v.fi,u,Max);
    }
}
vector<pair<ll,int>>vec1,vec2;
ll s1[N],s2[N],s3[N],s4[N];
int check(ll mid){
    assert(vec1.size()==cnt);
    assert(vec2.size()==cnt);
    s1[cnt]=-inf,s2[cnt]=inf,s3[cnt]=-inf,s4[cnt]=inf;
    for(int i=cnt-1;i>=0;i--){
        int j=vec1[i].se;
        s1[i]=max(s1[i+1],-dis[j]+Max[j]);
        s2[i]=min(s2[i+1],-dis[j]-Max[j]);
        s3[i]=max(s3[i+1],dis[j]+Max[j]);
        s4[i]=min(s4[i+1],dis[j]-Max[j]);
    }
    ll A=-inf,B=inf,C=-inf,D=inf;
    int j=cnt;
    for(int i=0;i<cnt;i++){
        while(j-1>=0&&vec2[i].fi+vec1[j-1].fi>mid){
            j--;
        }
        int x=vec2[i].se;
        A=max(A,dis[x]+Max[x]+s1[j]+len-mid);
        B=min(B,dis[x]-Max[x]+s2[j]+mid-len);
        C=max(C,dis[x]+Max[x]+s3[j]+len-mid);
        D=min(D,dis[x]+dis[x]-Max[x]+s4[j]+mid-len);
    }
    swap(A,B),A=-A,B=-B;
    for(int i=2;i<=cnt;i++){
        ll L=max(C-tmp[i],-B+tmp[i]),R=min(D-tmp[i],-A+tmp[i]);
        if(find(L,R,i-1))return 1;
    }
    return 0;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
    while(cin>>n>>len&&(n||len)){
        for(int i=1;i<=n;i++)G[i].clear();
        for(int i=1;i<n;i++){
            int x,y,z;cin>>x>>y>>z;
            G[x].pb({y,z});
            G[y].pb({x,z});
        }
        U=V=0,dis[1]=0,dfs(1,0,U),dis[U]=0,dfs(U,0,V),diam=dis[V];
        int x=V;cnt=0;while(x!=U)a[++cnt]=x,x=pre[x];
        a[++cnt]=x;reverse(a+1,a+1+cnt);
        for(int i=1;i<=n;i++)ban[i]=0;
        for(int i=1;i<=cnt;i++)ban[a[i]]=1;
        for(int i=1;i<=cnt;i++)Max[a[i]]=0,dis2[a[i]]=0,locate(a[i],0,Max[a[i]]);
        for(int i=1;i<=cnt;i++)tmp[i]=dis[a[i]];
        vec1.clear(),vec2.clear();
        for(int i=1;i<=cnt;i++)vec1.pb({dis[a[i]]+Max[a[i]],a[i]});
        for(int i=1;i<=cnt;i++)vec2.pb({-dis[a[i]]+Max[a[i]],a[i]});
        sort(vec1.begin(),vec1.end()),sort(vec2.begin(),vec2.end());
        ll l=0,r=diam,res=diam;
        //fixed
        for(int i=1;i<=cnt;i++)l=max(l,2*Max[a[i]]);
        while(l<=r){
            ll mid=l+r>>1;
            if(check(mid))res=mid,r=mid-1;
            else l=mid+1;
        }
        cout<<res<<"\n";
    }
}