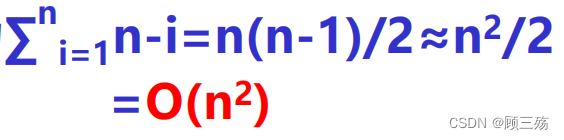目录

一、概述

（1）基本概念

（2）排序分类

（3）排序文件的物理表示 —— 数组表示

二、插入排序（通过比较插入实现排序）

（1）直接插入排序

① 过程

② 算法

③ 算法分析

④ 常用的插入排序方法

⑤ 示例

三、交换排序（通过比较交换实现排序）

（1）冒泡排序

① 基本思想

② 算法

③ 算法分析

④ 示例

（2）快速排序

① 基本思想

② 过程

③ 算法

④ 算法分析

⑤ 示例 

四、选择排序（以重复选择的思想为基础进行排序）

（1）直接选择排序

① 过程

② 算法

③ 算法分析

④ 示例

（2）堆排序

① 堆

② 建堆（筛选法） 

③ 过程

④ 算法

⑤ 算法分析

⑥ 示例

五、归并排序

（1）有序序列的合并（两个有序表归并成一个有序表）

① 思想

② 算法（两个有序表归并算法）

（2）二路归并排序

① 思想 

② 算法

③ 算法分析

④ 示例

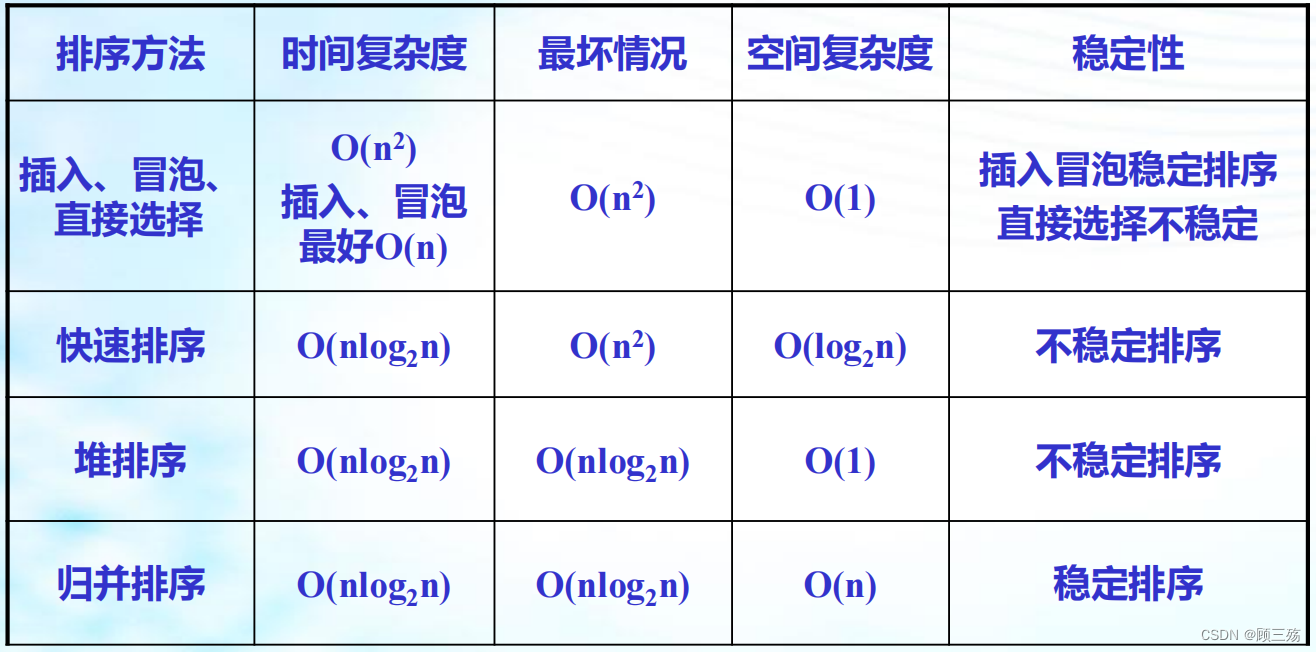
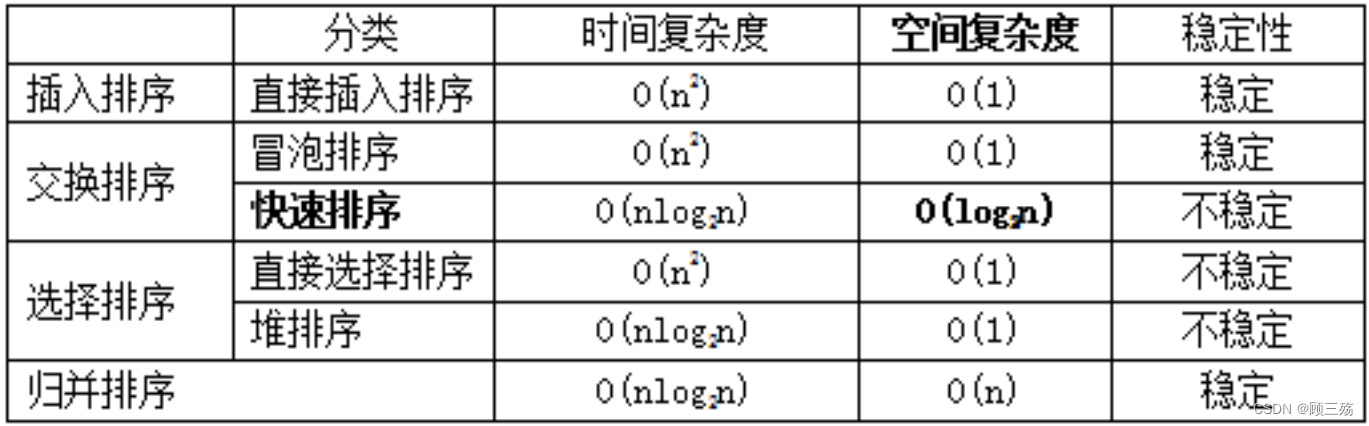
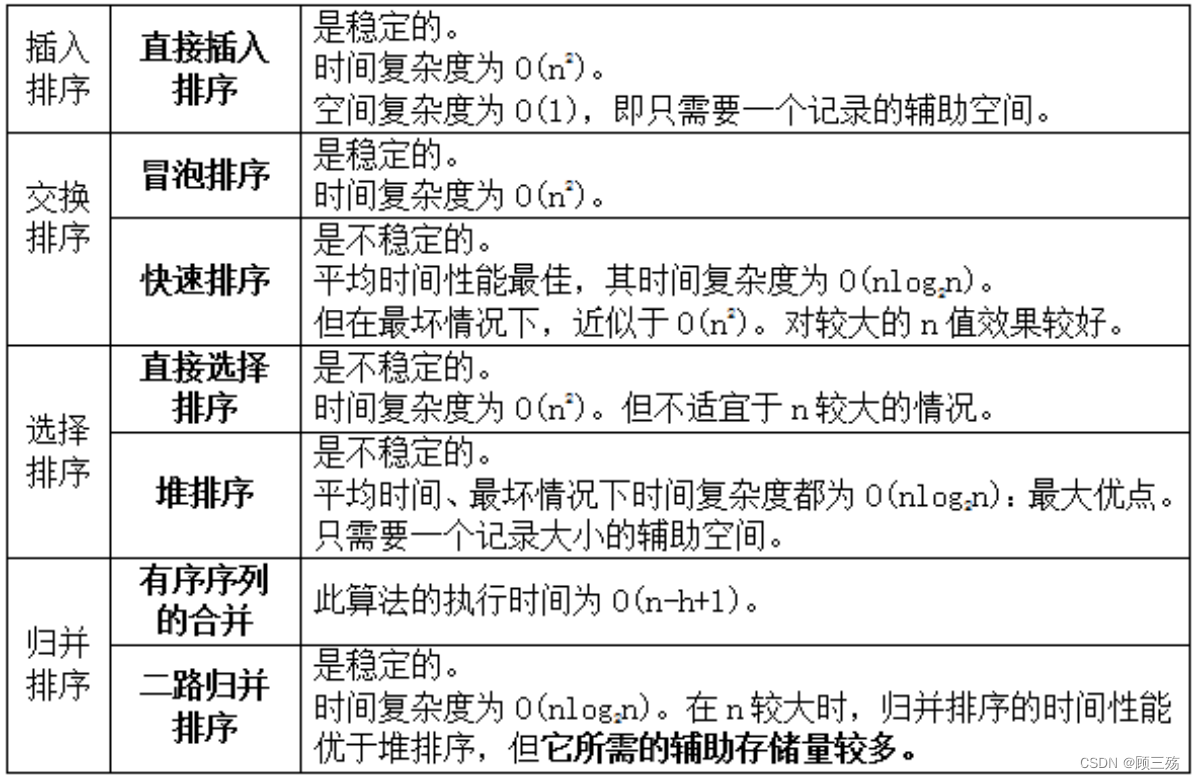
六、各种排序方法的比较 

 

---

---

一、概述

（1）基本概念

数据排序 ： 将一个文件的记录按关键字不减（ 或不增）次序排列，使文件成为有序文件，此过 程称为排序。 

稳定排序 ： 若排序后， 相同关键字的记录保持 它们原来的相对次序 ，则此排序方法称为稳定排序。 

• 稳定性是排序方法本身的特性，与数据无关
• 换句话说，一种排序方法如果是稳定的， 则对所有的数据序列都是稳定的

不稳定排序：如果在一组数据上出现不稳定的现象，则该方法是不稳定的。

排序类型：

• 内部排序：全部数据存于内存 
• 外部排序：需要对外存进行访问的排序过程

---

（2）排序分类

 

---

（3）排序文件的物理表示 —— 数组表示

【算法描述】 

// 定义结构体 RecordType
typedef struct
{
    int key; // 关键字项
    ItemType otheritem; // 其他数据项
} RecordType;

typedef RecordType list[n+1]; // 定义数组类型 list，长度为 n+1

list R; // 定义一个长度为 n+1 的数组 R
R[0], R[1], R[2], ..., R[n]; // 数组 R 的元素

R[i].key; // 第 i 个记录的关键字

【算法详解】

1. 这段代码中，我们首先定义了一个名为 RecordType 的结构体，该结构体包含了两个成员变量：int key（关键字项）和 ItemType otheritem（其他数据项）。
2. 接下来，通过 typedef 关键字，我们将 RecordType 定义为一个新的数组类型 list，该数组的长度为 n+1。
3. 然后，我们声明了一个名为 R 的变量，它是一个长度为 n+1 的 list 类型的数组。这意味着 R 可以存储 n+1 个 RecordType 结构体的实例。数组元素可以通过索引访问，如 R[0]、R[1]、R[2]，一直到 R[n]。
4. 最后，R[i].key 表示访问 R 数组中第 i 个元素的 key 成员变量，即获取第 i 个记录的关键字。
5. 整体上说，该代码段定义了一种数据结构 RecordType，并使用 list 类型的数组 R 来存储多个 RecordType 结构体实例，通过 R[i].key 可以获取指定记录的关键字。

【算法分析】排序指标（排序算法分析）：

• 存储空间
• 比较次数

---

---

二、插入排序（通过比较插入实现排序）

（1）直接插入排序

① 过程

对 R1，…，Ri-1 已排好序，有 K1≤K2≤….≤Ki-1，现将 Ki 依次与 Ki-1，Ki-2，… 进行比较，并移动元素，直到发现 Ri 应插在 Rj 与 Rj+1 之间 (即有 Kj≤Ki＜Kj+1 )，则将 Ri 插到j+1 号位置上，形成 i 个有序序列。 

② 算法

【算法描述】直接插入排序算法： 

void StraightInsertSort(list R, int n)
{
    /*用直接插入排序法对R进行排序*/
    for (int i = 2; i <= n; i++)
    {
        R[0] = R[i];
        int j = i - 1;
        while (R[0].key < R[j].key)
        {
            R[j+1] = R[j]; /*记录后移*/
            j--;
        }
        R[j+1] = R[0]; /*插入*/
    }
}

【算法详解】

1. 这段代码实现了直接插入排序算法，对数组 R 进行排序。
2. 其中，我们使用 for 循环遍历数组 R，从第二个元素开始（i = 2），依次将其插入到已经有序的前面部分。
3. 在内层的 while 循环中，我们通过将记录向后移动来为当前元素寻找合适的插入位置。R[0] 作为哨兵元素，用于保存当前待插入的元素。
4. 在找到合适的位置后，我们将待插入的元素（保存在 R[0] 中）放置到正确的位置上，完成插入操作。
5. 最终，整个数组 R 就按照关键字的非递减顺序进行了排序。

③ 算法分析

• 空间复杂度：O(1)
• 时间复杂度：O(n²)
• 稳定性：稳定排序 

④ 常用的插入排序方法

• 直接插入排序
• 折半插入排序
• 表插入排序
• 希尔排序 

⑤ 示例

 

类似图书馆中整理图书的过程： 

• 记录 R[0] 有两个作用，其一是进入查找循环之前，它保存了 R[i] 的值，使得不致于因记录的后移而丢失 R[i] 中的内容；
• 其二是起岗哨作用，在 while 循环中 “监视” 数组下标变量 j 是否越界，一旦越界 (即 j<1), R[0] 自动控制 while 循环的结束，从而避免了在 while 循环中每一次都要检测 j 是否越界。
• 这一技巧的应用，使得测试循环条件的时间大约减少一半。

---

---

三、交换排序（通过比较交换实现排序）

（1）冒泡排序

① 基本思想

通过多次重复比较、交换相邻记录而实现排序；每一趟的效果都是将当前键值最大的记录

换到最后。  

② 算法

【算法描述】冒泡排序算法： 

void BubbleSort(List R, int n)
{
    /* 用冒泡排序法对R[1]…R[n]进行排序 */
    int i, j, temp, endsort;
    for (i = 1; i <= n - 1; i++)
    {
        endsort = 0; /* 若循环中记录未作交换,则说明序列已有序 */

        for (j = 1; j <= n - i; j++)
        {
            if (R[j].key > R[j + 1].key)
            {
                temp = R[j];
                R[j] = R[j + 1];
                R[j + 1] = temp;
                endsort = 1;
            }
        }

        if (endsort == 0)
            break; /* 已有序，提前结束排序 */
    }
}

【算法详解】

1. 这段代码实现了冒泡排序算法，对数组 R 的元素进行排序。
2. 在外层的 for 循环中，我们要进行 n-1 轮冒泡排序，每轮将一个未排序的最大元素放置到正确的位置上。
3. 在内层的 for 循环中，我们通过比较相邻的元素的关键字，如果前一个元素的关键字大于后一个元素的关键字，就进行交换，以实现升序排序。
4. 若循环中没有进行任何交换操作，即 endsort 保持为 0，则说明整个序列已经有序，提前结束排序。
5. 最终，数组 R 的元素按照关键字的非递减顺序进行了排序。

③ 算法分析

• 时间复杂度：外循环最多 n-1 次（最少 1 次），第 i 次外循环时，内循环 n-i 次比较，所以最大比较次数为：
• 空间复杂度：O(1)
• 稳定性：稳定排序

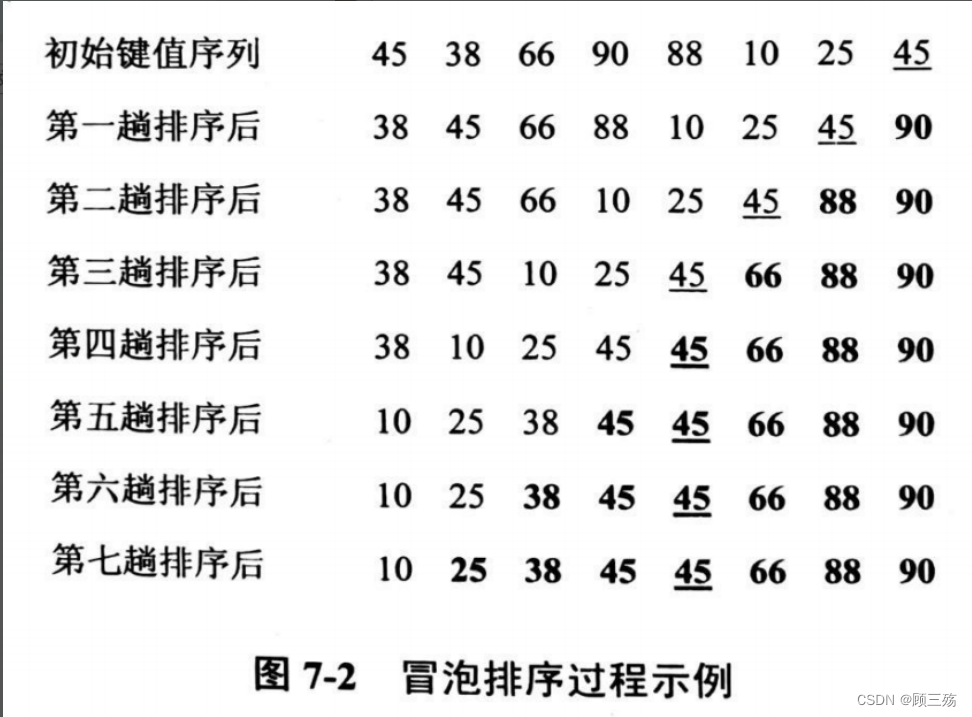
④ 示例

试对下列待排序序列用冒泡排序法进行排序 ， 给出每趟结果 ：

{ 49 ， 38 ， 65 ， 97 ， 76 ， 134 ， 27 ， 49 }

第一趟： 38 49 65 76 97 27 49 [ 134 ]
第二趟： 38 49 65 76 27 49 [ 97 134 ]
第三趟： 38 49 65 27 49 [ 76 97 134 ]
第四趟： 38 49 27 49 [ 65 76 97 134 ]
第五趟： 38 27 49 [ 49 65 76 97 134 ]
第六趟： 27 38 [ 49 49 65 76 97 134 ]
第七趟： 27 [ 38 49 49 65 76 97 134 ]

 

---

（2）快速排序

① 基本思想

• 通过分部排序完成整个表的排序
• 首先取第一个记录，将之与表中其余记录比较并交换，从而将它放到记录的正确的最终位置，使记录表分成两部分 { 其一（左边的）诸记录的关键字均小于它
• 其二 （右边的）诸记录的关键字均大于它 } ；然后对这两部分重新执行上述过程，依此类推，直至排序完毕 

② 过程

• 记录序列： { r[h],r[low+1],…,r[p] }
• 设：左指针 i，右指针 j ;
• 初值：i=h； j=p;  处理元素=>x ;

 

 

此过程直到 (1) 或 (2) 中 i=j 时停止，此时将处理元素 x 送到 i 或 j 位置上，它将原序列分成左、右两个子序列，对 它们分别进行上述过程，直至分裂后的子序列都只有一 个元素为止。

③ 算法

【算法描述】快速排序算法： 

void quickpass(list r, int h, int p)
{
    /* 对顺序表r中的子序列r[h]至r[p]进行快速排序 */
    
    int i = h, j = p; /* 左右指针置初值 */
    ItemType x = r[h]; /* 取处理元素（即作为枢轴记录） */

    while (i < j)
    {
        /* 左右指针未碰头则反复做 */
        while (r[j].key > x.key && i < j)
            --j; /* 右边未找到小关键字，则右指针j继续左移 */

        if (i < j)
        {
            /* 右边找到比枢轴记录小的记录，则将其送到左边 */
            r[i] = r[j];
            ++i;
        }

        while (r[i].key <= x.key && i < j)
            ++i; /* 左边未找到大关键字，则左指针i继续右移 */

        if (i < j)
        {
            /* 左边找到比枢轴记录大的记录，则将其送到右边 */
            r[j] = r[i];
            --j;
        }
    }

    r[i] = x; /* 枢轴记录定位 */

    if (h < i - 1)
        quickpass(r, h, i - 1); /* 对左子序列进行快速排序 */

    if (j + 1 < p)
        quickpass(r, j + 1, p); /* 对右子序列进行快速排序 */
}

【算法详解】

• 这段代码实现了快速排序算法，对顺序表 r 中的子序列 r[h] 至 r[p] 进行排序。
• 在 quickpass 函数内部，我们使用左指针 i 和右指针 j 对子序列进行划分和排序。
• 首先，我们将 r[h] 的值作为枢轴记录，并将左指针 i 置为 h，右指针 j 置为 p。

• 接着，通过循环执行以下步骤：

1. 从右边开始，找到一个关键字小于枢轴记录的元素，并将其移到左边，同时右指针 j 向左移动。
2. 从左边开始，找到一个关键字大于等于枢轴记录的元素，并将其移到右边，同时左指针 i 向右移动。

• 不断进行上述操作，直到左指针 i 和右指针 j 相遇。
• 最后，将枢轴记录（保存在 x 中）放置到相遇位置，将子序列分为左右两个部分。
• 对于左子序列，如果序列长度大于 1，则递归调用 quickpass 函数对其进行快速排序。
• 对于右子序列，如果序列长度大于 1，则递归调用 quickpass 函数对其进行快速排序。
• 通过不断递归和划分子序列，最终整个子序列会按照关键字的非递减顺序进行排序。 

④ 算法分析

1. 空间：O(log₂n)

2. 时间：O(nlog₂n)       最差 O(n²)

• 注：若初始记录表有序或基本有序，则快速排序将蜕化为冒泡排序,其时间复杂度为O(n²)；
• 即：快速排序在表基本有序时，最不利于其发挥效率。

3. 稳定性：不稳定排序

⑤ 示例 

 

 

---

---

四、选择排序（以重复选择的思想为基础进行排序）

（1）直接选择排序

① 过程

设记录 R1，R2…，Rn， 对 i=1，2，…，n-1，重复下列工作：

• 在 Ri，…，Rn 中选最小 (或最大) 关键字记录 Rj
• 将 Rj 与第 i 个记录交换位置，即将选到的第 i 小的记录换到第 i 号位置上 

② 算法

【算法描述】直接选择排序算法： 

void SelectSort(List R, int n)
{
    /* 选择排序算法对顺序表R进行排序 */

    int min, i, j, temp;
    for (i = 1; i <= n - 1; i++)
    {
        min = i; /* 选择第i小的记录，并交换位置 */

        for (j = i + 1; j <= n; j++)
        {
            if (R[j].key < R[min].key)
                min = j; /* 在R[i]...R[n]中找最小者 */
        }

        if (min != i)
        {
            /* 交换记录 */
            temp = R[i];
            R[i] = R[min];
            R[min] = temp;
        }
    }
}

【算法详解】

1. 这段代码实现了选择排序算法，对顺序表 R 进行排序。
2. 在外层的 for 循环中，我们从第一个元素开始，依次选择第 i 小的记录，并将它与第 i 个记录进行交换位置。
3. 在内层的 for 循环中，我们遍历从第 i+1 个位置到最后一个位置的元素，通过比较找到 R[i] 到 R[n] 中的最小者的索引 min。
4. 如果 min 不等于当前的 i，则说明找到了一个更小的元素，我们将这个最小元素与第 i 个元素进行交换，使得最小元素被放置在正确的位置上。
5. 通过进行多次循环，并选择和交换记录的操作，最终整个顺序表 R 的元素会按照关键字的非递减顺序进行排序。 

③ 算法分析

• 空间： O(1)
• 时间：
• 稳定性：不稳定排序 

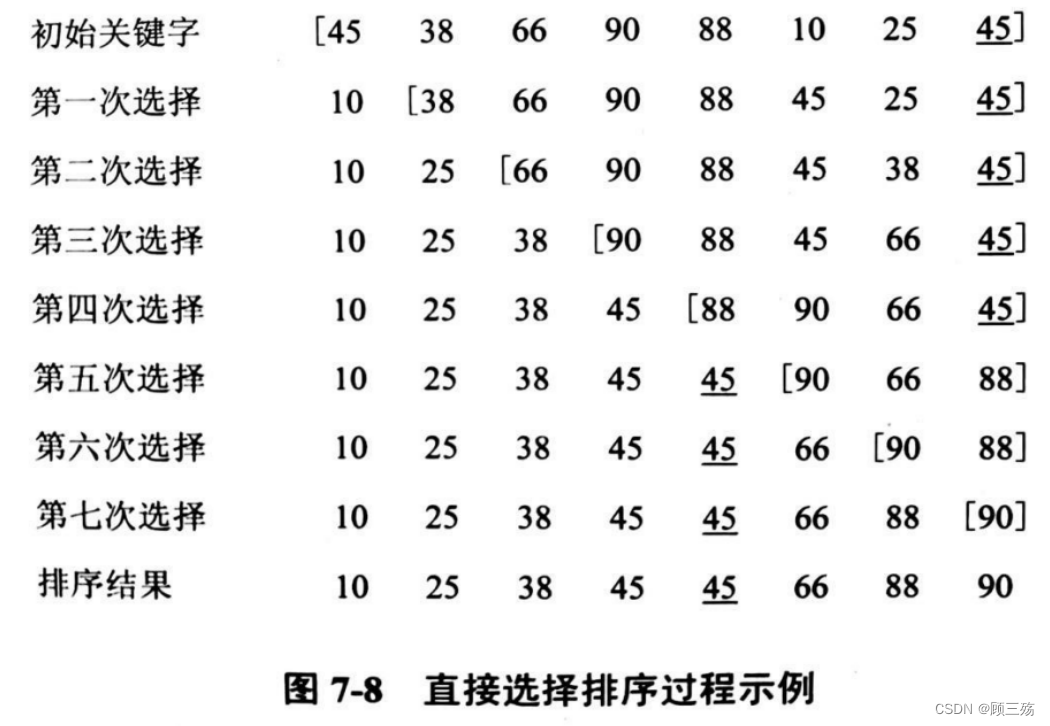
④ 示例

试对下列待排序序列用选择排序法进行排序 , 给出每趟结果 :

{ 46 ， 15 ， 13 ， 94 ， 17}

第一趟： 1 3 [15， 46，94，17]
第二趟： 1 3 15 [ 46，94，17]
第三趟： 1 3 15 17 [ 94，46]
第四趟： 1 3 15 17 46 94

 

---

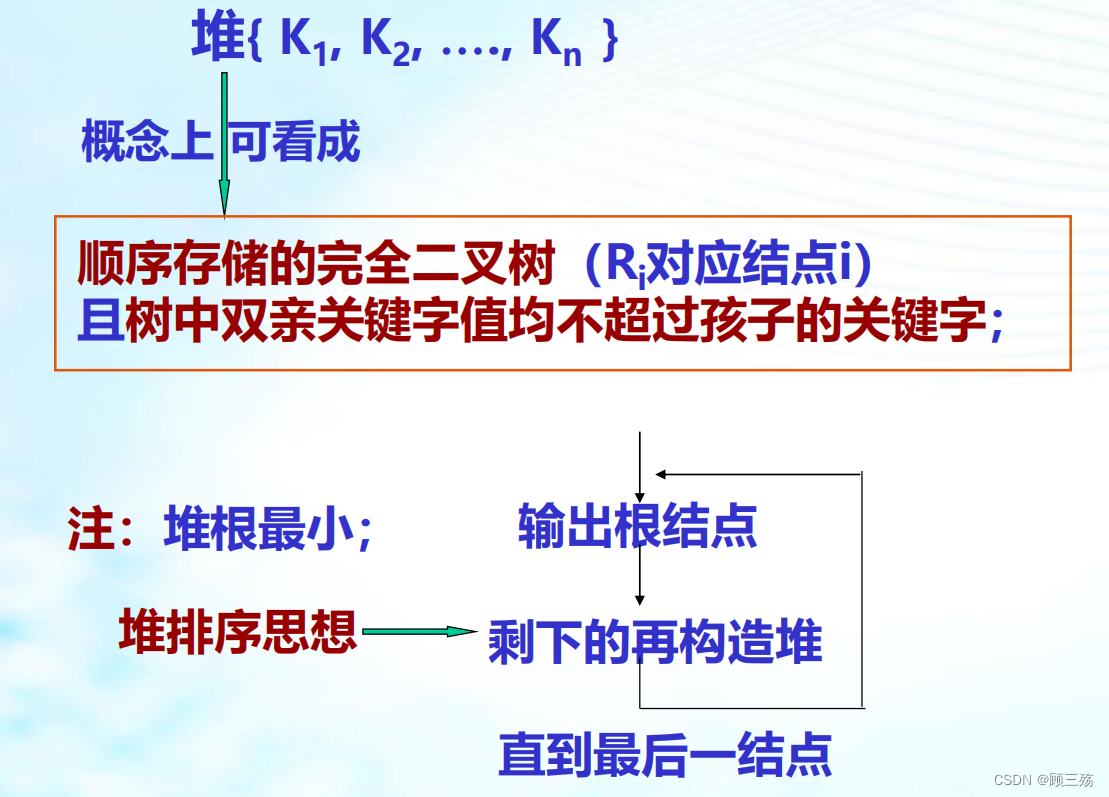
（2）堆排序

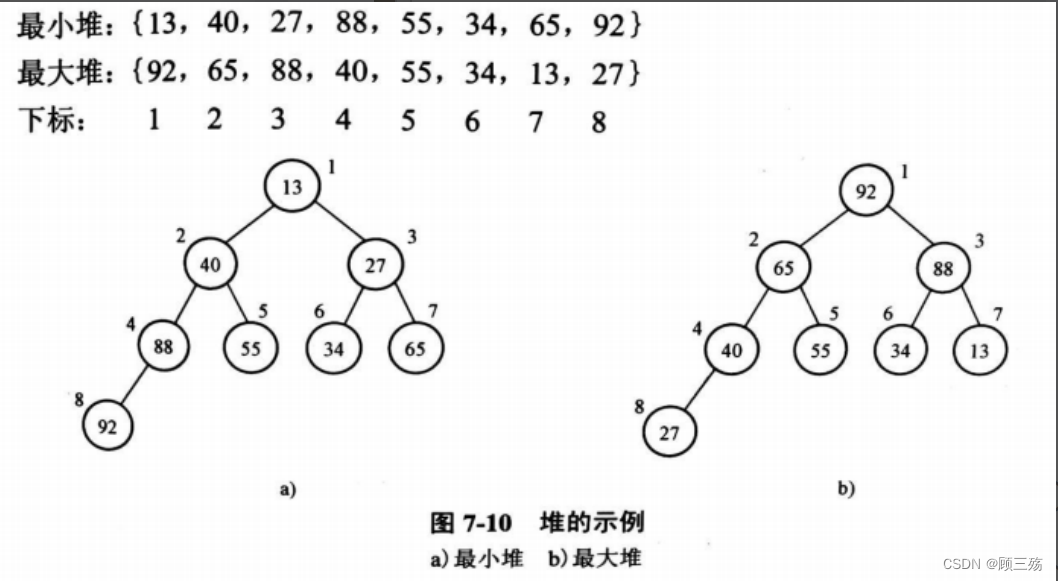
① 堆

【含义】

• 集合 { K1 , K2 , …., Kn }
• 对所有 i=1,2,…,n/2 有： Ki≤K2i 且 Ki≤K2i+1
• 则此集合称为堆（最小堆）
• 或 Ki≥K2i 且 Ki≥K2i+1 最大堆

【示例】

• ｛13,40,27,88,55,34,65,92｝(最小堆)
• ｛92,65,88,40,55,34,13,27｝(最大堆)

【下标】

1 2 3 4 5 6 7 8

【对应的完全二叉树】

【说明】 

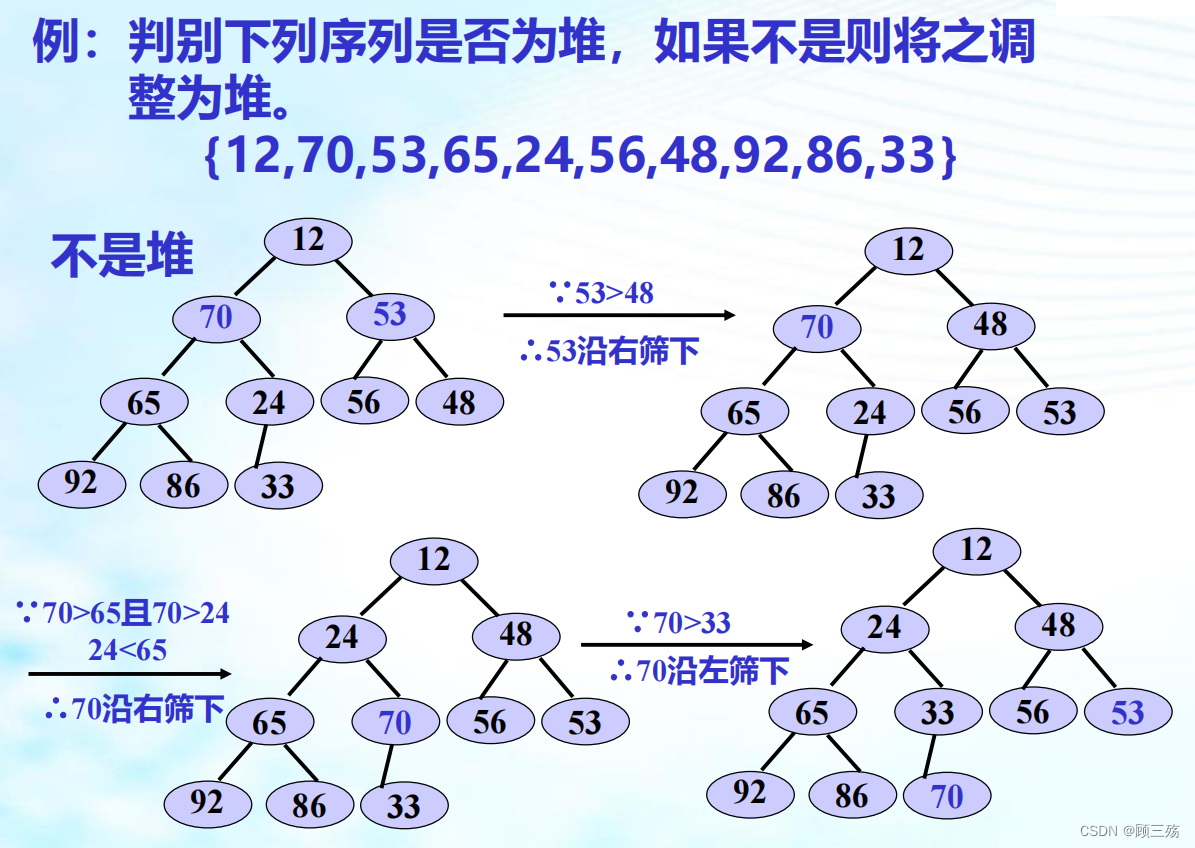
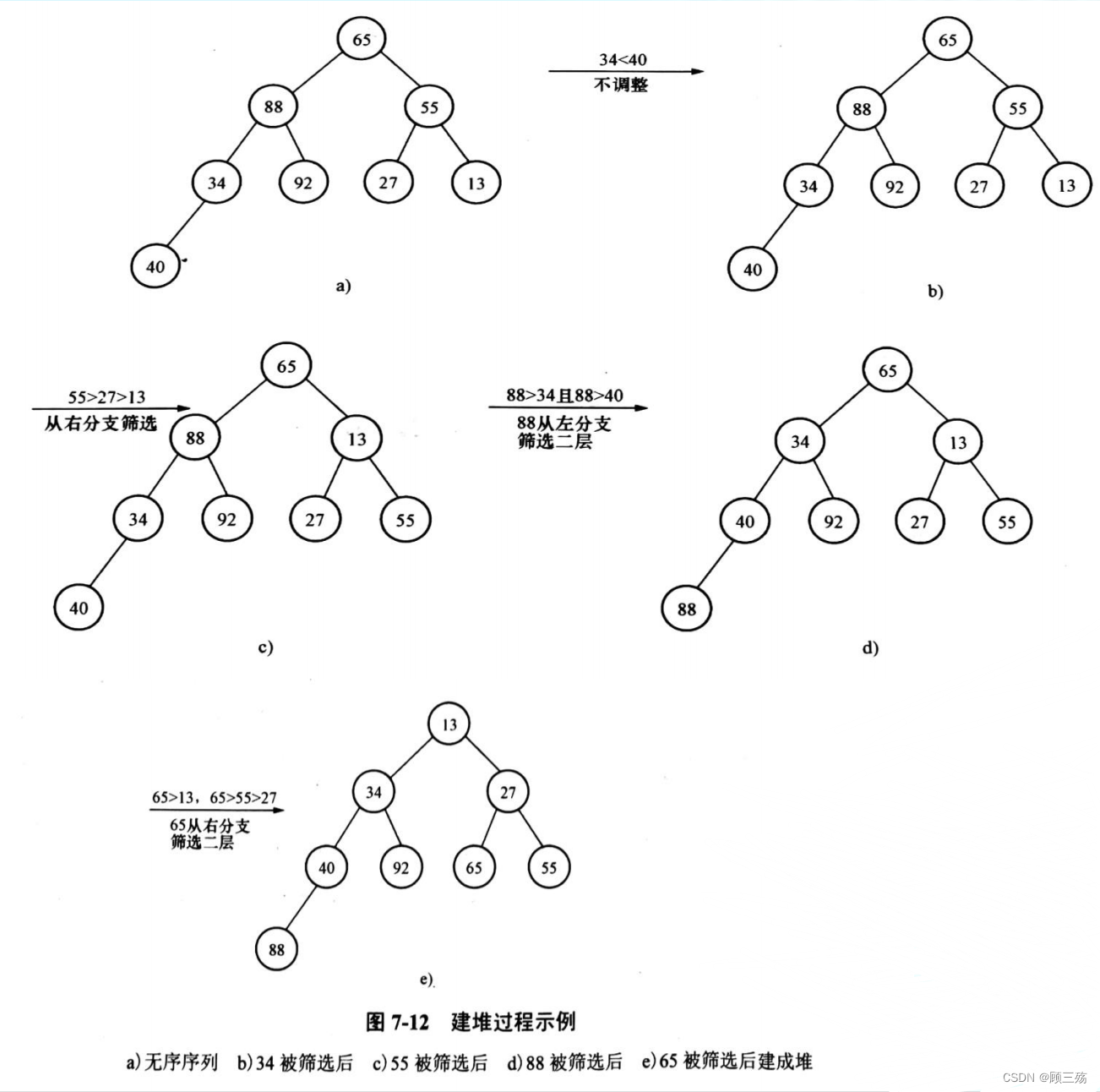
② 建堆（筛选法） 

【方法】 设记录 { R1 , R2 , …., Rn }：

1. 顺序输入成完全二叉树（以数组存储）
2. 从最后一个双亲开始，如果有较小的孩子，则将其沿左或右孩中小的那个方向筛下，一直到不能再筛
3. 逐次处理完每个双亲

【示例】

• 其中 n=8， n/2=4，所以从 k4=34 开始执行。

【算法】 下筛一个结点算法

• 建堆：对k=n/2,…,1依次调用sift

③ 过程

1. 从 i=int(n/2）→ 1 调用 sift(r,i,n) 建初始堆，对 i=n,n-1,n-2,….,2 重复第 2、3 步
2. 输出 r[1]，即：r[1] ← > r[i]
3. 调用 sift(r,1,i-1)，重新建堆 

④ 算法

堆排序是一种基于二叉堆数据结构的排序算法。

它利用了二叉堆的性质，通过将待排序的元素构建成一个最大堆（或最小堆），然后逐步将堆顶元素与堆尾元素交换，并对剩余元素重新进行堆调整，从而实现排序。 

【算法描述】堆排序算法： 

// 将元素arr[i]下沉至适合的位置
void sink(int arr[], int n, int i)
{
    int largest = i; // 初始化堆顶元素
    int left = 2 * i + 1; // 左子节点索引
    int right = 2 * i + 2; // 右子节点索引

    // 找到左右子节点中较大的节点索引
    if (left < n && arr[left] > arr[largest])
        largest = left;
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // 若较大的节点不是当前节点，则交换节点并继续下沉
    if (largest != i)
    {
        swap(arr[i], arr[largest]);
        sink(arr, n, largest);
    }
}

// 堆排序算法
void heapSort(int arr[], int n)
{
    // 构建最大堆
    for (int i = n / 2 - 1; i >= 0; i--)
        sink(arr, n, i);

    // 逐个将堆顶元素与堆尾元素交换，再调整堆
    for (int i = n - 1; i > 0; i--)
    {
        swap(arr[0], arr[i]); // 交换堆顶元素与堆尾元素
        sink(arr, i, 0); // 调整堆
    }
}

【算法详解】

• 这段代码实现了堆排序算法。函数 sink 用于将元素下沉至适合的位置，函数 heapSort 是堆排序的主函数。
• 堆排序的过程如下：

1. 首先，通过循环调用 sink 函数，从最后一个非叶子节点开始构建最大堆。循环条件为 i >= 0，每次减小 i 的值。
2. 构建最大堆之后，将堆顶元素与堆尾元素交换，将最大元素放置在正确的位置上，并缩小堆的范围。
3. 接着，调用 sink 函数对交换后的堆顶元素进行下沉操作，以保证剩余元素仍符合最大堆的性质。
4. 重复步骤 2 和步骤 3 ，直到堆的范围缩小到只有一个元素，排序完成。

• 通过不断地调整堆和交换元素的步骤，堆排序能够将数组按照升序进行排序。 

⑤ 算法分析

• 空间：O(1) （仅需一个记录大小的供交换用的辅助存储空间）
• 时间：O(nlog₂n)
• 稳定性：不稳定排序  

⑥ 示例

 

---

---

五、归并排序

（1）有序序列的合并（两个有序表归并成一个有序表）

① 思想

• 比较各个子序列的第一个记录的键值，最小的一个就是排序后序列的第一个记录。
• 取出这个记录，继续比较各子序列现有的第一个记录的键值，便可找出排序后的第二个记录。
• 如此继续下去，最终可以得到排序结果。  

② 算法（两个有序表归并算法）

有序表归并是将两个有序表合并成一个有序表的算法。 

【算法描述】两个有序表归并算法​​​​​​​： 

def merge(arr1, arr2):
    n1 = len(arr1)  # arr1的长度
    n2 = len(arr2)  # arr2的长度
    merged = []  # 合并后的有序表

    i, j = 0, 0  # i和j分别表示在arr1和arr2中的当前位置

    # 依次比较arr1和arr2中的元素，并将较小的元素添加到merged中
    while i < n1 and j < n2:
        if arr1[i] <= arr2[j]:
            merged.append(arr1[i])
            i += 1
        else:
            merged.append(arr2[j])
            j += 1

    # 将arr1或arr2中剩余的元素添加到merged中
    while i < n1:
        merged.append(arr1[i])
        i += 1
    while j < n2:
        merged.append(arr2[j])
        j += 1

    return merged

【算法详解】

• 这段代码实现了将两个有序表 arr1 和 arr2 进行归并的算法。算法的过程如下：

1. 初始化一个空列表 merged，用于存储合并后的有序表。
2. 使用两个指针 i 和 j 分别指向两个有序表 arr1 和 arr2 的起始位置。
3. 比较 arr1[i] 和 arr2[j] 的大小，将较小的元素添加到 merged 中，并将相应的指针递增。
4. 重复步骤3，直到其中一个有序表的元素全部添加到 merged 中。
5. 将剩余的有序表中的元素依次添加到 merged 的末尾。
6. 返回合并后的有序表 merged。

• 通过将两个有序表逐个比较并添加到合并后的有序表中，最终可以得到一个有序的合并结果。 

---

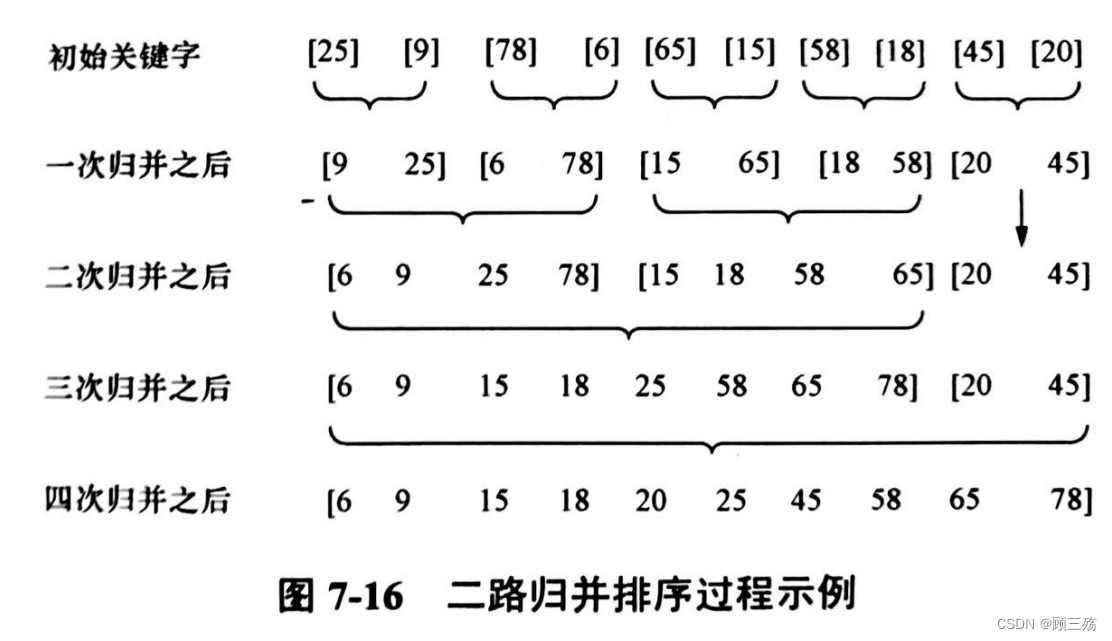
（2）二路归并排序

① 思想 

 

② 算法

【算法描述】二路归并排序​​​​​​​算法： 

void Merge(List a, List R, int h, int m, int n)
{
    /* 将 a[h], ..., a[m] 和 a[m+1], ..., a[n] 两个有序序列合并成一个有序序列 R[h], ..., R[n] */
    
    int k = h, j = m + 1; // k, j 置为序列的起始位置

    while (h <= m && j <= n)
    {
        /* 将 a 中的记录从小到大合并入 R */
        if (a[h].key <= a[j].key)
        {
            /* a[h] 键值小，送入 R[k] 并修改 h 的值 */
            R[k] = a[h];
            h++;
        }
        else
        {
            /* a[j] 键值小，送入 R[k] 并修改 j 的值 */
            R[k] = a[j];
            j++;
        }
        k++;
    }

    while (h <= m)
    {
        /* j > n，将 a[h], ..., a[m] 剩余部分插入 R 的末尾 */
        R[k] = a[h];
        h++;
        k++;
    }

    while (j <= n)
    {
        /* h > m，将 a[m+1], ..., a[n] 剩余部分插入 R 的末尾 */
        R[k] = a[j];
        j++;
        k++;
    }
}

【算法详解】

1. 这段代码实现了将两个有序序列 a[h], …, a[m] 和 a[m+1], …, a[n] 合并成一个有序序列 R[h], …, R[n] 的函数。
2. 在函数中，使用变量 k 和 j 分别表示序列 R 和 a 的起始位置。
3. 首先，在一个循环中，遍历 a[h] 到 a[m] 和 a[m+1] 到 a[n] 的元素，将较小的元素放入 R 中，并相应地递增对应的指针 h 或 j。
4. 然后，在两个单独的循环中，将剩余的元素分别从 a[h] 到 a[m] 和 a[m+1] 到 a[n] 中插入到 R 的末尾，保持有序性。
5. 最终，可以得到一个有序的合并结果 R[h], …, R[n]。 

③ 算法分析

• 空间：O(n)
• 时间：O(nlog₂n)
• 稳定性：稳定排序

④ 示例

试对下列待排序序列用归并排序法进行排序 , 给出每趟结果 :

{ 475 ， 137 ， 481 ， 219 ， 382 ， 674 ， 350 ， 326 ， 815 ， 506 }

第一趟：[137 475] [219 481] [382 674] [326 350] [506 815]
第二趟：[137 219 475 481] [326 350 382 674] [506 815]
第三趟：[137 219 326 350 382 475 481 674] [506 815]
第四趟：[137 219 326 350 382 475 481 506 674 815]

 

---

---

六、各种排序方法的比较