110. 平衡二叉树
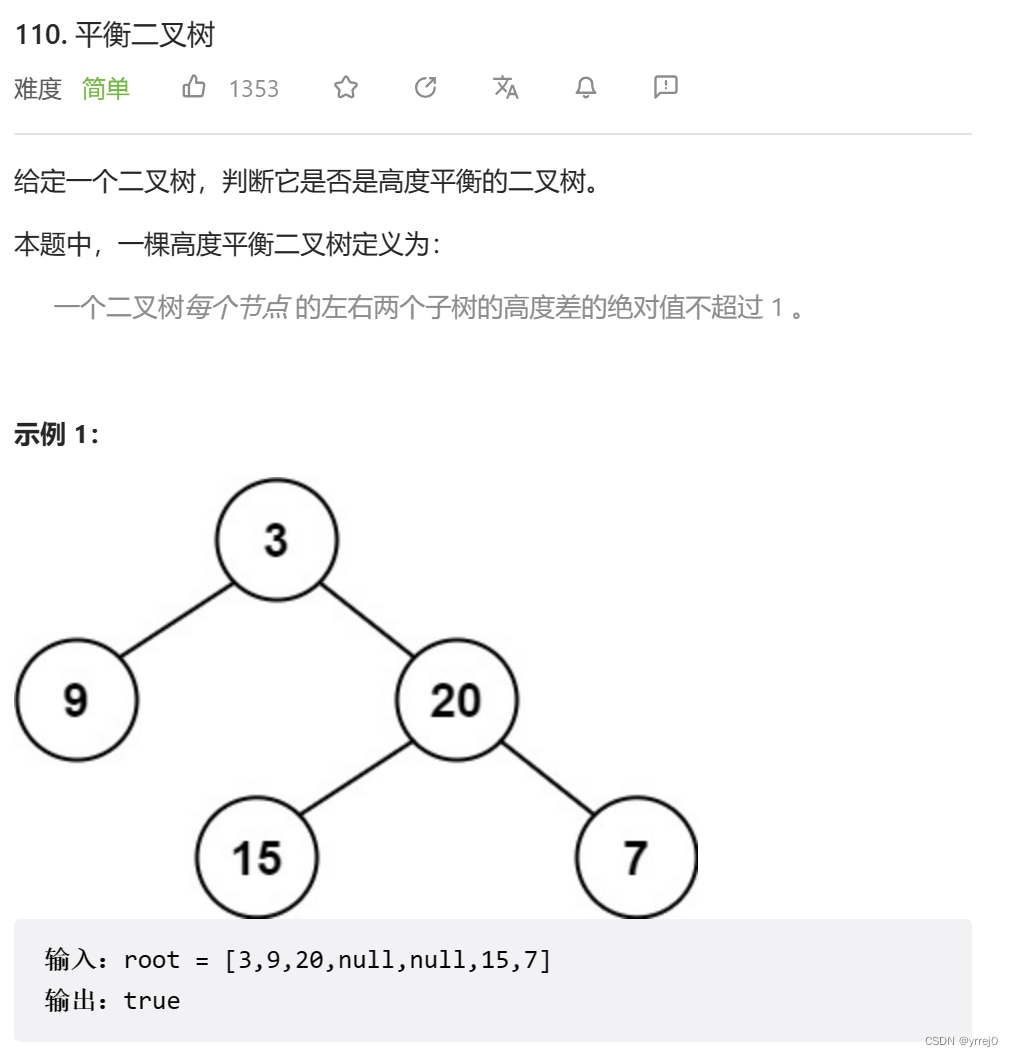
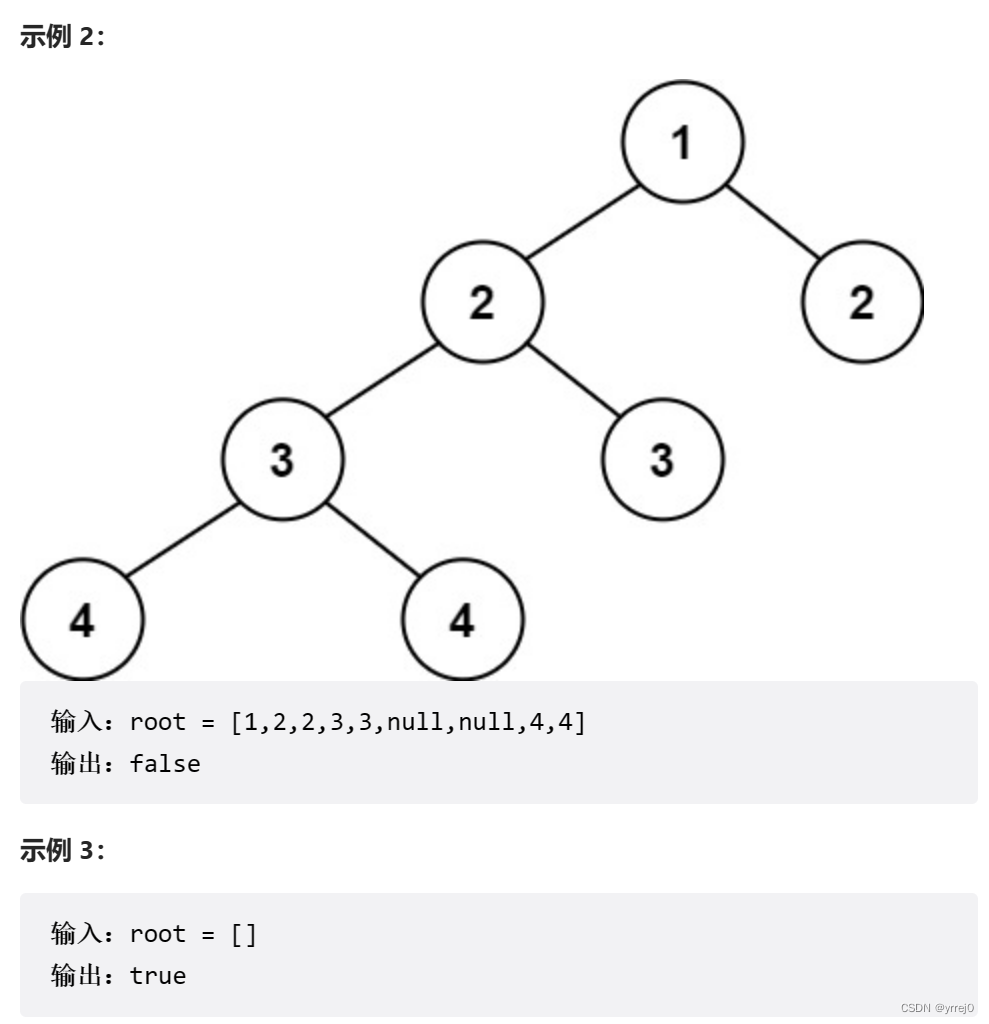
首先是明白什么是平衡二叉树:
一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
然后,区别二叉树的高度和深度:
二叉树的高度:从叶子节点到根节点
二叉树的深度:从根节点到叶子节点
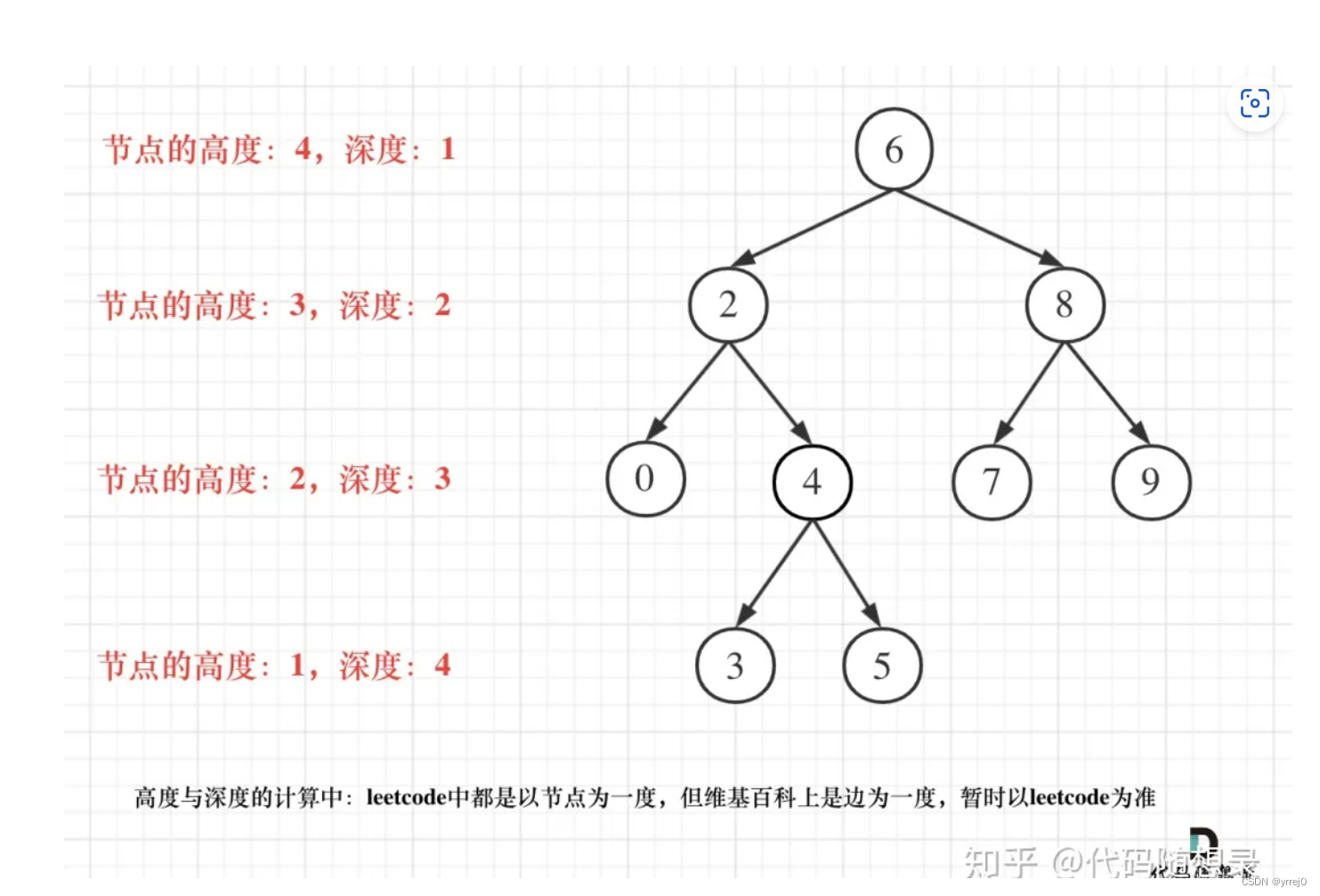
那么对于这道题来说,既然是求高度,那么我们就选择后序遍历的方式,逐渐向上返回子树的高度。可以用-1来标识以当前节点为根节点的左右子树是否为平衡二叉树,如果在过程中有一棵子树的返回值是-1,那么整个树必然不是一个平衡二叉树,如果没有返回-1,那么就正常返回当前树的高度就可以了
代码:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
return self.count_high(root)!=-1
def count_high(self,node):
result = 0
if not node:
return True
left = self.count_high(node.left)
right = self.count_high(node.right)
if left==-1 or right==-1 or abs(left-right)>1:
return -1
return max(left, right) + 1
257. 二叉树的所有路径
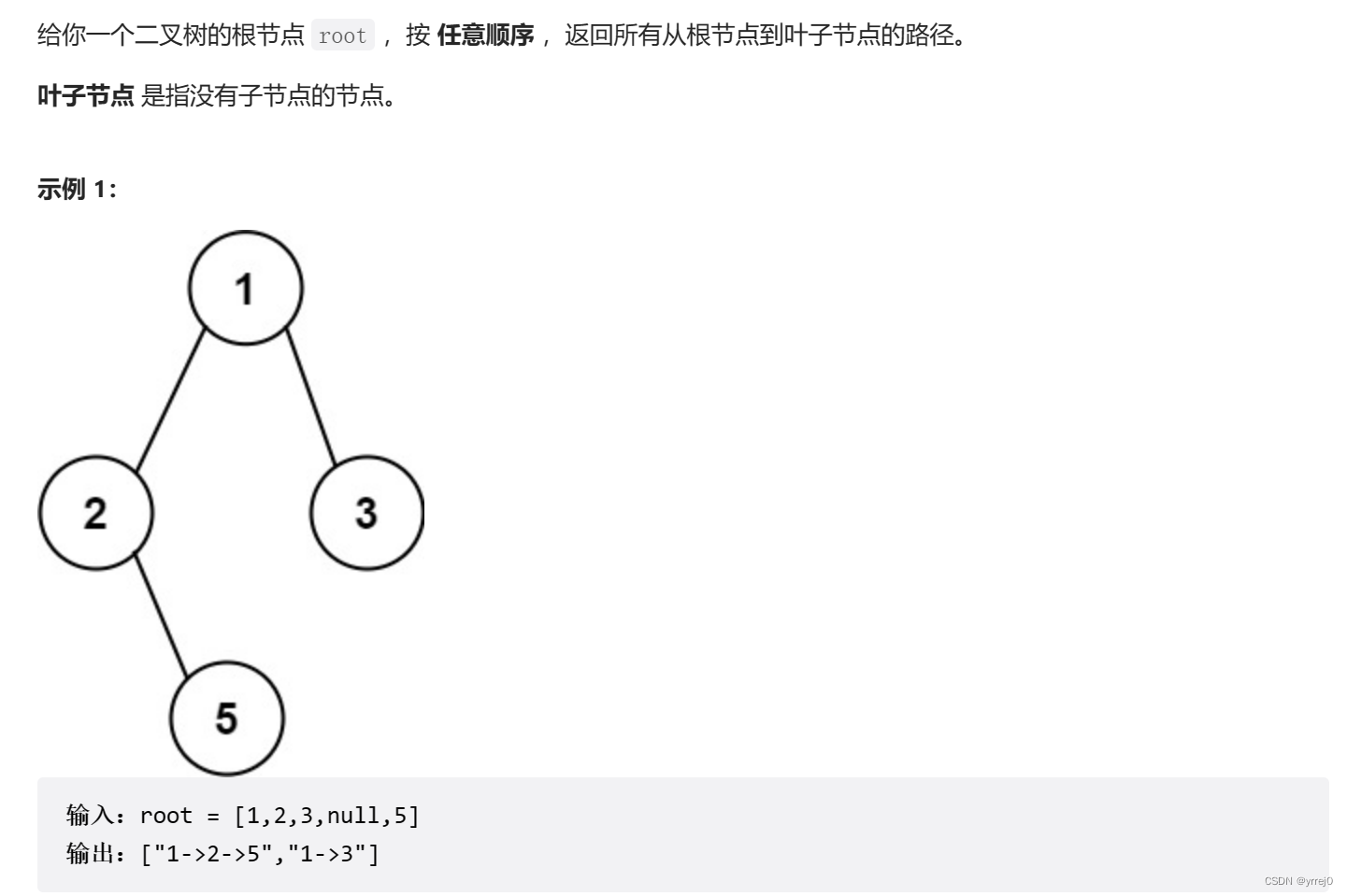

思路:现在开始涉及到一个回溯算法了,首先知道递归和回溯是相辅相成的,有了递归就肯定有回溯。就拿这道题目来说,当从root开始出发,先左子树1->3->5。这是左边的路径保存起来之后,这里就是当我们的左右孩子都为空的时候,说明当前这条路径就已经判断完了,然后就要回到上一个节点,去看他还有没有其他的路径可以继续走,如果还是没有,那么就继续返回上一个节点,直到有新的路径出现为止。
这里稍微注意一下输出格式中有‘->',这里的map函数就是每次保存节点的时候都是以字符形式保存,然后再插入->。
代码:
def traversal(self, cur, path, result):
path.append(cur.val) # 中
if not cur.left and not cur.right: # 到达叶子节点
sPath = '->'.join(map(str, path))
result.append(sPath)
return
if cur.left: # 左
self.traversal(cur.left, path, result)
path.pop() # 回溯
if cur.right: # 右
self.traversal(cur.right, path, result)
path.pop() # 回溯
def binaryTreePaths(self, root):
result = []
path = []
if not root:
return result
self.traversal(root, path, result)
return result404. 左叶子之和
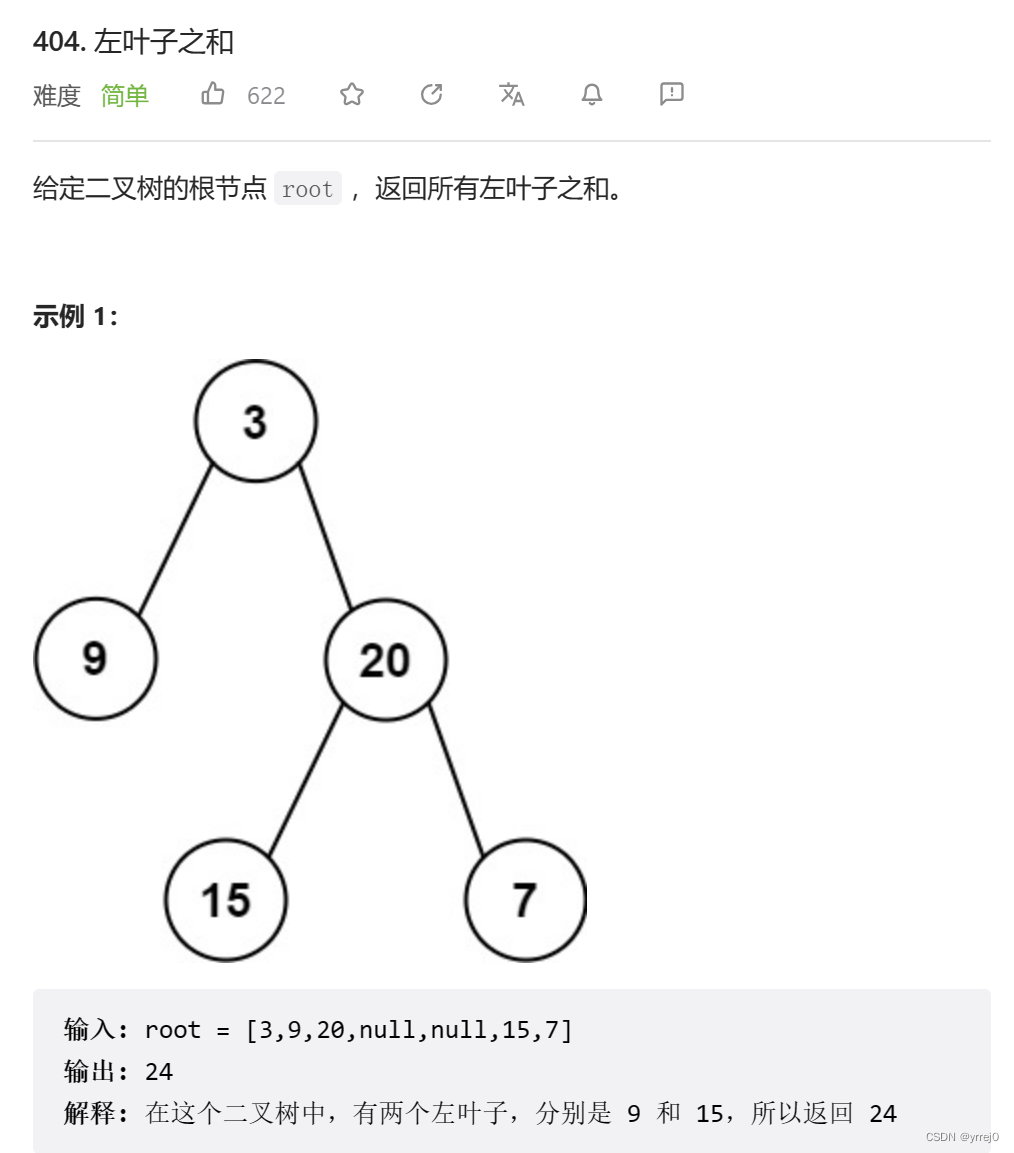

文字游戏来了,什么是叶子节点?就是当前左右孩子都为空。
什么是左叶子节点,就是说当前节点的左孩子不为空,但是左孩子的左右孩子都为空,这就是左叶子节点。那么左边的子树判断完了,就该轮到右子树来了,右子树的左孩子如果既没有左孩子也没有右孩子,那么这也是右子树的左叶子节点。所以递归右子树就好了。
那么如果说当前的左孩子还有孩子,那么就直接分别递归左右子树直到找到他的左右子树的左叶子节点
代码:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
if root.left!=None and root.left.left==None and root.left.right==None:
return root.left.val +self.sumOfLeftLeaves(root.right)
else:
return self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)