提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 第12章 最短路径算法
- 12-1 有权图的最短路径问题
- 最短路径问题-路径规划
- 单源最短路径
- 带权图的最短路径和无权图的最短路径
- 带权图的最短路径算法-Dijkstra算法
- 12-2 Dijkstra 算法的原理和模拟
- 12-3 实现 Dijkstra 算法
- 12-4 Dijkstra 算法的优化
- 12-5 更多关于 Dijkstra 算法的讨论
- 12-7 Bellman-Ford 算法
第12章 最短路径算法
12-1 有权图的最短路径问题
最短路径问题-路径规划
单源最短路径
可以通过广度有限算法或Dijkstra算法,而非深度优先搜索算法
深度优先搜索算法在遍历图时会沿着一个路径一直往下探索,直到无法再继续下去才回溯。这种算法适用于寻找图中的某个目标节点,但不适合求解最短路径问题。因为深度优先搜索算法无法保证找到的路径是最短路径,它可能会陷入一个较长的路径中而错过更短的路径。
相比之下,广度优先搜索算法和迪杰斯特拉算法都可以用于求解单源最短路径问题。广度优先搜索算法通过逐层扩展搜索的方式,从起始节点开始向外层扩展,直到找到目标节点或者遍历完整个图。迪杰斯特拉算法则是一种贪心算法,通过不断更新起始节点到其他节点的最短距离,逐步确定最短路径。
总的来说,如果图中没有边权重(即每条边的权重都相同),那么广度优先搜索算法是一个简单且有效的解决方案。如果图中存在边权重,那么迪杰斯特拉算法是更常用的选择,它可以处理带权重的图,并找到最短路径。
求解到从源点s到图中任意点的最短路径,如果找到了某条路径,那么程序结束。
带权图的最短路径和无权图的最短路径
无权图的最短路径的寻路只需要找到路径数最少的就是解,但是带权图不同
带权图的最短路径算法-Dijkstra算法
Dijkstra算法不能处理负权边
如果要处理负权边,要用其他算法,会使复杂度变高
12-2 Dijkstra 算法的原理和模拟
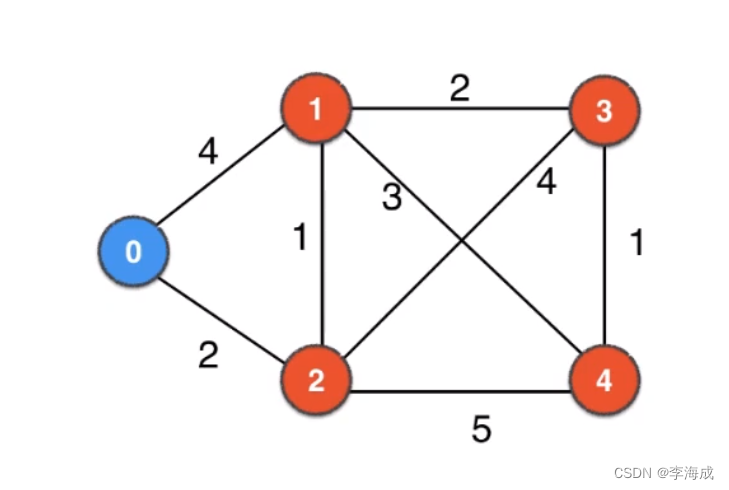
初始化
| dis | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| ∞ | ∞ | ∞ | ∞ | ∞ |
以0为源点,0-0的距离为0,是确定的,用加粗斜体表示,同时由于0-2的距离是所有距离中最小的,也即,即使从0到1然后绕路到2,也无法更小,所以,0-2的距离为2,也是确定的。注意,这里没有负权边。
| dis | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 4 | 2 | ∞ | ∞ |
从2开始可以访问1、3、4,可以更新0到这三个点的距离,同样的道理,0-1的距离被确定了。
| dis | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 3 | 2 | 6 | 7 |
从1出发,访问3、4,可以更新,并确定0-3的距离是5
| dis | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 3 | 2 | 5 | 6 |
最后从3访问4,发现距离还是6,确定0-4距离为6。
| dis | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 3 | 2 | 5 | 6 |
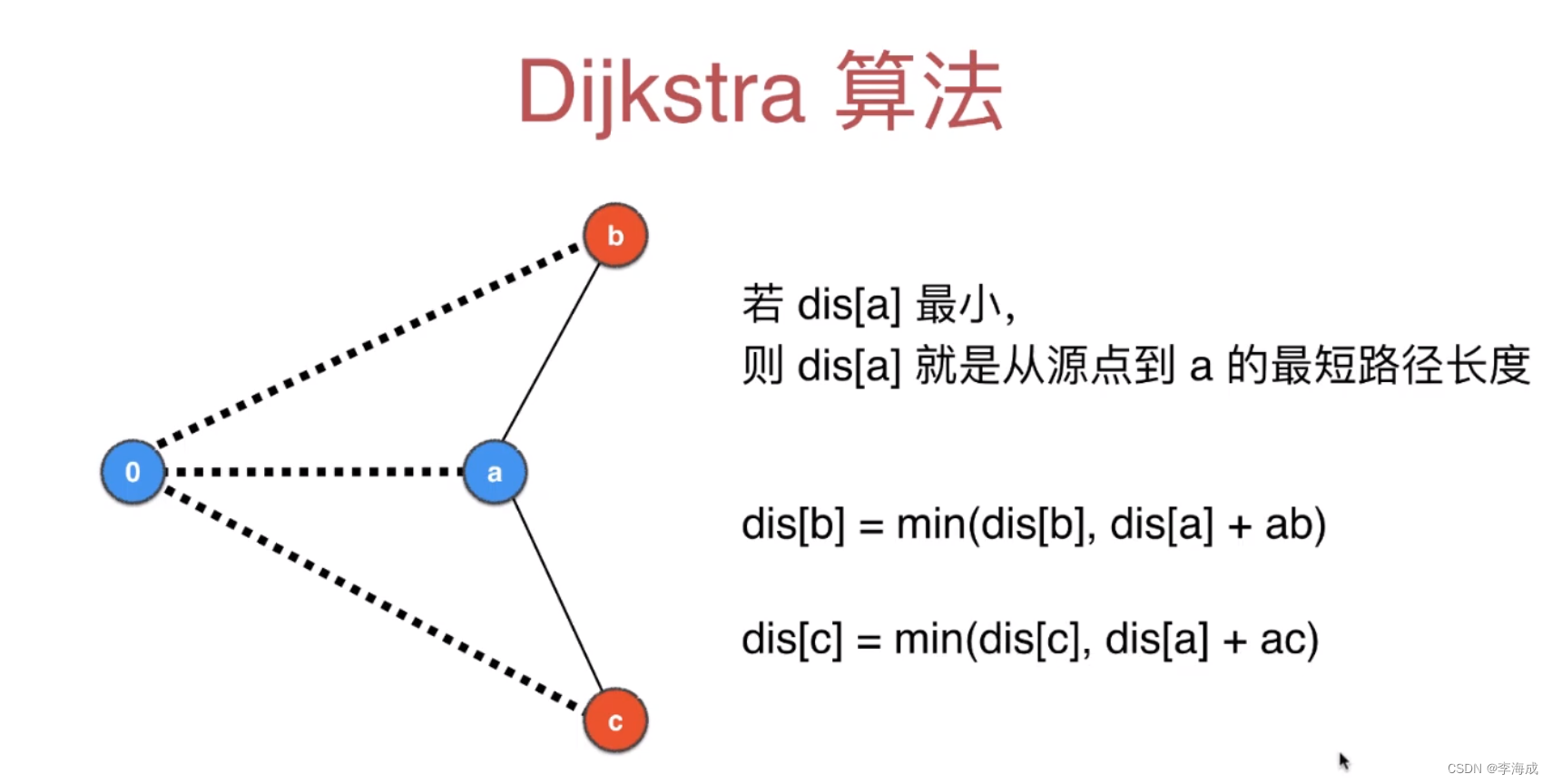
Dijkstra 算法:设置起始源点,将其到自身的距离设为0,然后循环
每轮循环:
- 找到当前没有访问的最短路节点
- 确认这个节点的最段路就是当前大小(注意没有负权边)
- 根据这个节点的最短路大小,更新其他节点的路径长度
图示:
12-3 实现 Dijkstra 算法
以下是使用Go语言实现Dijkstra算法的示例代码:
package main
import (
"fmt"
"math"
)
type Graph struct {
nodes []string
edges map[string]map[string]int
}
func NewGraph() *Graph {
return &Graph{
nodes: []string{},
edges: make(map[string]map[string]int),
}
}
func (g *Graph) AddNode(node string) {
g.nodes = append(g.nodes, node)
}
func (g *Graph) AddEdge(src, dest string, weight int) {
if _, ok := g.edges[src]; !ok {
g.edges[src] = make(map[string]int)
}
g.edges[src][dest] = weight
}
func Dijkstra(graph *Graph, start string) map[string]int {
distances := make(map[string]int) // distances用于存储从起始节点到各个节点的当前最短距离,
visited := make(map[string]bool) // visited用于记录已经访问过的节点。
for _, node := range graph.nodes {
distances[node] = math.MaxInt32 //循环遍历所有节点,并将其初始距离设置为无穷大(math.MaxInt32),
}
distances[start] = 0 // 除了起始节点的距离设置为0。
for i := 0; i < len(graph.nodes); i++ {
current := minDistance(distances, visited) // 选择当前未访问的最短距离的节点作为当前节点,
visited[current] = true // 并将其标记为已访问。
// 遍历当前节点的邻居节点,并更新它们的最短距离。如果通过当前节点到达邻居节点的路径比已知的最短距离更短,则更新邻居节点的最短距离。
for neighbor, weight := range graph.edges[current] {
if !visited[neighbor] && distances[current]+weight < distances[neighbor] {
distances[neighbor] = distances[current] + weight
}
}
}
return distances
}
func minDistance(distances map[string]int, visited map[string]bool) string {
min := math.MaxInt32
var minNode string
for node, distance := range distances {
if !visited[node] && distance < min {
min = distance
minNode = node
}
}
return minNode
}
func main() {
graph := NewGraph()
graph.AddNode("A")
graph.AddNode("B")
graph.AddNode("C")
graph.AddNode("D")
graph.AddNode("E")
graph.AddEdge("A", "B", 4)
graph.AddEdge("A", "C", 2)
graph.AddEdge("B", "C", 1)
graph.AddEdge("B", "D", 5)
graph.AddEdge("C", "D", 8)
graph.AddEdge("C", "E", 10)
graph.AddEdge("D", "E", 2)
distances := Dijkstra(graph, "A")
fmt.Println("Shortest distances from node A:")
for node, distance := range distances {
fmt.Printf("Node: %s, Distance: %d\n", node, distance)
}
}
这个示例代码创建了一个Graph结构体来表示图,其中包含节点和边的信息。然后,通过AddNode和AddEdge方法添加节点和边的权重。最后,调用Dijkstra函数传入图和起始节点来计算最短路径。
在Dijkstra函数中,首先初始化距离数组distances和访问标记visited。然后,使用循环选择当前未访问的最短路径节点,并更新与其相邻节点的距离。最后,返回最短路径距离的映射。
运行上述代码将输出从节点A开始的最短距离结果。
12-4 Dijkstra 算法的优化
12-5 更多关于 Dijkstra 算法的讨论
如果只考虑两个点,那么只要确定了两点的最短路径就可以停止了。
12-7 Bellman-Ford 算法
用于处理有负权边的情况。