最近我在思考为什么： 为什么随机过程的自相关函数和其功率谱密度是一对傅里叶变换？

1、自相关函数和卷积

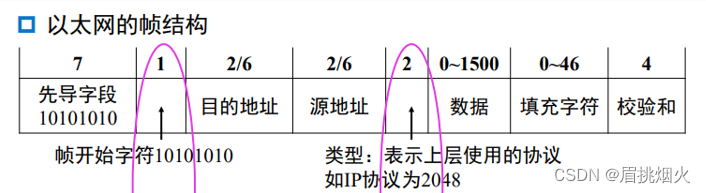
这俩跟孪生兄弟似的，经常一起出现，我们先来看看自相关函数和卷积的定义（谁能教我一下，怎么去除图片里的水印）：

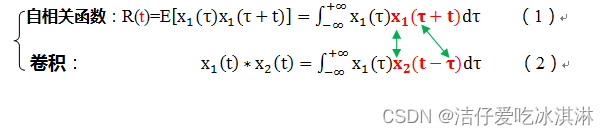
对比一下就会发现：两个公式及其相似。只要把x₂换成x₁，+τ换成-τ即可。那么自相关函数就变成了x₁(t) *x₁(-t)

暂停一下，直观的分析一下两者的关系。
卷积：翻转、平移、乘积
自相关：平移、乘积

发现了吗？两者只差一个翻转（沿时间轴的折叠）。——真是一个惊人的巧合。

说到自相关函数，这里推荐一篇极好的文章自相关函数的理解，里面对自相关函数概念的引出做了很好的诠释.

在这里我简要叙述结论：

1、自相关函数能够表示随机过程样本函数变化的剧烈程度。

2、更重要的，在对随机过程的研究，发现很多统计特性量都与自相关函数有关，只要通过实验方法能够测试得到随机过程的自相关函数，再结合期望、方差就可以进一步推导得到其他统计量。比如：自相关函数的傅里叶变换就是功率谱密度。

2、自相关函数的傅里叶变换

既然自相关函数和卷积存在这样的关系，那我们对x₁(t) *x₁(-t)做傅里叶变换：

到这里，进入第二个重要的节点：


如果直接对自相关函数做傅里叶变换呢？

同（3）式完全一致。因为两者在时域上完全一样，因此进行傅里叶变换后，也肯定是一样的。

那么为什么X(-jω)∙X(jω)就是功率谱呢?

如果x(t)是实信号，X(jω)=R(ω)+jX(ω)，那么有X(jω)的实部是偶函数，虚部是奇函数

所以，X(-jω)=R(-ω)+jX(-ω)=R(ω)-jX(ω)

∴X(jω)X(-jω)=|R(ω) |²+|X(ω)|²=|X(jω) |²

这不就和功率谱联系起来了吗!!

可是如果x(t)不是实信号呢？难道自相关函数的傅里叶变换就不是功率谱密度了？找遍了所有的教科书，没有一本书加了实信号这个限定条件。

那么问题出现在哪里呢？

——出在最最开始的时候，我对自相关函数的定义，只有实信号才是上述定义。

而更广义的定义是：

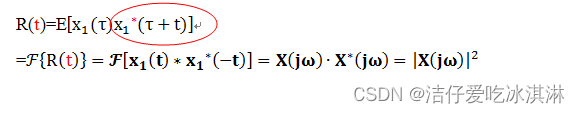
所以，自相关函数←→功率谱密度 是一对傅里叶变换对
！！！没有任何限定条件！！！

那么问题来了，为什么在相关函数的定义中，出现了共轭运算呢？类似的还有——内积。

我认为：所有需要引入共轭运算的，一定都是与能量相关的量（不一定正确哈）

好了，我们继续聊相关函数

其实，函数(信号)的相关运算就是：引入时移因子τ的内积。（把这句话读三遍）函数的内积不考虑时间轴对的准不准的问题，换句话说函数（信号）的内积是相关函数在某点的取值。

之前说过，几何里的内积就是投影，函数里的相关就是以一个函数为基准，另一个函数的“投影”。sin和cos是正交的，内积为0，但如果将sin延迟T/4，那么内积最大。相关运算就是引入时延因子的内积。通信里，匹配滤波器就是类似的原理

上面的推导都是基于确知信号的进行分析的，根据维纳辛欣定理，同样满足：自相关函数←→功率谱密度