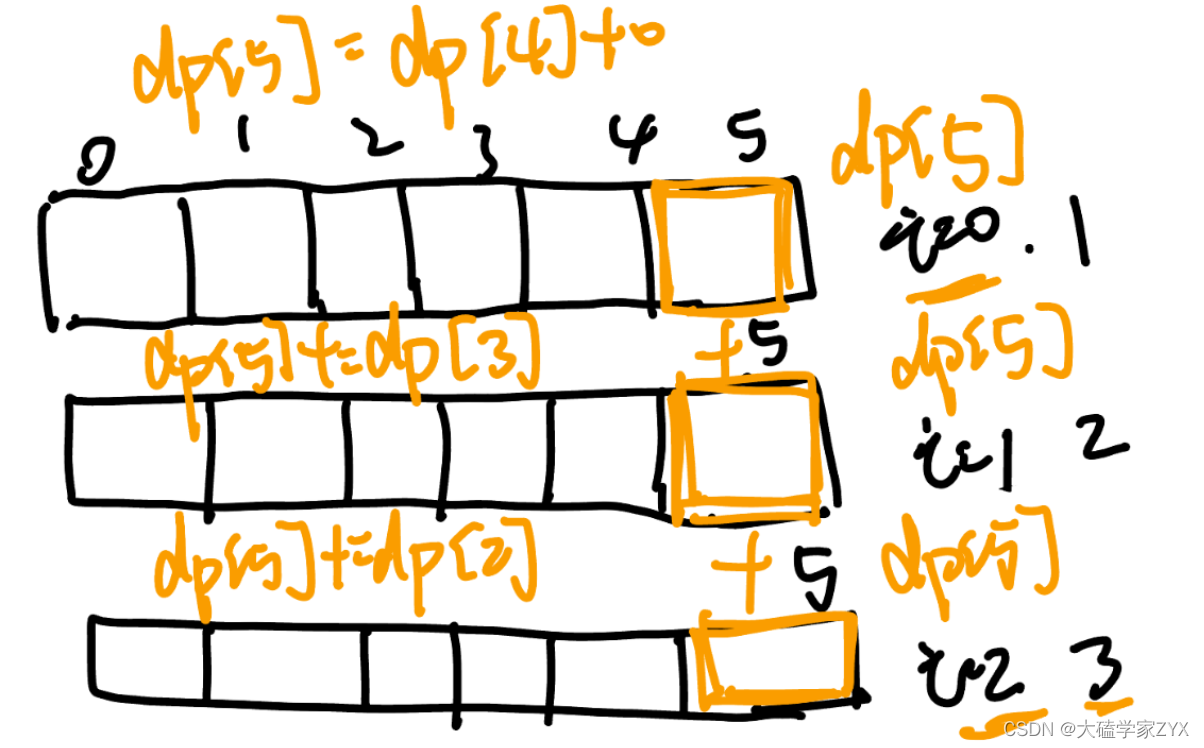
离散化的本质：是建立了一段数列到自然数之间的映射关系（value -> index)，通过建立新索引，来缩小目标区间，使得可以进行一系列连续数组可以进行的操作比如二分，前缀和等…

相应的算法模板：

    vector<int> alls; // 存储所有待离散化的值
    sort(alls.begin(), alls.end()); // 将所有值排序
    alls.erase(unique(alls.begin(), alls.end()), alls.end());    // 去掉重复元素
    
    // 二分求出x对应的离散化的值
    int find(int x)
    {
        int l = 0, r = alls.size() - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (alls[mid] >= x) r = mid;
            else l = mid + 1;
        }
        return r + 1;
    }

题目：

 

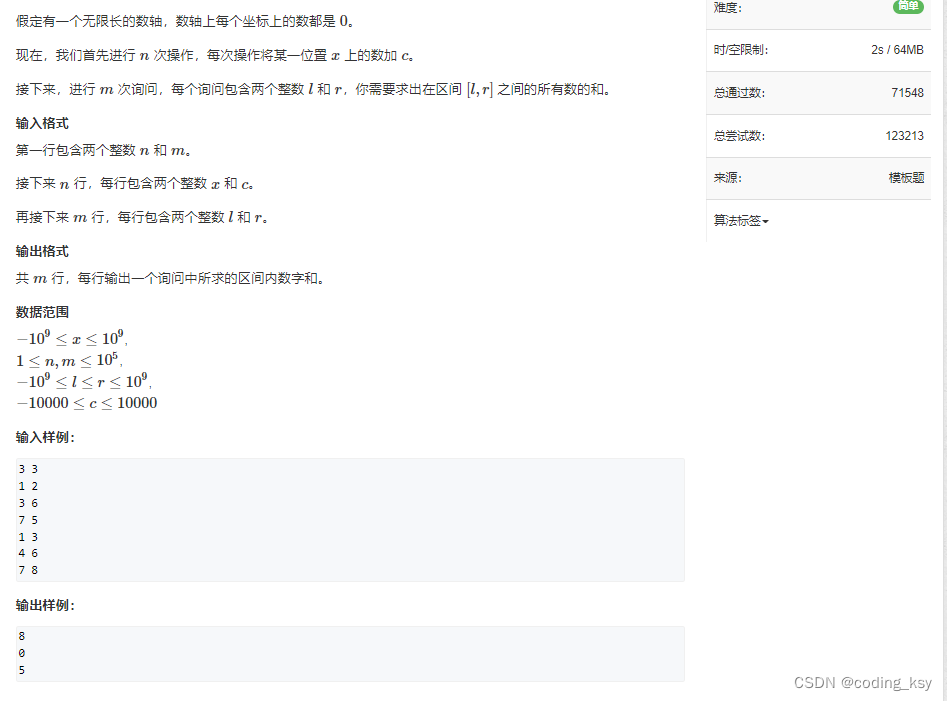
离散化首先需要排序去重：

1. 排序：sort(alls.begin(),alls.end())
2. 去重：alls.earse(unique(alls.begin(),alls.end()),alls.end());

unique()函数的底层原理

vector<int>::iterator unique(vector<int> &a) {
    int j = 0;
    for (int i = 0; i < a.size(); ++i) {
        if (!i || a[i] != a[i - 1])//如果是第一个元素或者该元素不等于前一个元素，即不重复元素，我们就把它存到数组前j个元素中
            a[j++] = a[i];//每存在一个不同元素，j++
    }
    return a.begin() + j;//返回的是前j个不重复元素的下标
}

由于本题可能有多组数据是针对同一个数组下标操作的，因此我们可以将所有用到的数组下标装在一个下标容器alls内去重，然后再逐一为相同的数组下标增加数值c，再通过对应前缀和相减求得区间 l~r 之间的数的值

代码详解：

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

typedef pair<int,int> PII;

const int N = 300010;

int n,m;
int a[N],s[N];


vector<int> alls;//存入下标的容器
vector<PII> add,query;//add增加容器，存入对应下标和增加值的大小
//query存入需要计算下标区间和的容器

int find(int x){
    int l = 0,r = alls.size() - 1;
    while(l < r){
        int mid = l + r >> 1;
        if(alls[mid] >= x){
            r = mid;
        }
        else{
            l = mid + 1;
        }
    }
    
    return r + 1;//因为要使用前缀和，其下标要+1可以不考虑边界问题
    
}


int main(){
    cin >> n >> m;
    for(int i = 0;i < n;i ++ ){
        int x,c;
        cin>> x >> c;
        add.push_back({x,c});//存入下标以及对应的数值c
        
        alls.push_back(x);//存入数组的下标x = add.first
        
    }
  
    for(int i = 0;i < m;i ++ ){
         int l,r;
         cin >> l >> r;
         query.push_back({l,r});
         
         alls.push_back(l);//存入区间的左右下标
         alls.push_back(r);
         
}

//区间去重
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());



//处理插入
for(auto item : add){
    int x = find(item.first);//将add容器的add.secend值存入数组a[]当中
    a[x] += item.second;//在去重之后的下标集合alls内寻找对应的下标并添加数值
}

//预处理前缀和
for(int i = 1;i <= alls.size();i ++ ) s[i] = s[i - 1] + a[i];

//处理查询
for(auto item : query){
    int l = find(item.first) , r = find(item.second);//在下标容器中查找对应的左右两端[l~r]下标，然后通过下标得到前缀和相减再得到区间a[l~r]的和
    cout << s[r] - s[l - 1] << endl;
}

 return 0;
}